一、说明
二、张量的基本概念
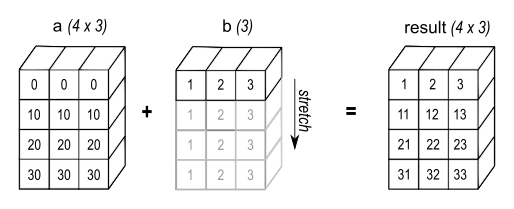
广播可以成为执行张量运算而不创建重复数据的有效方法。
根据 PyTorch 的说法,在以下情况下,张量是“可广播的”:
每个张量至少有一个维度
循环访问维度大小时,从尾随维度开始,维度大小必须相等、其中一个为 1,或者其中一个不存在
比较形状时,尾随维度是最右边的数字。
在上图中,可以看到通用过程:
1. 确定最右侧的尺寸是否兼容
- 每个张量是否至少有一个维度?
- 大小相等吗?其中之一吗?一个不存在吗?
2. 将尺寸拉伸到适当的尺寸
3. 对下一个维度重复上述步骤
这些步骤可以在下面的示例中看到。
三、元素级操作
所有元素级运算都要求张量具有相同的形状。
3.1 矢量和标量示例
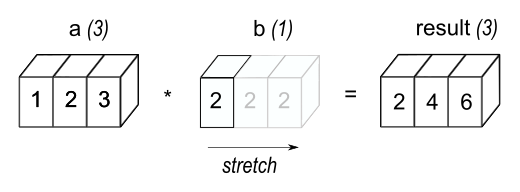
import torch
a = torch.tensor([1, 2, 3])
b = 2 # becomes ([2, 2, 2])a * btensor([2, 4, 6])在此示例中,标量的形状为 (1,),矢量的形状为 (3,)。如图所示,b被广播为(3,)的形状,并且Hadamard乘积按预期执行。
3.2 矩阵和矢量示例 1

在此示例中,A 的形状为 (3, 3),b 的形状为 (3,)。
发生乘法时,向量被逐行拉伸以创建一个矩阵,如上图所示。现在,A 和 b 的形状均为 (3, 3)。
这可以在下面看到。
A = torch.tensor([[1, 2, 3],[4, 5, 6],[7, 8, 9]])b = torch.tensor([1, 2, 3])A * btensor([[ 1, 4, 9],[ 4, 10, 18],[ 7, 16, 27]])3.3 矩阵和矢量示例 2
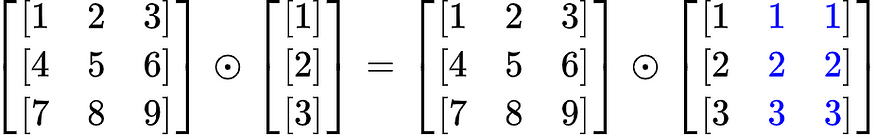
在此示例中,A 的形状为 (3, 3),b 的形状为 (3, 1)。
发生乘法时,向量将逐列拉伸以创建两个额外的列,如上图所示。现在,A 和 b 的形状均为 (3, 3)。
A = torch.tensor([[1, 2, 3],[4, 5, 6],[7, 8, 9]])b = torch.tensor([[1], [2], [3]])
A * btensor([[ 1, 2, 3],[ 8, 10, 12],[21, 24, 27]])Tensor and Vector Example
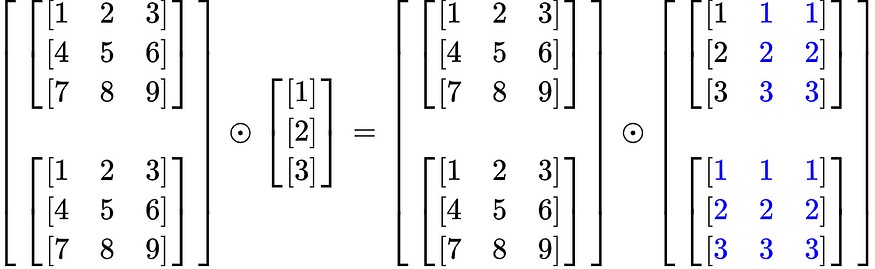
在此示例中,A 是形状为 (2, 3, 3) 的张量,b 是形状为 (3, 1) 的列向量。
A = (2, 3, 3)
b = ( , 3, 1)从最右边的维度开始,每个元素按列拉伸以生成 (3, 3) 矩阵。中间维度相等。在这一点上,b只是一个矩阵。最左侧的维度不存在,因此必须添加一个维度。然后,必须广播矩阵以创建 (2, 3, 3) 的大小。现在有两个 (3, 3) 个矩阵,可以在上图中看到。
这允许计算 Hadamard 乘积并生成 (2, 3, 3) 矩阵:
A = torch.tensor([[[1, 2, 3],[4, 5, 6],[7, 8, 9]],[[1, 2, 3],[4, 5, 6],[7, 8, 9]]])b = torch.tensor([[1], [2], [3]])A * btensor([[[ 1, 2, 3],[ 8, 10, 12],[21, 24, 27]],[[ 1, 2, 3],[ 8, 10, 12],[21, 24, 27]]])3.4 张量和矩阵示例
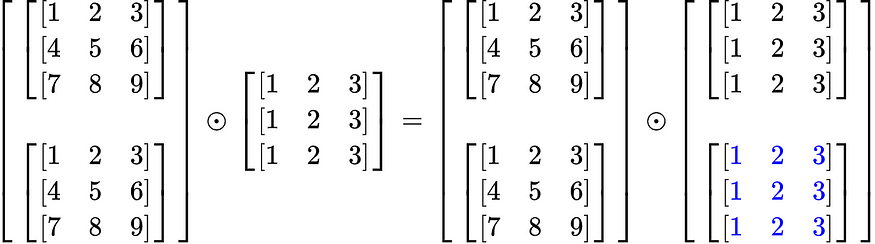
在此示例中,A 是形状为 (2, 3, 3) 的张量,B 是形状为 (3, 3) 的矩阵。
A = (2, 3, 3)
B = ( , 3, 3)此示例比上一个示例更容易,因为最右侧的两个维度是相同的。这意味着矩阵只需在最左侧的维度上广播即可创建 (2, 3, 3) 的形状。这只是意味着需要一个额外的矩阵。
计算哈达玛乘积时,结果为 (2, 3, 3)。
A = torch.tensor([[[1, 2, 3],[4, 5, 6],[7, 8, 9]],[[1, 2, 3],[4, 5, 6],[7, 8, 9]]])B = torch.tensor([[1, 2, 3], [1, 2, 3], [1, 2, 3]])A * Btensor([[[ 1, 4, 9],[ 4, 10, 18],[ 7, 16, 27]],[[ 1, 4, 9],[ 4, 10, 18],[ 7, 16, 27]]])四、矩阵和张量乘法与点积
对于前面的所有示例,目标是以相同的形状结束,以允许逐元素乘法。此示例的目标是通过点积实现矩阵和张量乘法,这需要第一个矩阵或张量的最后一个维度与第二个矩阵或张量的倒数第二个维度匹配。
对于矩阵乘法:
- (m, n) x (n, r) = (c, m, r)
对于 3D 张量乘法:
- (c, m, n) x (c, n, r) = (c, m, r)
对于 4D 张量乘法:
- (z, c, m, n) x (z, c, n, r) = (z, c, m, r)
例
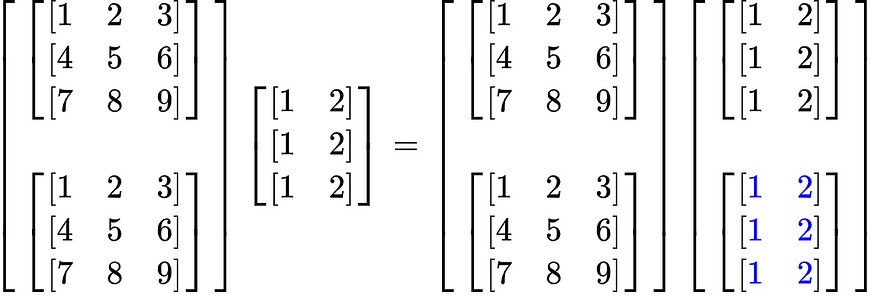
对于此示例,A 的形状为 (2, 3, 3),B 的形状为 (3, 2)。截至目前,最后两个维度符合点积乘法的条件。需要将维度添加到 B,并且需要跨此维度广播 (3, 2) 矩阵以创建 (2, 3, 2) 的形状。
此张量乘法的结果将是 (2, 3, 3) x (2, 3, 2) = (2, 3, 2)。
A = torch.tensor([[[1, 2, 3],[4, 5, 6],[7, 8, 9]],[[1, 2, 3],[4, 5, 6],[7, 8, 9]]])B = torch.tensor([[1, 2], [1, 2], [1, 2]])A @ B # A.matmul(B)tensor([[[ 6, 12],[15, 30],[24, 48]],[[ 6, 12],[15, 30],[24, 48]]])有关广播的其他信息可以在下面的链接中找到。有关张量及其操作的更多信息可以在此处找到。