目录
简单的扩展到泊松分布
比较整体的动态过程,增加实验次数时
当二项分布,n很大,p很小的时候,会趋向泊松分布
当n足够大时,二项分布趋向于正态分布。这个结论在概率论中被称为中心极限定理,它是概率论中一个非常重要的定理,广泛应用于各种领域,如金融、工程、生物学等。
简单的扩展到泊松分布
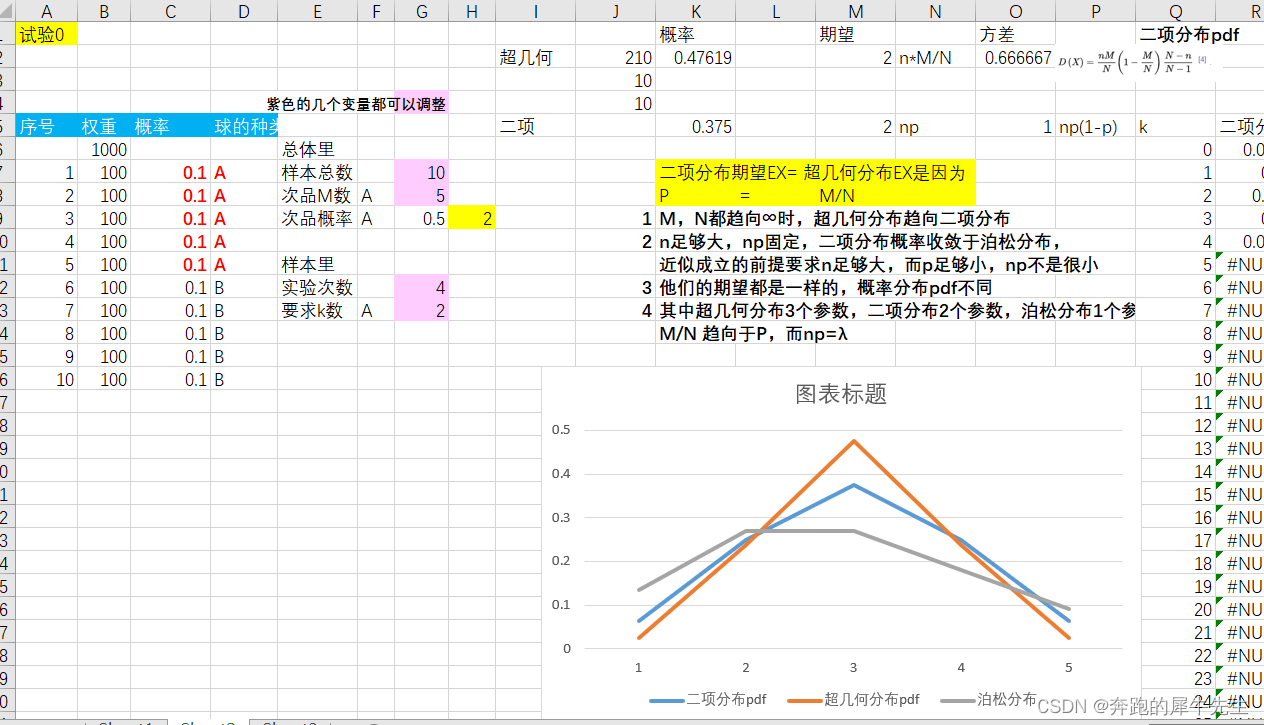
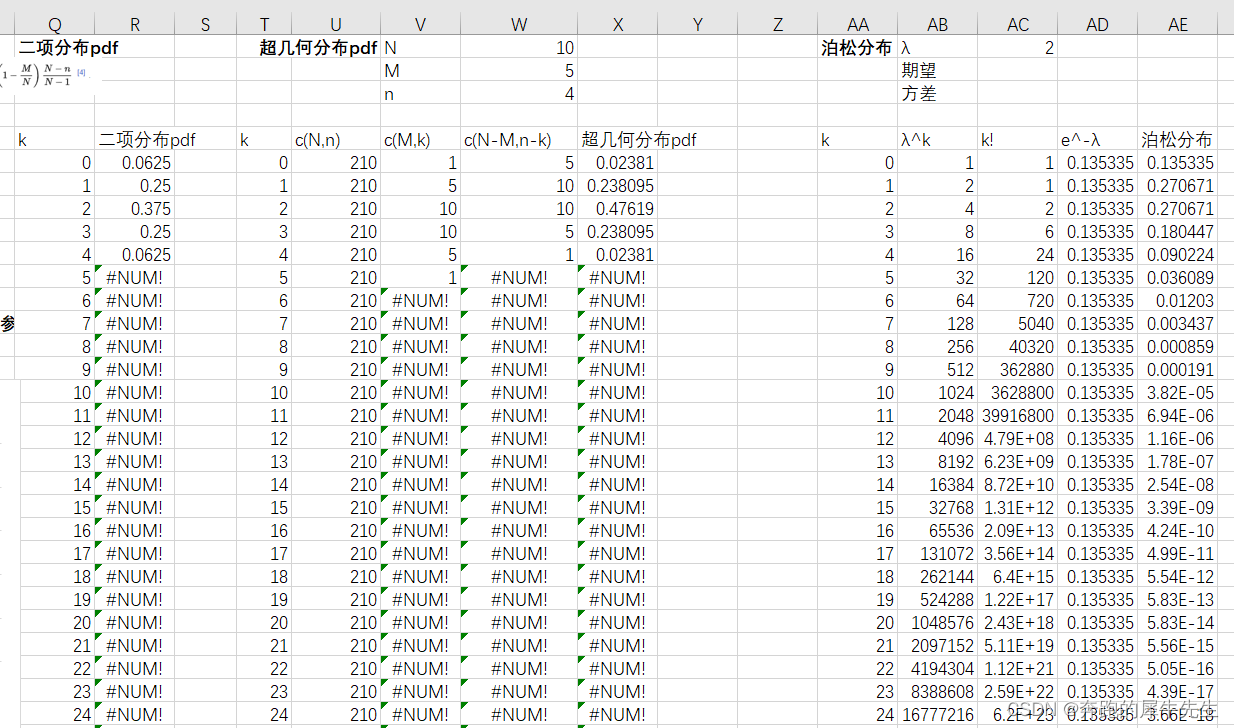
1 M,N都趋向∞时,超几何分布趋向二项分布
2 n足够大,np固定,二项分布概率收敛于泊松分布,
近似成立的前提要求n足够大,而p足够小,np不是很小
3 他们的期望都是一样的,概率分布pdf不同
4 其中超几何分布3个参数,二项分布2个参数,泊松分布1个参数
M/N 趋向于P,而np=λ
画图注意
为了看出明显差别,只取前5个数据做曲线比较即可
比较整体的动态过程,增加实验次数时
- 把数据总量S扩展到30条,
- 手动修改实验次数可以发现动态规律
- 那就是二项分布的PDF图形在趋向于 泊松分布
比较整体的动态过程,增加实验次数时
把数据总量S扩展到30条,
手动修改实验次数可以发现动态规律
那就是二项分布的PDF图形在趋向于 泊松分布