【数据结构】二叉树详解(1)-编程知识

【数据结构】二叉树详解(1)

⭐️ 前言

✨ 二叉树的概念性质

⭐️ 二叉树链式结构的实现

结构定义：

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>typedef int BinaryTreeDataType;typedef struct BinaryTreeNode {BinaryTreeDataType value;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BinaryTreeNode;

⭕️ 二叉树的遍历

按照规则，二叉树的遍历分为：前序/中序/后序的递归遍历。

前序遍历(PreOrder Traversal)：访问根节点的操作发生在遍历其左右子树之前。
- 根 -> 左子树 -> 右子树
中序遍历(InOrder Traversal)：访问根节点的操作发生在遍历左右子树之间。
- 左子树 -> 根 -> 右子树
后序遍历(PostOrder Traversal)：访问根节点的操作发生在遍历其左右子树之后。
- 左子树 -> 右子树 -> 根

在这里插入图片描述

PreOrder 代码：

// 前序遍历递归 根 -> 左子树 -> 右子树
void PreOrder(BinaryTreeNode* root) {if (root == NULL) {printf("# ");return;}printf("%d ", root->value);PreOrder(root->left);PreOrder(root->right);
}

前序递归流程图：
在这里插入图片描述

前序递归遍历顺序为：1 2 3 # # # 4 5 # # 6 # #

InOrder 代码：

// 中序遍历递归 左子树 -> 根 -> 右子树
void InOrder(BinaryTreeNode* root) {if (root == NULL) {printf("# ");return;}InOrder(root->left);printf("%d " , root->value);InOrder(root->right);
}

中序递归流程图：

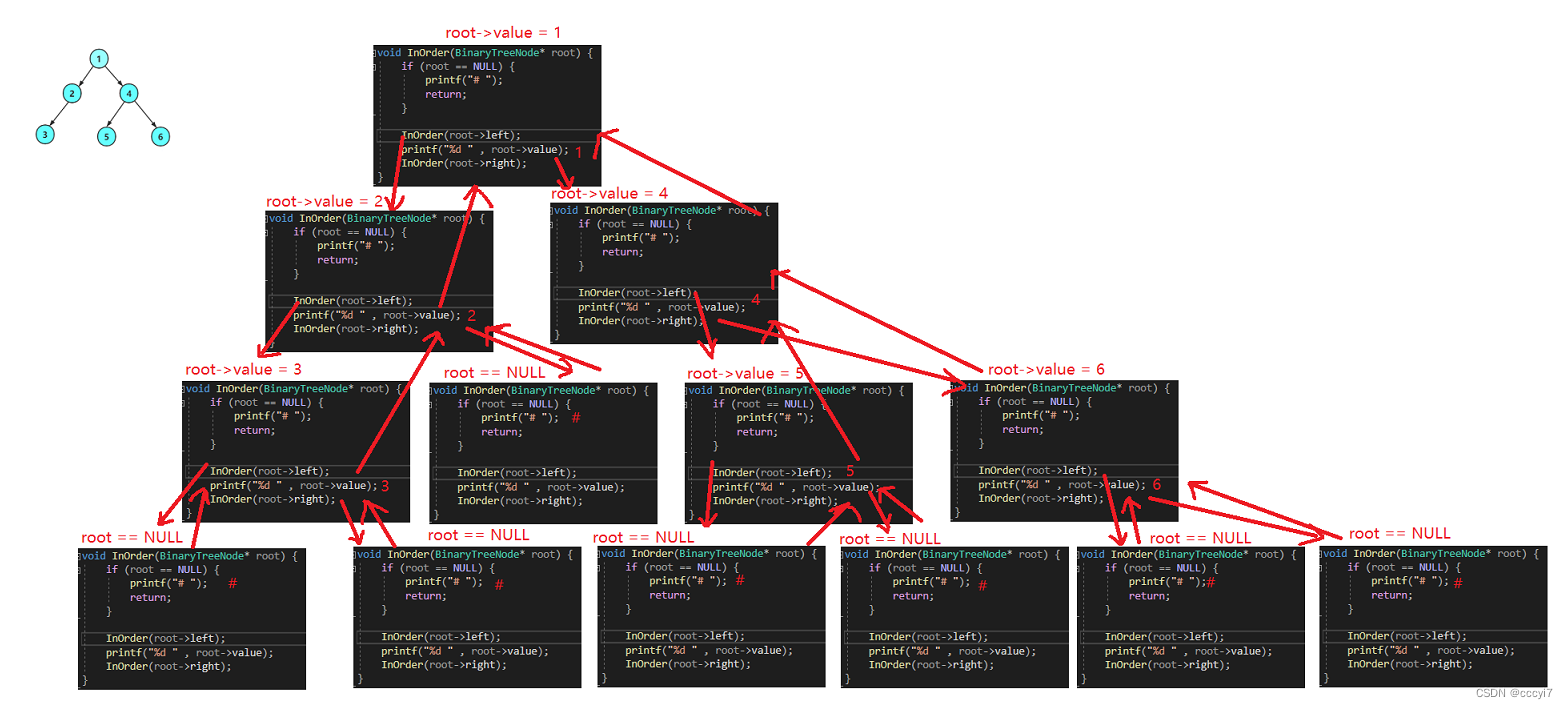
在这里插入图片描述

中序递归遍历顺序为：# 3 # 2 # 1 # 5 # 4 # 6 #

PostOrder 代码：

// 后序遍历递归 左子树 -> 右子树 -> 根
void PostOrder(BinaryTreeNode* root) {if (root == NULL) {printf("# ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d " , root->value);
}

后序递归流程图：
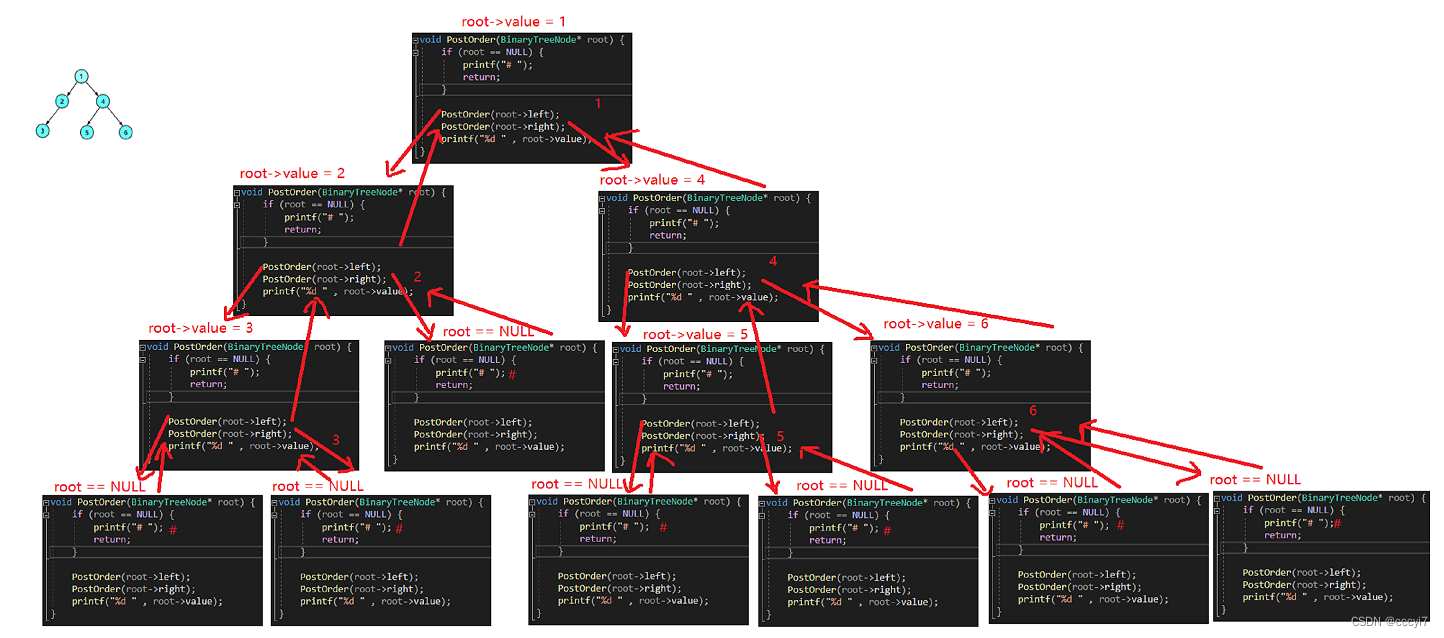
在这里插入图片描述
后序递归遍历顺序为：# # 3 # 2 # # 5 # # 6 4 1

注：# 代表空树

⭕️ 二叉树的其他接口

// 节点的数量
int BinaryTreeSize(BinaryTreeNode* root);
// 叶子节点的数量
int BinaryTreeLeafSize(BinaryTreeNode* root);
// 求k层节点的个数
int BinaryTreeKLevelSize(BinaryTreeNode* root , int k);
// 二叉树中查找某个元素
BinaryTreeNode* BinaryTreeFind(BinaryTreeNode* root , BinaryTreeDataType x);

BinaryTreeSize 代码：

// 节点的数量
int BinaryTreeSize(BinaryTreeNode* root) {if (root == NULL) {return 0;}return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}

BinaryTreeSize 递归流程图：
在这里插入图片描述

BinaryTreeLeafSize 代码：

// 叶子节点的数量
int BinaryTreeLeafSize(BinaryTreeNode* root) {if (root == NULL) {return 0;}if (root->left == NULL && root->right == NULL) {return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

BinaryTreeLeafSize 递归流程图：
在这里插入图片描述

BinaryTreeKLevelSize 代码：

// 求k层节点的个数
int BinaryTreeKLevelSize(BinaryTreeNode* root , int k) {assert(k >= 1);if (root == NULL) {return 0;}if (k == 1) {return 1;}return BinaryTreeKLevelSize(root->left , k - 1) + BinaryTreeKLevelSize(root->right , k - 1);
}

BinaryTreeKLevelSize 递归流程图：
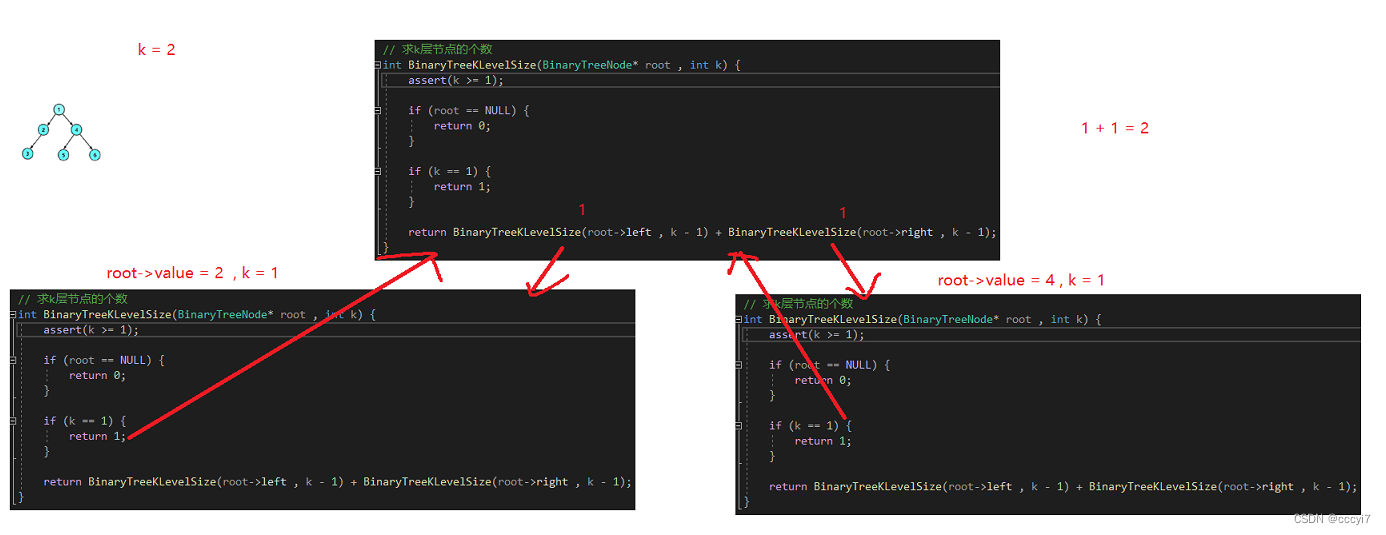
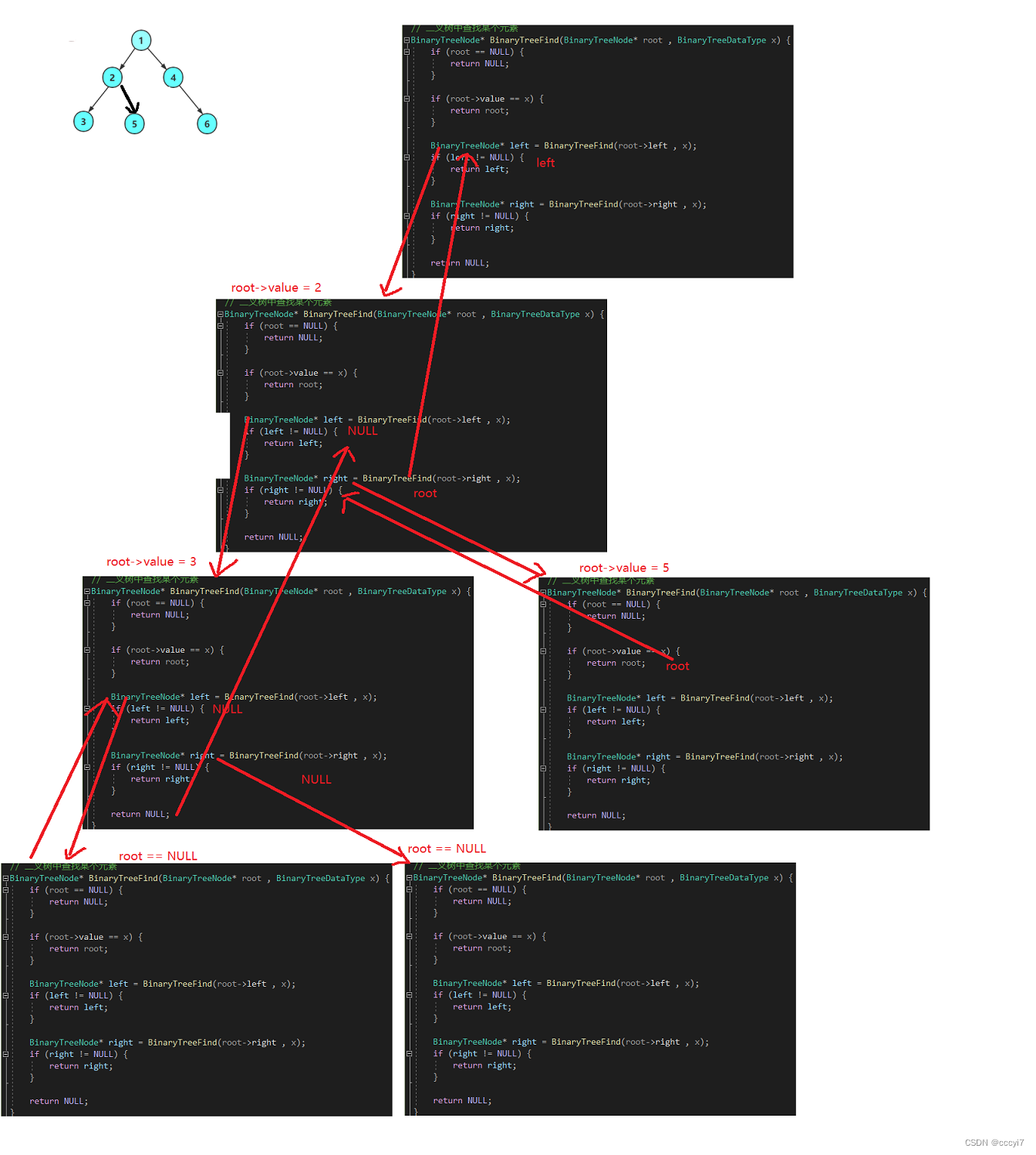
在这里插入图片描述

BinaryTreeFind 代码：

// 二叉树中查找某个元素
BinaryTreeNode* BinaryTreeFind(BinaryTreeNode* root , BinaryTreeDataType x) {if (root == NULL) {return NULL;}if (root->value == x) {return root;}BinaryTreeNode* left = BinaryTreeFind(root->left , x);if (left != NULL) {return left;}BinaryTreeNode* right = BinaryTreeFind(root->right , x);if (right != NULL) {return right;}return NULL;
}