3.3、Elastic-Net算法使用

这是scikit-learn官网给出的弹性网络回归的，损失函数公式，注意，它用的矩阵表示，里面用到范数运算。

$\underset{w}{\min }\frac{1}{2n_{\text{samples}}}||Xw-y|{|}_2^2+\alpha \rho ||w|{|}_1+\frac{\alpha (1-\rho )}{2}||w|{|}_2^2$

  Elastic-Net 回归，即岭回归和Lasso技术的混合。弹性网络是一种使用 L1， L2 范数作为先验正则项训练的线性回归模型。 这种组合允许学习到一个只有少量参数是非零稀疏的模型，就像 Lasso 一样，但是它仍然保持一些像 Ridge 的正则性质。我们可利用 l1_ratio 参数控制 L1 和 L2 的凸组合。

  弹性网络在很多特征互相联系（相关性，比如身高和体重就很有关系）的情况下是非常有用的。Lasso 很可能只随机考虑这些特征中的一个，而弹性网络更倾向于选择两个。

  在实践中，Lasso 和 Ridge 之间权衡的一个优势是它允许在迭代过程中继承 Ridge 的稳定性。

弹性网络回归和普通线性回归系数对比：

import numpy as np
from sklearn.linear_model import ElasticNet
from sklearn.linear_model import SGDRegressor, LinearRegression

创建数据并获取到原方程的系数

# 1、创建数据集X,y
X = 2 * np.random.rand(100, 20)
w = np.random.randn(20, 1)
b = np.random.randint(1, 10, size=1)
y = X.dot(w) + b + np.random.randn(100,1)print('原始方程的斜率：',w.ravel())
print('原始方程的截距：',b)

线性回归的系数

linear = LinearRegression()
linear.fit(X, y)
print('普通线性回归系数:',linear.coef_,linear.intercept_)

弹性网络算法

# 获取弹性网络
model = ElasticNet(alpha=1.11,l1_ratio=0.1)
model.fit(X, y)
print("弹性网络系数",model.coef_,model.intercept_)

随机梯度下降

# 随机梯度下降  ,可以变化为ridge Lasso  elastic
sgd = SGDRegressor(penalty='elasticnet',alpha=0.1)
sgd.fit(X, y.ravel())
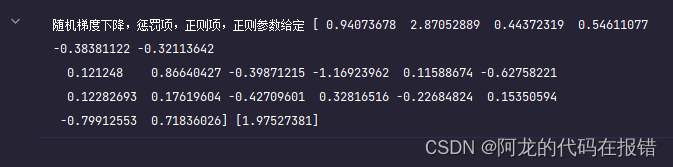
print('随机梯度下降，惩罚项，正则项，正则参数给定',sgd.coef_,sgd.intercept_)