代码随想录算法训练营第二十天 |654.最大二叉树、 617.合并二叉树、700.二叉搜索树中的搜索、 98.验证二叉搜索树-编程知识

今天学习内容：654.最大二叉树、 617.合并二叉树、700.二叉搜索树中的搜索、 98.验证二叉搜索树

讲解：代码随想录

654.最大二叉树

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

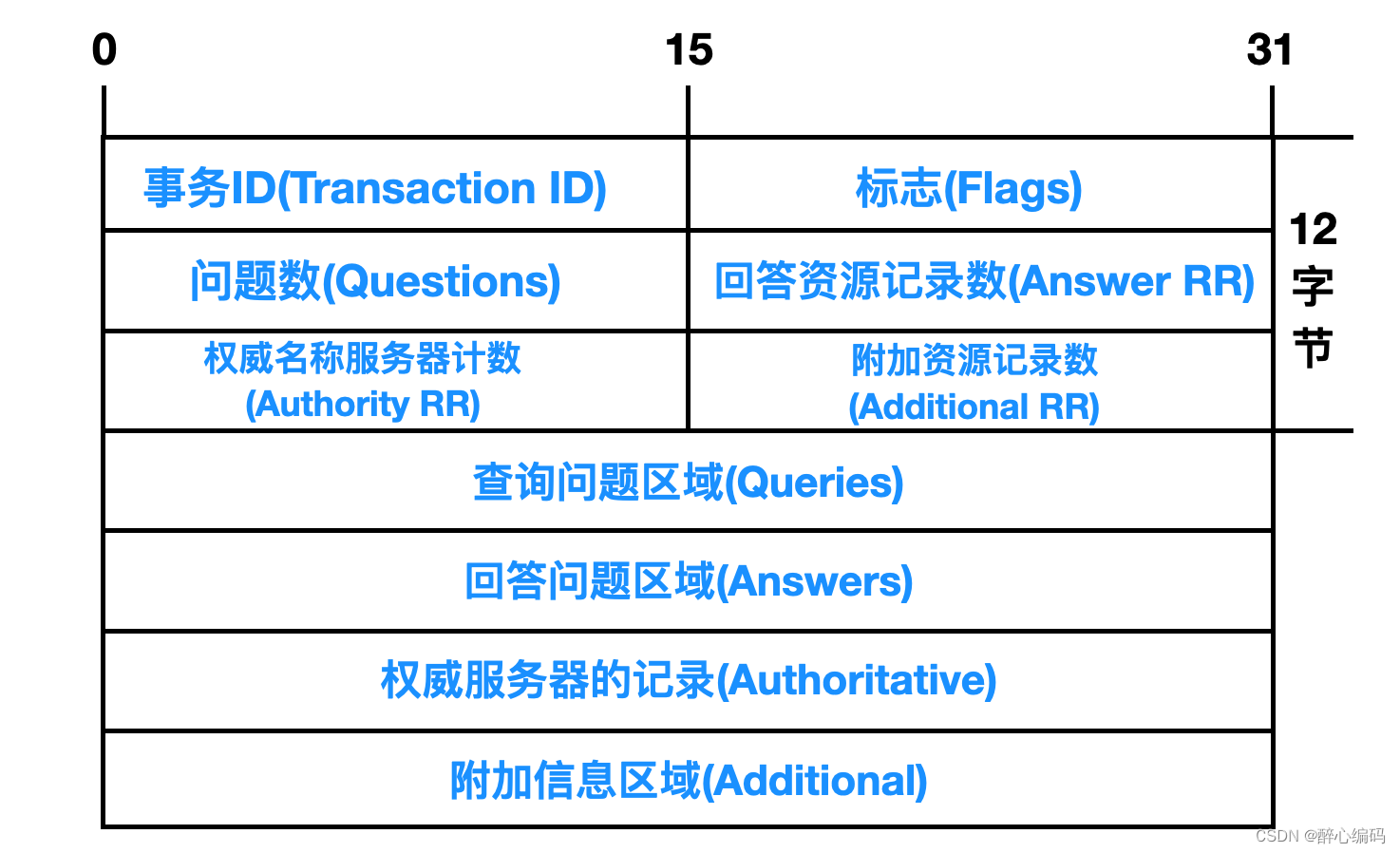
最大二叉树的构建过程如上，图片来源于代码随想录。

构造树一般采用的是前序遍历，因为先构造中间节点，然后递归构造左子树和右子树。

1.确定递归函数的参数和返回值

参数传入的是存放元素的数组，返回该数组构造的二叉树的头结点，返回类型是指向节点的指针。

TreeNode* constructMaximumBinaryTree(vector<int>& nums)

2.确定终止条件

题目中说了输入的数组大小一定是大于等于1的，所以我们不用考虑小于1的情况，那么当递归遍历的时候，如果传入的数组大小为1，说明遍历到了叶子节点了。

那么应该定义一个新的节点，并把这个数组的数值赋给新的节点，然后返回这个节点。这表示一个数组大小是1的时候，构造了一个新的节点，并返回。

TreeNode* node = new TreeNode(0);
if (nums.size() == 1) {node->val = nums[0];return node;
}

3.确定单层递归的逻辑

这里有三步工作

3.1先要找到数组中最大的值和对应的下标，最大的值构造根节点，下标用来下一步分割数组。

int maxValue = 0;
int maxValueIndex = 0;
for (int i = 0; i < nums.size(); i++) {if (nums[i] > maxValue) {maxValue = nums[i];maxValueIndex = i;}
}
TreeNode* node = new TreeNode(0);
node->val = maxValue;

3.2最大值所在的下标左区间构造左子树

这里要判断maxValueIndex > 0，因为要保证左区间至少有一个数值。

if (maxValueIndex > 0) {vector<int> newVec(nums.begin(), nums.begin() + maxValueIndex);node->left = constructMaximumBinaryTree(newVec);
}

3.3最大值所在的下标右区间构造右子树

判断maxValueIndex < (nums.size() - 1)，确保右区间至少有一个数值。

if (maxValueIndex < (nums.size() - 1)) {vector<int> newVec(nums.begin() + maxValueIndex + 1, nums.end());node->right = constructMaximumBinaryTree(newVec);
}

这样我们就分析完了，整体代码如下：

class Solution {
public:TreeNode* constructMaximumBinaryTree(vector<int>& nums) {TreeNode* node = new TreeNode(0);if (nums.size() == 1) {node->val = nums[0];return node;}// 找到数组中最大的值和对应的下标int maxValue = 0;int maxValueIndex = 0;for (int i = 0; i < nums.size(); i++) {if (nums[i] > maxValue) {maxValue = nums[i];maxValueIndex = i;}}node->val = maxValue;// 最大值所在的下标左区间 构造左子树if (maxValueIndex > 0) {vector<int> newVec(nums.begin(), nums.begin() + maxValueIndex);node->left = constructMaximumBinaryTree(newVec);}// 最大值所在的下标右区间 构造右子树if (maxValueIndex < (nums.size() - 1)) {vector<int> newVec(nums.begin() + maxValueIndex + 1, nums.end());node->right = constructMaximumBinaryTree(newVec);}return node;}
};

617.合并二叉树

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

递归三部曲来解决：

1.确定递归函数的参数和返回值：

首先要合入两个二叉树，那么参数至少是要传入两个二叉树的根节点，返回值就是合并之后二叉树的根节点。

TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {

2.确定终止条件：

因为是传入了两个树，那么就有两个树遍历的节点t1 和 t2，如果t1 == NULL 了，两个树合并就应该是 t2 了（如果t2也为NULL也无所谓，合并之后就是NULL）。

反过来如果t2 == NULL，那么两个数合并就是t1（如果t1也为NULL也无所谓，合并之后就是NULL）。

if (t1 == NULL) return t2; // 如果t1为空，合并之后就应该是t2
if (t2 == NULL) return t1; // 如果t2为空，合并之后就应该是t1

3.确定单层递归的逻辑：

单层递归的逻辑就比较好写了，这里我们重复利用一下t1这个树，t1就是合并之后树的根节点（就是修改了原来树的结构）。

那么单层递归中，就要把两棵树的元素加到一起。

t1->val += t2->val;

接下来t1 的左子树是：合并 t1左子树 t2左子树之后的左子树。

t1 的右子树：是合并 t1右子树 t2右子树之后的右子树。

最终t1就是合并之后的根节点。

t1->left = mergeTrees(t1->left, t2->left);
t1->right = mergeTrees(t1->right, t2->right);
return t1;

此时前序遍历，完整代码就写出来了，如下：

class Solution {
public:TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {if (t1 == NULL) return t2; // 如果t1为空，合并之后就应该是t2if (t2 == NULL) return t1; // 如果t2为空，合并之后就应该是t1// 修改了t1的数值和结构t1->val += t2->val;                             // 中t1->left = mergeTrees(t1->left, t2->left);      // 左t1->right = mergeTrees(t1->right, t2->right);   // 右return t1;}
};

700.二叉搜索树中的搜索

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

二叉搜索树是一个有序树：

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
它的左、右子树也分别为二叉搜索树

递归法

1.确定递归函数的参数和返回值

递归函数的参数传入的就是根节点和要搜索的数值，返回的就是以这个搜索数值所在的节点。

TreeNode* searchBST(TreeNode* root, int val)

2.确定终止条件

如果root为空，或者找到这个数值了，就返回root节点。

if (root == NULL || root->val == val) return root;

3.确定单层递归的逻辑

看看二叉搜索树的单层递归逻辑有何不同。

因为二叉搜索树的节点是有序的，所以可以有方向的去搜索。

如果root->val > val，搜索左子树，如果root->val < val，就搜索右子树，最后如果都没有搜索到，就返回NULL。

TreeNode* result = NULL;
if (root->val > val) result = searchBST(root->left, val);
if (root->val < val) result = searchBST(root->right, val);
return result;

整体代码如下：

class Solution {
public:TreeNode* searchBST(TreeNode* root, int val) {if (root == NULL || root->val == val) return root;TreeNode* result = NULL;if (root->val > val) result = searchBST(root->left, val);if (root->val < val) result = searchBST(root->right, val);return result;}
};

98.验证二叉搜索树

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

递归法

可以递归中序遍历将二叉搜索树转变成一个数组，代码如下：

vector<int> vec;
void traversal(TreeNode* root) {if (root == NULL) return;traversal(root->left);vec.push_back(root->val); // 将二叉搜索树转换为有序数组traversal(root->right);
}

比较一下，这个数组是否是有序的，注意二叉搜索树中不能有重复元素。

traversal(root);
for (int i = 1; i < vec.size(); i++) {// 注意要小于等于，搜索树里不能有相同元素if (vec[i] <= vec[i - 1]) return false;
}
return true;

整体代码如下：

class Solution {
private:vector<int> vec;void traversal(TreeNode* root) {if (root == NULL) return;traversal(root->left);vec.push_back(root->val); // 将二叉搜索树转换为有序数组traversal(root->right);}
public:bool isValidBST(TreeNode* root) {vec.clear(); // 不加这句在leetcode上也可以过，但最好加上traversal(root);for (int i = 1; i < vec.size(); i++) {// 注意要小于等于，搜索树里不能有相同元素if (vec[i] <= vec[i - 1]) return false;}return true;}
};