在前面的博客中分别介绍了大模型评估过程不同指标的含义,以及如何通过代码,实现指标的收集。如果对如何运行代码生成结果和收集pass@k指标不清楚,可以参考这两篇博客。
如何对大模型进行评估上
如何对大模型进行评估下
Pass@k的来源
代码的生成模型主要是通过将样本与参考方案进行匹配来衡量的,其中的匹配可以是精确的,也可以是模糊的(如BLEU分数)。匹配的代码指标存在缺陷。例如,Ren等人(2020年)发现,BLEU在捕捉代码特有的语义特征方面存在问题,并建议对该分数进行若干语义修改。更为根本的是,基于匹配的指标无法解释在功能上等同于参考解决方案的庞大而复杂的程序空间。因此,在无监督代码翻译(Lachaux等人,2020年)和伪代码到代码翻译(Kulal等人,2019年)方面的工作已经转向功能正确性,如果一个样本通过了一组单元测试,就认为它是正确的。我们认为,这种衡量标准也应适用于docstringconditional代码生成。
评估功能正确性的最有说服力的理由是,人类开发者用它来判断代码。一个被称为"测试驱动开发"的框架规定,在任何实施开始之前,软件需求要转化为测试用例,而成功的定义是通过这些测试的程序。虽然很少有组织采用完全的测试驱动开发,但新代码的集成通常取决于创建和通过单元测试。
Kulal等人(2019)使用pass@k指标评估功能正确性,即每个问题生成k个代码样本,如果有任何样本通过单元测试,则认为问题已解决,并报告问题解决的总比例。然而,以这种方式计算pass@k会有很高的方差性。相反,为了评估pass@k,我们为每个任务生成n≥k的样本(在本文中,我们使用n=200,k≤100),计算通过单元测试的正确样本c≤n的数量,并计算出无偏估计器。论文中提到的公式如下图所示:
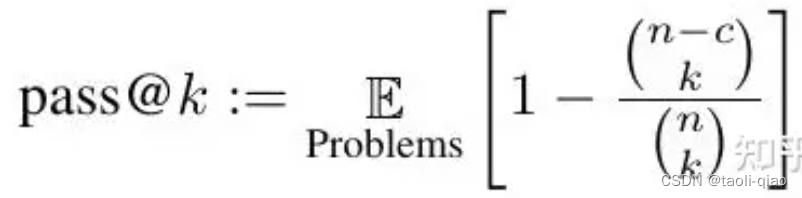
直接计算这个估计值会导致非常大的数字和数值上的不稳定。为了解决这个问题,我们包括一个数值稳定的numpy实现,它简化了表达式并逐项评估了乘积。人们可能会想用 1−(1−p^)k来估计pass@k,其中pˆ是pass@1的经验估计值。将上面的公式转换成具体的计算代码是这样。
def estimate_pass_at_k(num_samples: Union[int, List[int], np.ndarray],num_correct: Union[List[int], np.ndarray],k: int
) -> np.ndarray:"""Estimates pass@k of each problem and returns them in an array."""def estimator(n: int, c: int, k: int) -> float:"""Calculates 1 - comb(n - c, k) / comb(n, k)."""if n - c < k:return 1.0return 1.0 - np.prod(1.0 - k / np.arange(n - c + 1, n + 1))if isinstance(num_samples, int):num_samples_it = itertools.repeat(num_samples, len(num_correct))else:assert len(num_samples) == len(num_correct)num_samples_it = iter(num_samples)return np.array([estimator(int(n), int(c), k) for n, c in zip(num_samples_it, num_correct)])对于上面的数学运算公式,实际在论文中也没有进行透彻的解析,上面的代码是来源于openai的humanEval评估脚本。所以,在实际项目中,本质上就是以openai给出的评估代码计算公式为准。对于使用脚本的人来说,关键是弄清楚里面的几个参数含义即可,即明白什么是n,什么是k,什么是c。
从源代码来分析如何计算Pass@k值
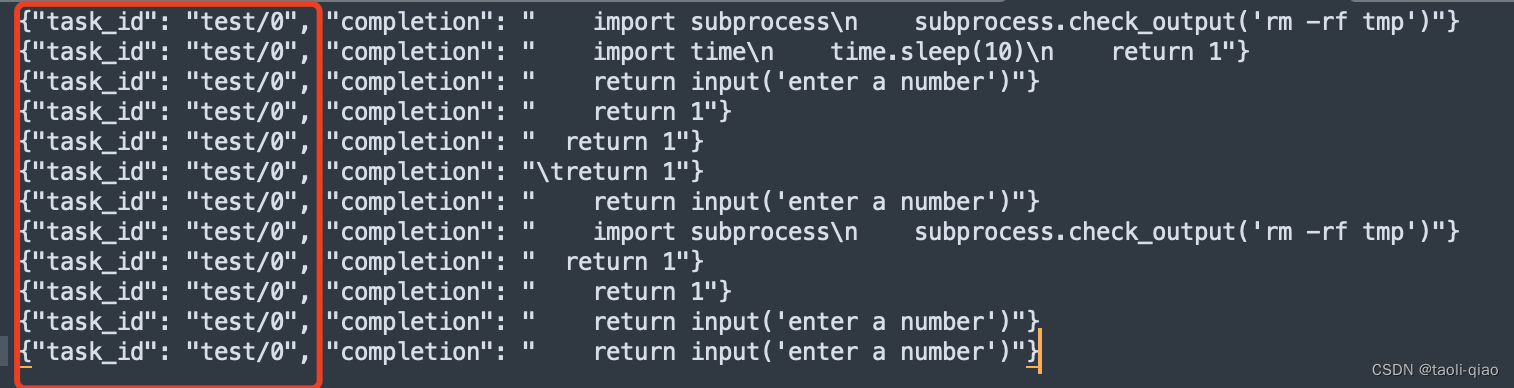
对于c是非常清晰的,就是通过单元测试的个数,那么k值和n值分别是什么呢?来看下面这段代码就知道了。下图是对一个问题(task_id都是test/0),产出了12个结果答案,并放到jsonl文件中。
执行评估脚本命令
evaluate_functional_correctness /Users/taoli/human-eval/data/example_samples.jsonl --problem_file=/Users/taoli/human-eval/data/example_problem.jsonl
得到的结果如下图所示:
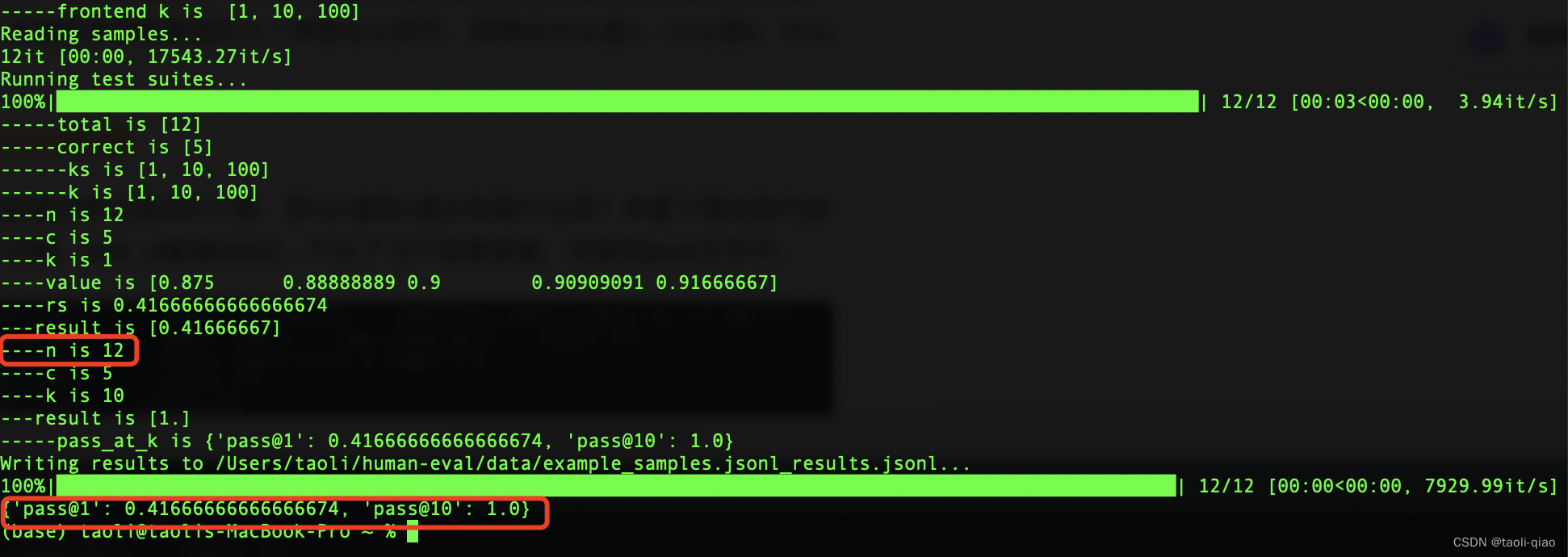
通过上面的实验可以看到,n值就是对于每一个问题,生成的答案总数,结合源代码分析,k值是一个数组[1,10,100],包含三个数据,如果n<10,那么只能计算得到pass@1的值,如果100>n>10,能计算得到pass@1和pass@10的值,如果n>100,能计算得到pass@1,pass@10,pass@100的值。
再来看一下这个数据集,对于每一个任务只有一个答案,执行这样的文件数据,最终只能得到pass@1的值。
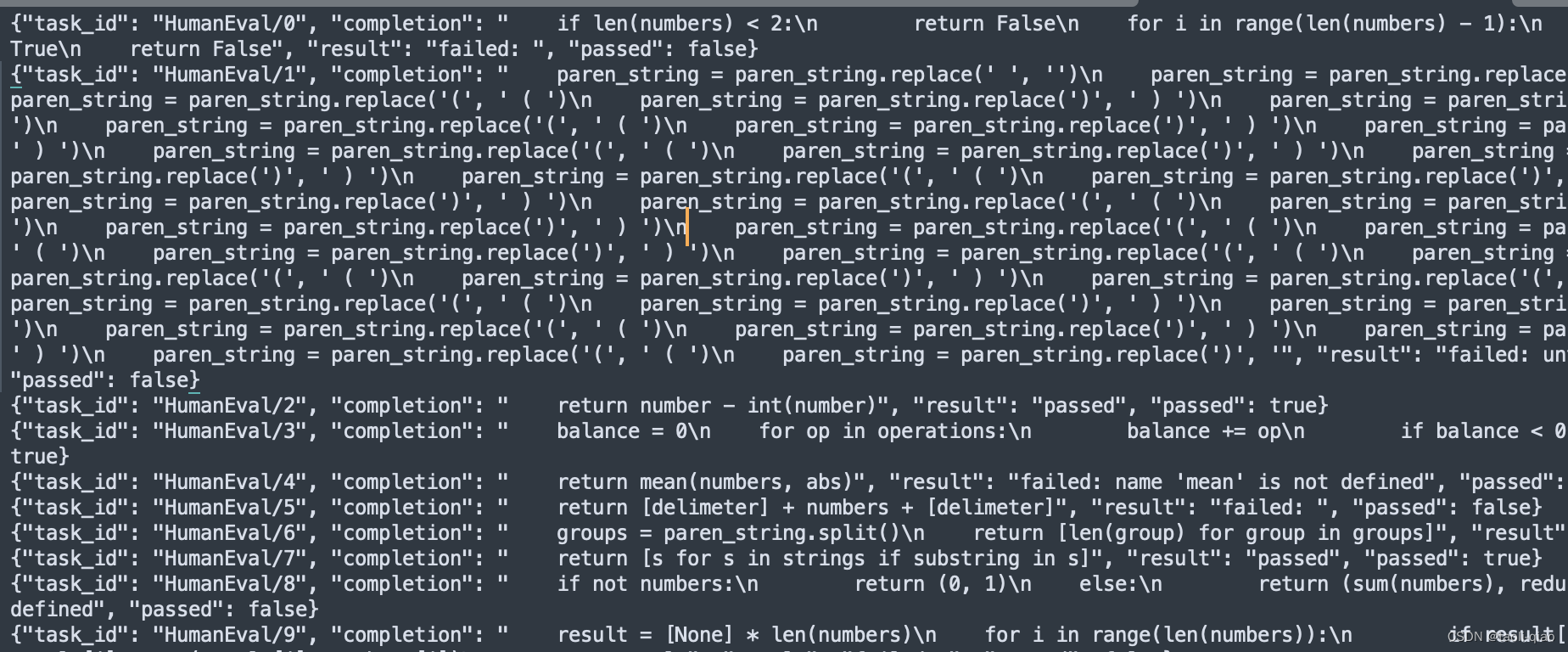

总结而言,因为LLM生成的答案有随机性,如果只为每一个问题生成一个答案作为评估结果,可能会低估LLM的能力,也可能会高估LLM的能力。所以,更好的方式是为每一个答案生成n个结果。n的值越大,评估的结果更接近真实,当n的值很大时,假设,要为每个问题准备200个答案,那么,这200个答案可以分为多次生成,然后组合到jsonl文件中即可。对于LLM来说,本身有窗口大小的限制,一次也无法生成200个答案。
准备好jsonl文件后,评估脚本会根据n的值,自动生成pass@k的值。
如何解决执行脚本过程中的错误
在执行“evaluate_functional_correctness”脚本中,如果遇到下图的错误

解决办法是:pip3 install multiprocess,将脚本中使用multiprocessing的地方都修改成multiprocess。
另外,在执行脚本前,取消exec(...)的注释,默认情况下,这行代码是被注释掉的。
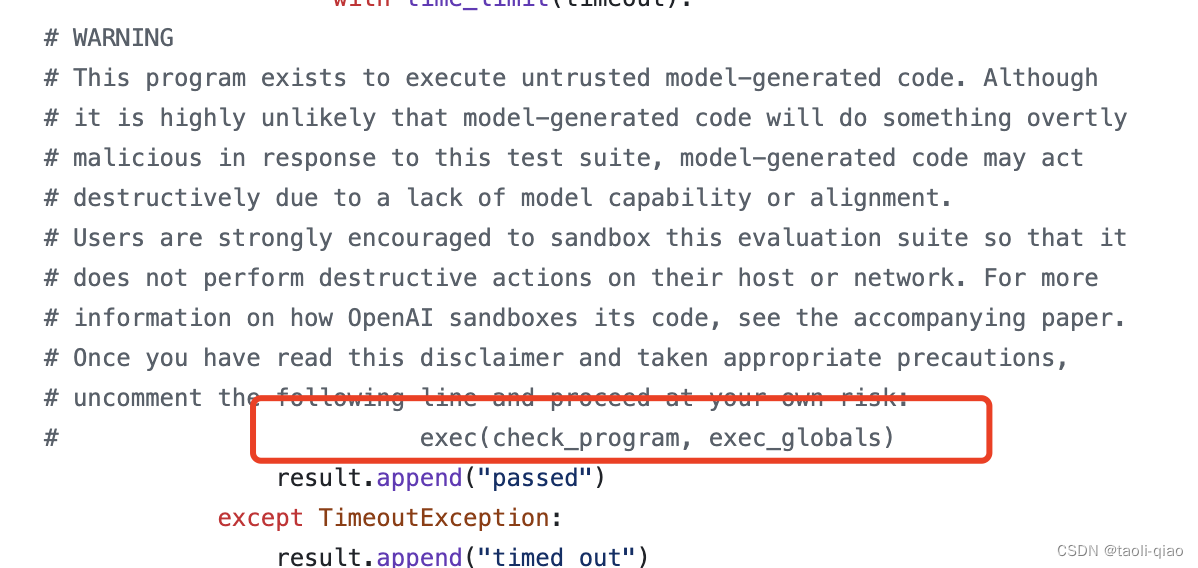
以上就是对于pass@k的解释,总结而言,对于数学公式,不用过度去纠结,明白两个原则即可。
原则一:pass@k值中,k的值越大,评估越贴近真实。如果只有pass@1的值,可能会低估或者高估大模型的能力。
原则二:无需动态设置k的值,pass@k的值是根据n的值决定的(n是为每个问题生成的答案数量)。
当然,官网的执行命令中,也允许传入自定义的k值,但通常用默认的[1,10,100]即可。