JAVA代码编写

84. 柱状图中最大的矩形

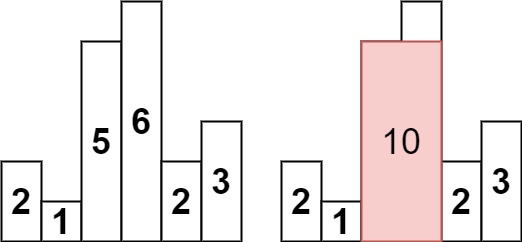
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

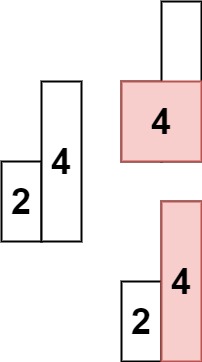
输入： heights = [2,4]
输出： 4

方法一：暴力解法

思路：两个for循环，第一个循环i控制heights的起始位置，第二个循环i控制heights的结束位置，每次记录i-j的矩形面积，去最大的直到遍历结束。

力扣上没法通过

复杂度分析：

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(1)$

public class Solution {public static int getMaxRectangleArea(int[] heights) {int maxArea = 0;int length = heights.length;for (int i = 0; i < length; i++) {int minHeight = Integer.MAX_VALUE;for (int j = i; j < length; j++) {minHeight = Math.min(minHeight, heights[j]);int width = j - i + 1;int area = minHeight * width;maxArea = Math.max(maxArea, area);}}return maxArea;}public static void main(String[] args) {int[] heights = {2, 1, 5, 6, 2, 3};int maxArea = getMaxRectangleArea(heights);System.out.println("最大矩形面积：" + maxArea);}
}

方法二：左右指针

思路：遍历下标i，找到左边小于等于当前高度，找到右边小于等于当前高度，这样宽度就是右指针-左指针+1，高度就是hegihts[i]，从而计算面积，每次记录最大的面积。

复杂度分析：

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(1)$

class Solution {public int largestRectangleArea(int[] heights) {int maxArea = 0;int length = heights.length;for (int i = 0; i < length; i++) {int left = i;int right = i;// 找到左边第一个小于 heights[i] 的位置while (left > 0 && heights[left - 1] >= heights[i]) {left--;}// 找到右边第一个小于 heights[i] 的位置while (right < length - 1 && heights[right + 1] >= heights[i]) {right++;}int width = right - left + 1;int area = heights[i] * width;maxArea = Math.max(maxArea, area);}return maxArea;}
}

方法三：单调栈

思路：

复杂度分析：

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

import java.util.Stack;class Solution {public int largestRectangleArea(int[] heights) {int[] newHeight = new int[heights.length + 2];System.arraycopy(heights, 0, newHeight, 1, heights.length); // 将原数组heights从下标0 开始复制到 新数组newHeight的下标1位置newHeight[heights.length+1] = 0;Stack<Integer> stack = new Stack<>();stack.push(0);int res = 0;for (int i = 1; i < newHeight.length; i++) {while (newHeight[i] < newHeight[stack.peek()]) {int mid = stack.pop();int w = i - stack.peek() - 1;int h = newHeight[mid];res = Math.max(res, w * h);}stack.push(i);}return res;}public static void main(String[] args) {Solution solution = new Solution();solution.largestRectangleArea(new int[]{2,1,5,6,2,3});}
}