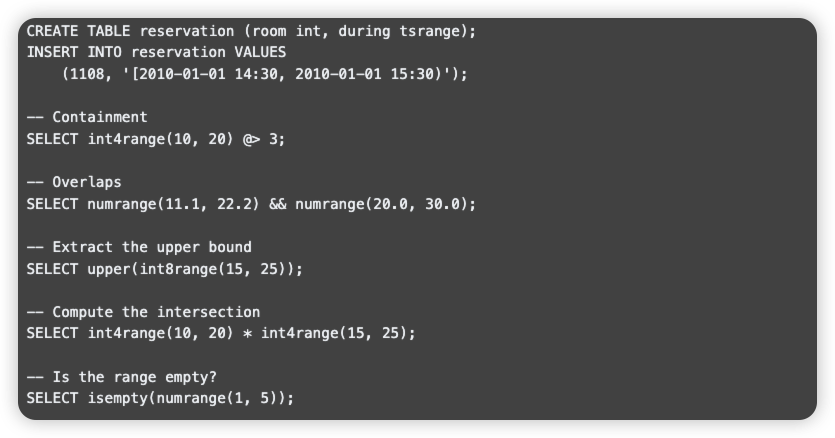
整数规划-割平面法
- 割平面法思想
- Gomory's割平面法原理
- 实例
谨以此博客作为学习期间的记录。
割平面法思想
在之前,梳理了分支定界法的流程:分支定界法
除了分支定界法,割平面法也是求解整数规划的另一个利器。
我们已经知道,线性规划的可行域是一个凸集,而最优点将会在凸集的某个顶点处取到。而如果凸集的顶点都是整数点,那这样的话只要使用单纯形法即可求得整数最优解。
就像下图的凸包所示,在实际情况中,线性规划的可行域往往交点都不在整数点处,如果能找到整数点的一个凸包,那整数规划问题即可转化为普通的线性规划问题。但是想找到这样的一个凸包是非常困难的,只能使用某种方法去不断的逼近这个凸包。
这就是割平面法的思想:不断地向原问题中添加约束去逼近这个整数凸包,从而使得解出来的解为整数解。

Gomory’s割平面法原理
在上面提到了,通过不断添加约束去逼近一个整数凸包,那么该如何去添加约束呢?也就是如何确定割平面这是本部分的重点。
确定割平面的算法有很多,暂时先以较为基础的Gomory’s 分数割平面算法介绍,后续如果用到更多其他割平面再进行补充。
先看一个标准整数规划问题
m i n c T x s . t . { A x = b x ≥ 0 x ∈ Z n \begin{align*} min \quad & \mathbf{c}^T \mathbf{x} \\ s.t. \quad & \begin{cases} \mathbf{Ax} =\mathbf{b} \\ \mathbf{x} \geq \mathbf{0}\\ \mathbf{x} \in \mathbb{Z}^n \end{cases} \\ \end{align*} mins.t.cTx⎩ ⎨ ⎧Ax=bx≥0x∈Zn
当使用单纯形法求解整数规划问题时,可以将问题划分为基变量(Basic Variables)和非基变量(Non-Basic Variables)。在标准形式的整数规划问题中,可以进行如下的续写:
令基变量为 x B \mathbf{x}_B xB,非基变量为 x N \mathbf{x}_N xN。整数规划问题可以表示为:
min c T x = c B T x B + c N T x N \min \mathbf{c}^T \mathbf{x} = \mathbf{c}_B^T \mathbf{x}_B + \mathbf{c}_N^T \mathbf{x}_N mincTx=cBTxB+cNTxN
约束条件:
B x B + N x N = b x B , x N ≥ 0 x ∈ Z n \begin{align*} \mathbf{B} \mathbf{x}_B + \mathbf{N} \mathbf{x}_N &= \mathbf{b} \\ \mathbf{x}_B, \mathbf{x}_N &\geq \mathbf{0} \\ \mathbf{x} &\in \mathbb{Z}^n \end{align*} BxB+NxNxB,xNx=b≥0∈Zn
其中:
- c T = [ c B T , c N T ] \mathbf{c}^T = [\mathbf{c}_B^T, \mathbf{c}_N^T] cT=[cBT,cNT] 是目标函数的系数向量, c B \mathbf{c}_B cB 对应基变量的系数, c N \mathbf{c}_N cN 对应非基变量的系数。
- B \mathbf{B} B 和 N \mathbf{N} N 分别是基变量和非基变量对应的约束矩阵的子矩阵。
- x B \mathbf{x}_B xB 和 x N \mathbf{x}_N xN 分别是基变量和非基变量向量。
现在将整数约束松弛掉,使用单纯形法进行求解,多次迭代后模型收敛。收敛后的问题可以表述如下:
min f 0 + c N T x N \min \quad f_0 + \mathbf{c}_N^T \mathbf{x}_N minf0+cNTxN
约束条件:
x B + B − 1 N x N = B − 1 b x B , x N ≥ 0 \begin{align*} \mathbf{x}_B + \mathbf{B}^{-1}\mathbf{N} \mathbf{x}_N &= \mathbf{B}^{-1}\mathbf{b} \\ \mathbf{x}_B, \mathbf{x}_N &\geq \mathbf{0} \\ \end{align*} xB+B−1NxNxB,xN=B−1b≥0
其中 f 0 = c B T x B f_0 = \mathbf{c}_B^T \mathbf{x}_B f0=cBTxB在求解之后为一个常数。
那么将上述约束变形即可得到 x B + ⌊ B − 1 N ⌋ x N ≤ ⌊ B − 1 b ⌋ \mathbf{x}_B + \lfloor\mathbf{B}^{-1}\mathbf{N} \rfloor \mathbf{x}_N \leq \lfloor \mathbf{B}^{-1}\mathbf{b} \rfloor xB+⌊B−1N⌋xN≤⌊B−1b⌋将其与原约束相减可以得到
( B − 1 N − ⌊ B − 1 N ⌋ ) x N ≥ B − 1 b − ⌊ B − 1 b ⌋ (\mathbf{B}^{-1}\mathbf{N} - \lfloor\mathbf{B}^{-1}\mathbf{N} \rfloor )\mathbf{x}_N \geq \mathbf{B}^{-1}\mathbf{b} - \lfloor \mathbf{B}^{-1}\mathbf{b} \rfloor (B−1N−⌊B−1N⌋)xN≥B−1b−⌊B−1b⌋
这个约束可以割掉小数解得部分,原因如下。
如果最终解出来的仍为小数解,表示为[ x B , x N x_B,x_N xB,xN],其中 x B x_B xB为小数解, x N = 0 x_N = 0 xN=0,那么就有 B − 1 b \mathbf{B}^{-1}\mathbf{b} B−1b也为小数,那么就有 B − 1 b − ⌊ B − 1 b ⌋ > 0 \mathbf{B}^{-1}\mathbf{b} - \lfloor \mathbf{B}^{-1}\mathbf{b} \rfloor > 0 B−1b−⌊B−1b⌋>0,而 x N = 0 x_N = 0 xN=0就导致不等式右边大于0,不等式左边等于0.不等式不成立。因此为了使不等式成立,就需要满足最终的解为不能有小数解。
实例
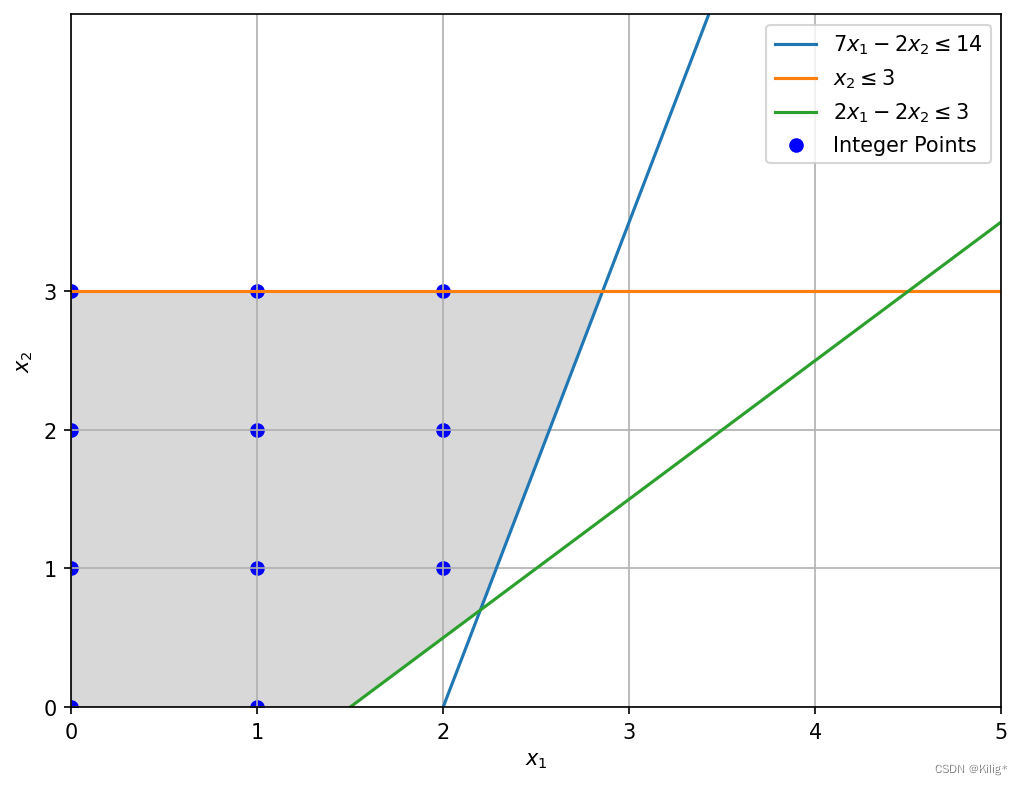
m a x z = 4 x 1 − x 2 s . t . { 7 x 1 − 2 x 2 ≤ 14 x 2 ≤ 3 2 x 1 − 2 x 2 ≤ 3 x 1 , x 2 ≥ 0 x ∈ Z n (整数限制) \begin{align*} max \quad &z = 4x_1 - x_2 \\ s.t. \quad & \begin{cases} 7x_1-2x_2 \leq 14 \\ x_2 \leq 3\\ 2x_1-2x_2 \leq 3\\ x_1,x_2 \geq 0\\ \mathbf{x} \in \mathbb{Z}^n \quad \text{(整数限制)} \end{cases} \\ \end{align*} maxs.t.z=4x1−x2⎩ ⎨ ⎧7x1−2x2≤14x2≤32x1−2x2≤3x1,x2≥0x∈Zn(整数限制)
可行域如下
求解松弛子问题1
m a x z = 4 x 1 − x 2 s . t . { 7 x 1 − 2 x 2 + x 3 = 14 x 2 + x 4 = 3 2 x 1 − 2 x 2 + x 5 = 3 x 1 , x 2 , x 3 , x 4 , x 5 ≥ 0 \begin{align*} max \quad &z = 4x_1 - x_2 \\ s.t. \quad & \begin{cases} 7x_1-2x_2+x_3 = 14 \\ x_2 + x_4 = 3\\ 2x_1-2x_2 +x_5 = 3\\ x_1,x_2,x_3,x_4,x_5 \geq 0\\ \end{cases} \\ \end{align*} maxs.t.z=4x1−x2⎩ ⎨ ⎧7x1−2x2+x3=14x2+x4=32x1−2x2+x5=3x1,x2,x3,x4,x5≥0
求解得到
Optimal objective value: 8.428571428571429
x1: 2.857142857142857
x2: 3.0
x3: 0.0
x4: 0.0
x5: 3.2857142857142865
以x1,x2,x5作为基变量,对约束进行等价变换(把约束中基变量的系数矩阵变为单位阵),变换之后的问题如下
m a x z = 4 x 1 − x 2 s . t . { 1 x 1 + 0 x 2 + 1 7 x 3 + 2 7 x 4 + 0 x 5 = 20 7 0 x 1 + 1 x 2 + 0 x 3 + 1 x 4 + 0 x 5 = 3 0 x 1 + 0 x 2 − 2 7 x 3 + 10 7 x 4 + 1 x 5 = 23 7 x 1 , x 2 , x 3 , x 4 , x 5 ≥ 0 \begin{align*} max \quad &z = 4x_1 - x_2 \\ s.t. \quad & \begin{cases} 1x_1+0x_2+\frac{1}{7}x_3+\frac{2}{7}x_4+0x_5 = \frac{20}{7} \\ 0x_1+1x_2 +0x_3+ 1x_4+0x_5 = 3\\ 0x_1+0x_2 -\frac{2}{7}x_3+\frac{10}{7}x_4+1x_5 = \frac{23}{7}\\ x_1,x_2,x_3,x_4,x_5 \geq 0\\ \end{cases} \\ \end{align*} maxs.t.z=4x1−x2⎩ ⎨ ⎧1x1+0x2+71x3+72x4+0x5=7200x1+1x2+0x3+1x4+0x5=30x1+0x2−72x3+710x4+1x5=723x1,x2,x3,x4,x5≥0
选择第一个约束,构造得到割平面不等式 1 7 x 3 + 2 7 x 4 ≥ 6 7 \frac{1}{7}x_3+\frac{2}{7}x_4\geq\frac{6}{7} 71x3+72x4≥76将这个约束化为标准形式 1 7 x 3 + 2 7 x 4 − s = 6 7 \frac{1}{7}x_3+\frac{2}{7}x_4-s = \frac{6}{7} 71x3+72x4−s=76加入到原问题中得到子问题2。
m a x z = 4 x 1 − x 2 s . t . { 1 x 1 + 0 x 2 + 1 7 x 3 + 2 7 x 4 + 0 x 5 = 20 7 0 x 1 + 1 x 2 + 0 x 3 + 1 x 4 + 0 x 5 = 3 0 x 1 + 0 x 2 − 2 7 x 3 + 10 7 x 4 + 1 x 5 = 23 7 1 7 x 3 + 2 7 x 4 − s = 6 7 x 1 , x 2 , x 3 , x 4 , x 5 , s ≥ 0 \begin{align*} max \quad &z = 4x_1 - x_2 \\ s.t. \quad & \begin{cases} 1x_1+0x_2+\frac{1}{7}x_3+\frac{2}{7}x_4+0x_5 = \frac{20}{7} \\ 0x_1+1x_2 +0x_3+ 1x_4+0x_5 = 3\\ 0x_1+0x_2 -\frac{2}{7}x_3+\frac{10}{7}x_4+1x_5 = \frac{23}{7}\\ \frac{1}{7}x_3+\frac{2}{7}x_4-s = \frac{6}{7}\\ x_1,x_2,x_3,x_4,x_5,s \geq 0\\ \end{cases} \\ \end{align*} maxs.t.z=4x1−x2⎩ ⎨ ⎧1x1+0x2+71x3+72x4+0x5=7200x1+1x2+0x3+1x4+0x5=30x1+0x2−72x3+710x4+1x5=72371x3+72x4−s=76x1,x2,x3,x4,x5,s≥0
求解得到
Optimal objective value: 7.500000000000002
x1: 2.0000000000000004
x2: 0.5000000000000004
x3: 1.0000000000000004
x4: 2.4999999999999996
x5: 0.0
s: 0.0
选择x1,x2,x3,x4作为基变量,继续对约束进行等价变换。
变换之后的问题如下:
m a x z = 4 x 1 − x 2 s . t . { 1 x 1 + 0 x 2 + 0 x 3 + 0 x 4 + 0 x 5 + 1 s = 2 0 x 1 + 1 x 2 + 0 x 3 + 0 x 4 − 1 2 x 5 + 1 s = 1 2 0 x 1 + 0 x 2 + 1 x 3 + 0 x 4 − 1 x 5 − 5 s = 1 0 x 1 + 0 x 2 + 0 x 3 + 1 x 4 + 1 2 x 5 − 1 s = 5 2 x 1 , x 2 , x 3 , x 4 , x 5 , s ≥ 0 \begin{align*} max \quad &z = 4x_1 - x_2 \\ s.t. \quad & \begin{cases} 1x_1+0x_2+0x_3+0x_4+0x_5+1s = 2 \\ 0x_1+1x_2 +0x_3+ 0x_4-\frac{1}{2}x_5+1s = \frac{1}{2}\\ 0x_1+0x_2+1x_3+0x_4-1x_5-5s = 1\\ 0x_1+0x_2+0x_3+1x_4+\frac{1}{2}x_5-1s = \frac{5}{2}\\ x_1,x_2,x_3,x_4,x_5,s \geq 0\\ \end{cases} \\ \end{align*} maxs.t.z=4x1−x2⎩ ⎨ ⎧1x1+0x2+0x3+0x4+0x5+1s=20x1+1x2+0x3+0x4−21x5+1s=210x1+0x2+1x3+0x4−1x5−5s=10x1+0x2+0x3+1x4+21x5−1s=25x1,x2,x3,x4,x5,s≥0
选择第二个继续构造不等式得到 1 2 x 5 ≥ 1 2 \frac{1}{2}x_5\geq\frac{1}{2} 21x5≥21标准化之后为 1 2 x 5 − s 1 = 1 2 \frac{1}{2}x_5-s_1 = \frac{1}{2} 21x5−s1=21加入到原问题中得到子问题3:
m a x z = 4 x 1 − x 2 s . t . { 1 x 1 + 0 x 2 + 0 x 3 + 0 x 4 + 0 x 5 + 1 s = 2 0 x 1 + 1 x 2 + 0 x 3 + 0 x 4 − 1 2 x 5 + 1 s = 1 2 0 x 1 + 0 x 2 + 1 x 3 + 0 x 4 − 1 x 5 − 5 s = 1 0 x 1 + 0 x 2 + 0 x 3 + 1 x 4 + 1 2 x 5 − 1 s = 5 2 1 2 x 5 − s 1 = 1 2 x 1 , x 2 , x 3 , x 4 , x 5 , s ≥ 0 \begin{align*} max \quad &z = 4x_1 - x_2 \\ s.t. \quad & \begin{cases} 1x_1+0x_2+0x_3+0x_4+0x_5+1s = 2 \\ 0x_1+1x_2 +0x_3+ 0x_4-\frac{1}{2}x_5+1s = \frac{1}{2}\\ 0x_1+0x_2+1x_3+0x_4-1x_5-5s = 1\\ 0x_1+0x_2+0x_3+1x_4+\frac{1}{2}x_5-1s = \frac{5}{2}\\ \frac{1}{2}x_5-s_1 = \frac{1}{2}\\ x_1,x_2,x_3,x_4,x_5,s \geq 0\\ \end{cases} \\ \end{align*} maxs.t.z=4x1−x2⎩ ⎨ ⎧1x1+0x2+0x3+0x4+0x5+1s=20x1+1x2+0x3+0x4−21x5+1s=210x1+0x2+1x3+0x4−1x5−5s=10x1+0x2+0x3+1x4+21x5−1s=2521x5−s1=21x1,x2,x3,x4,x5,s≥0
求解得到
Optimal objective value: 7.0
x1: 2.0
x2: 1.0
x3: 2.0
x4: 2.0
x5: 1.0
s: 0.0
s1: 0.0
得到了整数解。
博客中涉及到的代码