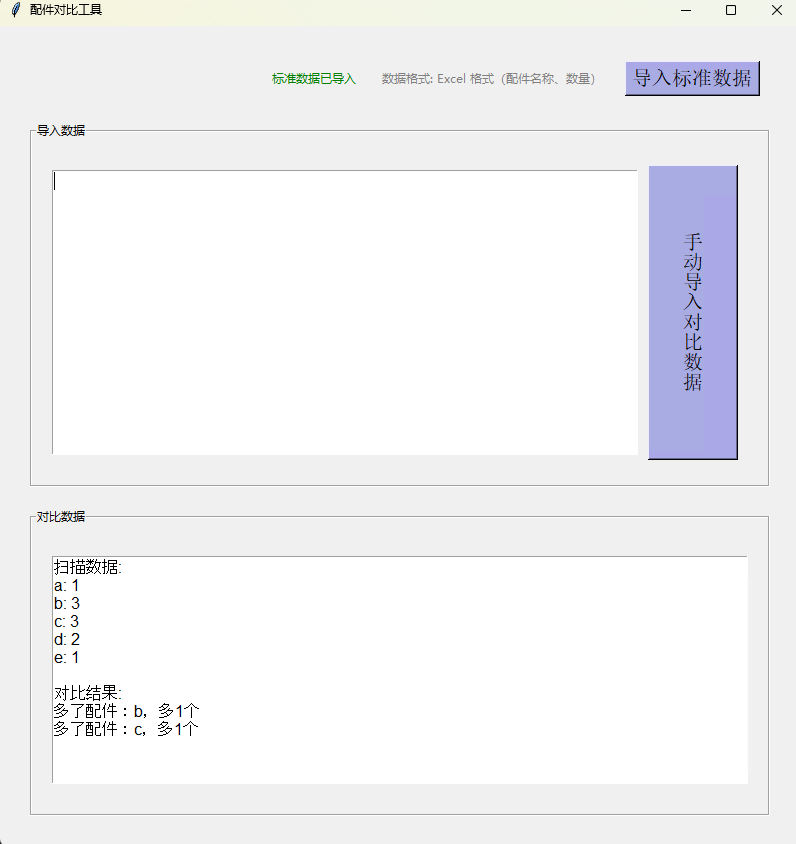
题目链接
https://www.luogu.com.cn/problem/P3823
分析
先解决队伍的合并与分离问题。使用链表结构,分别维护每只蚯蚓的前驱和后继即可。
然后考虑如何统计答案。可以对每只蚯蚓的“向后 \(k\) 数字串”使用字符串哈希的方式获得哈希值,再用一个哈希表存储每个哈希值出现的次数。对于给定的数字串 \(s\) 的每个长度为 \(k\) 的连续子串 \(t\),\(f(t)\) 即为 \(t\) 的哈希值在哈希表中出现的次数。
最后考虑维护每只蚯蚓的“向后 \(k\) 数字串”。
- 当 \(k=1\) 时,每只蚯蚓的“向后 \(k\) 数字串”是它的长度。
- 当 \(k \ge 2\) 时,每只蚯蚓的“向后 \(k\) 数字串”只有经历蚯蚓队伍的合并才会形成,只有经历蚯蚓队伍的分离才会消失(即队伍合并是数字串产生的必要不充分条件,队伍分离是数字串消失的必要不充分条件)。具体地,当进行队伍的合并操作时,对于前方队伍中的任何一只蚯蚓,若它的“向后 \(k\) 数字串”跨越了两个队伍,则这条数字串因此次合并而产生,将这个数字串的哈希值在哈希表中的出现次数 \(+1\) 即可。队伍的分离操作同理。
细节内容见代码注释。
Code
#include<bits/stdc++.h>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/hash_policy.hpp>
#define i64 long long
#define uns unsignedusing namespace std;
using namespace __gnu_pbds;constexpr int N=2e5+5;
int n,m;
char s[int(1e7)+5];namespace Solve{//unordered_map 太慢,使用 pbds 的哈希表 gp_hash_table<uns i64,int>ght;//字符串哈希 constexpr uns i64 p=131;uns i64 pw[int(1e7+5)],hsh[int(1e7+5)];//预处理 void init_pw(int n){pw[0]=1;for(int i=1;i<=n;++i)pw[i]=pw[i-1]*p;return;}//对整个数字串进行哈希 void make_hash(int n,char *s,uns i64 *hash_table){for(int i=1;i<=n;++i)hash_table[i]=hash_table[i-1]*p+s[i]-48;return;}//获取子串的哈希值 uns i64 ask_hash(int l,int r,uns i64 *hash_table){if(l>r)return 0;return hash_table[r]-hash_table[l-1]*pw[r-l+1];}//链表 struct Node{int pre,nxt;//指针域,前驱和后继 int dat;//数据域,蚯蚓的长度 }L[N];//合并 void Union(int p1,int p2){//更新指针 L[p1].nxt=p2,L[p2].pre=p1;//由于题目中 k<=50,拥有跨越两个队伍的数字串的蚯蚓一定不超过 50 个 for(int i=p1,cnt_i=50;(~i)&&(cnt_i)!=0;i=L[i].pre,--cnt_i){uns i64 num_str=0ull;bool flg=false;//数字串长度不超过 50 for(int j=i,cnt_j=50;(~j)&&(cnt_j)!=0;j=L[j].nxt,--cnt_j){num_str=num_str*p+L[j].dat;if(j==p2)flg=true;//开始跨越两个队伍 if(flg)++ght[num_str];}}return;}//分离 void Cut(int p1){int p2=L[p1].nxt;for(int i=p1,cnt_i=50;(~i)&&(cnt_i)!=0;i=L[i].pre,--cnt_i){uns i64 num_str=0ull;bool flg=false;for(int j=i,cnt_j=50;(~j)&&(cnt_j)!=0;j=L[j].nxt,--cnt_j){num_str=num_str*p+L[j].dat;if(j==p2)flg=true;if(flg)--ght[num_str];}}//注意,由于要更新跨越两队伍的数字串的信息,指针的更新要放在后面 L[p1].nxt=L[p2].pre=-1;return;}//统计答案 constexpr i64 mod=998244353;i64 ask_ans(int k,char *s){int len=strlen(s+1);make_hash(len,s,hsh);i64 ans=1;for(int i=k;i<=len;++i){ans=ans*ght[ask_hash(i-k+1,i,hsh)]%mod;if(ans==0)break;}return ans;}
}using namespace Solve;int main(){ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);init_pw(int(1e7));cin>>n>>m;//初始化 for(int i=1;i<=n;++i){cin>>L[i].dat;L[i].pre=L[i].nxt=-1,++ght[L[i].dat];}int op,x1,x2;for(int id_op=1;id_op<=m;++id_op){cin>>op;if(op==1){cin>>x1>>x2;Union(x1,x2);}else if(op==2){cin>>x1;Cut(x1);}else{cin>>(s+1)>>x1;cout<<ask_ans(x1,s)<<'\n';}}return 0;
}