🌈个人主页: Aileen_0v0
🔥热门专栏: 华为鸿蒙系统学习|计算机网络|数据结构与算法
💫个人格言:"没有罗马,那就自己创造罗马~"
目录
Shell method
Setting up the Integral
例题
Example 1:
Example 2:
Example 3:

Computing volumes for solids of revolution using cylindrical shells(利用柱壳法计算旋转体体积):
Shell method
柱壳法对于旋转固体体积的计算公式如下:
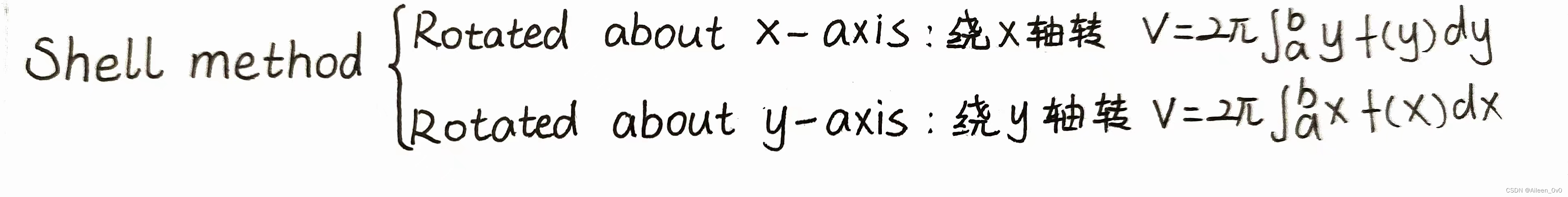
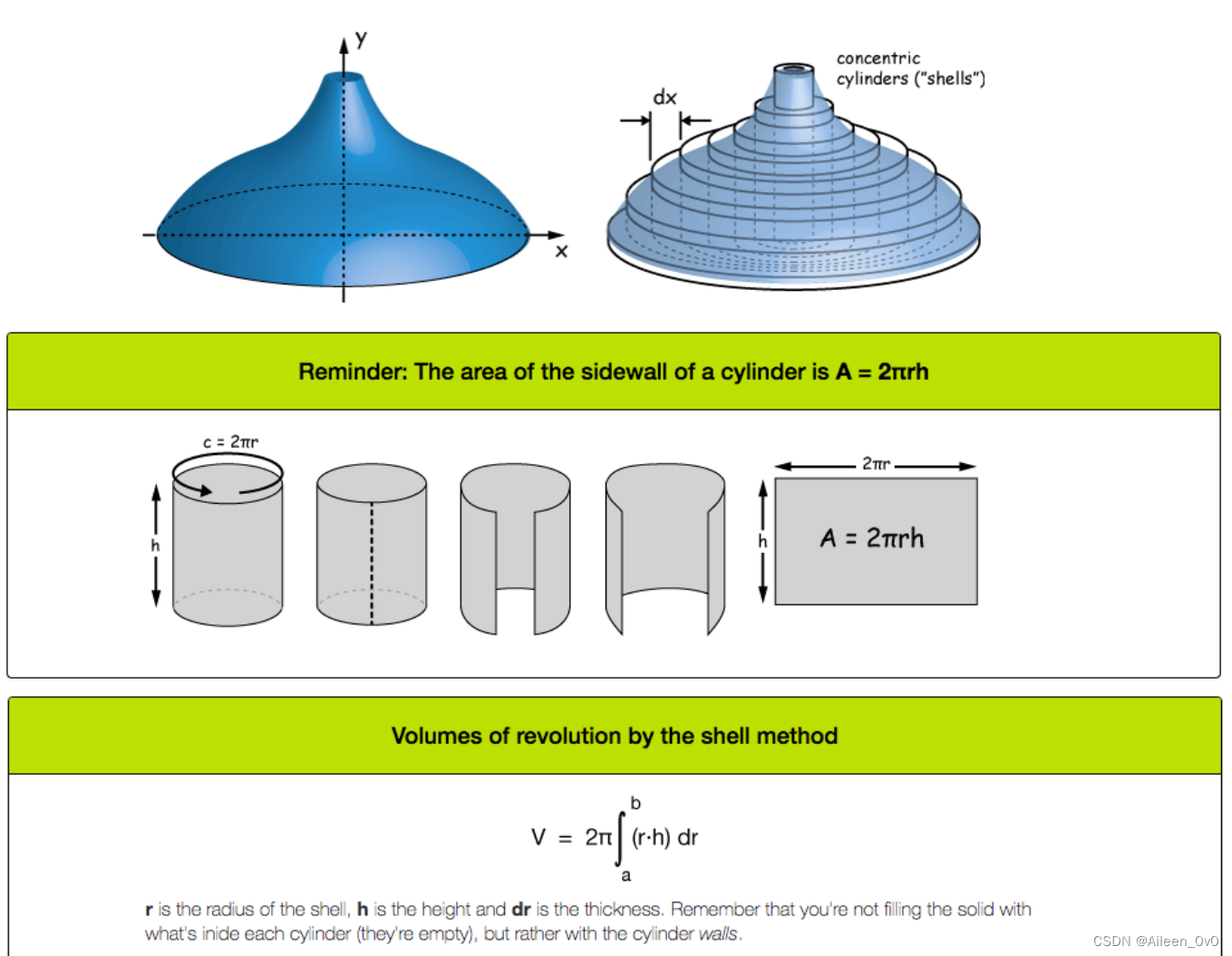
Setting up the Integral
• Keypoints:
1. When using cylindrical shells, you integrate with respect to the variable that is perpendicular to the axis of rotation.(使用柱壳法时,可以相对于垂直于旋转轴的变量进行积分)
2. The integral can be set up as 2π ∫(a to b) r(x) h(x) dx or 2π ∫(c to d) r(y) h(y) dy , depending on the orientation.
例题
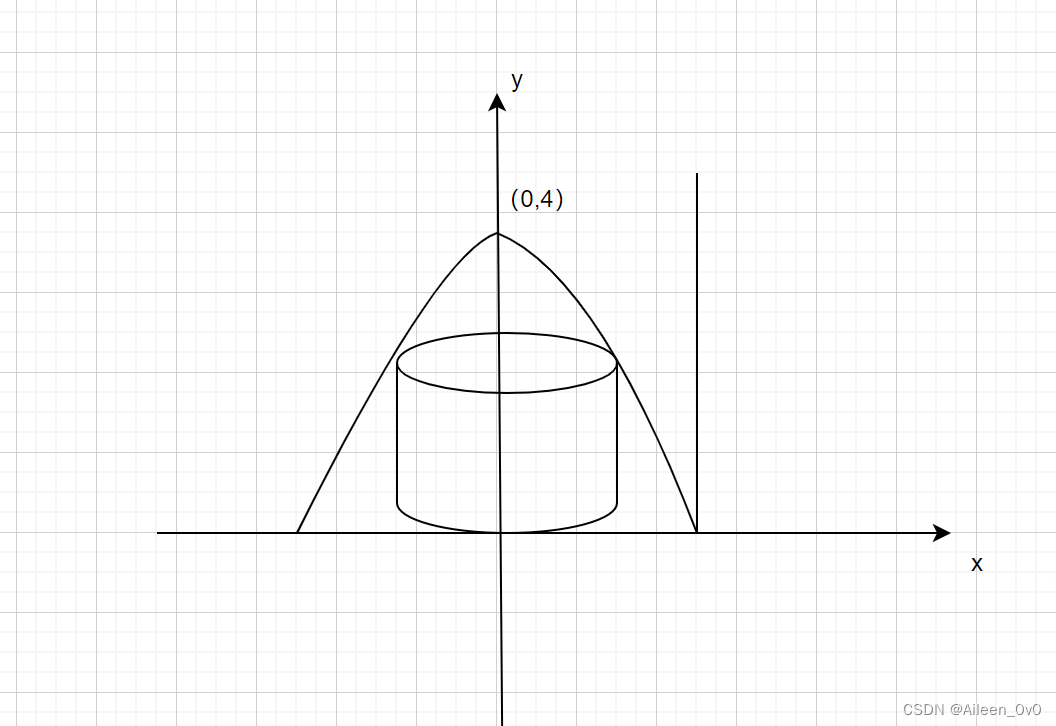
Example 1:
Use the shell method to find the volume of the solid generated by revolving the shaded region about the y-axis.
Limit is 0<x<pi

Example 2:
Use the shell method to find the volume of the solid generated by revolving the shaded region about the x-axis.
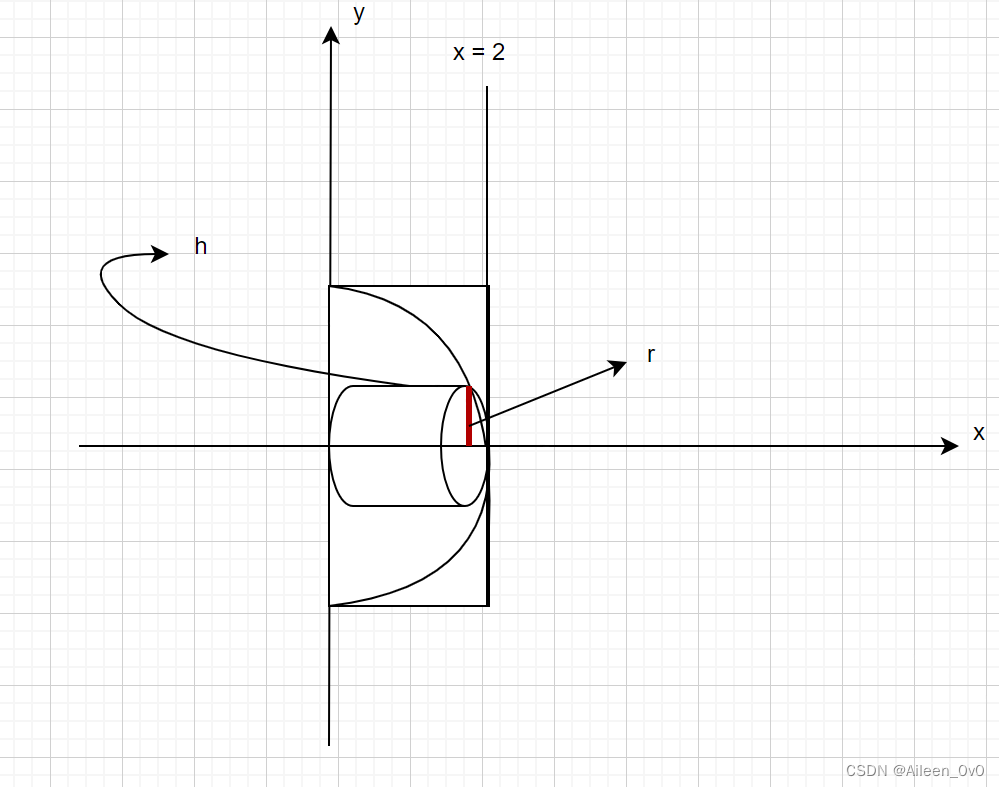
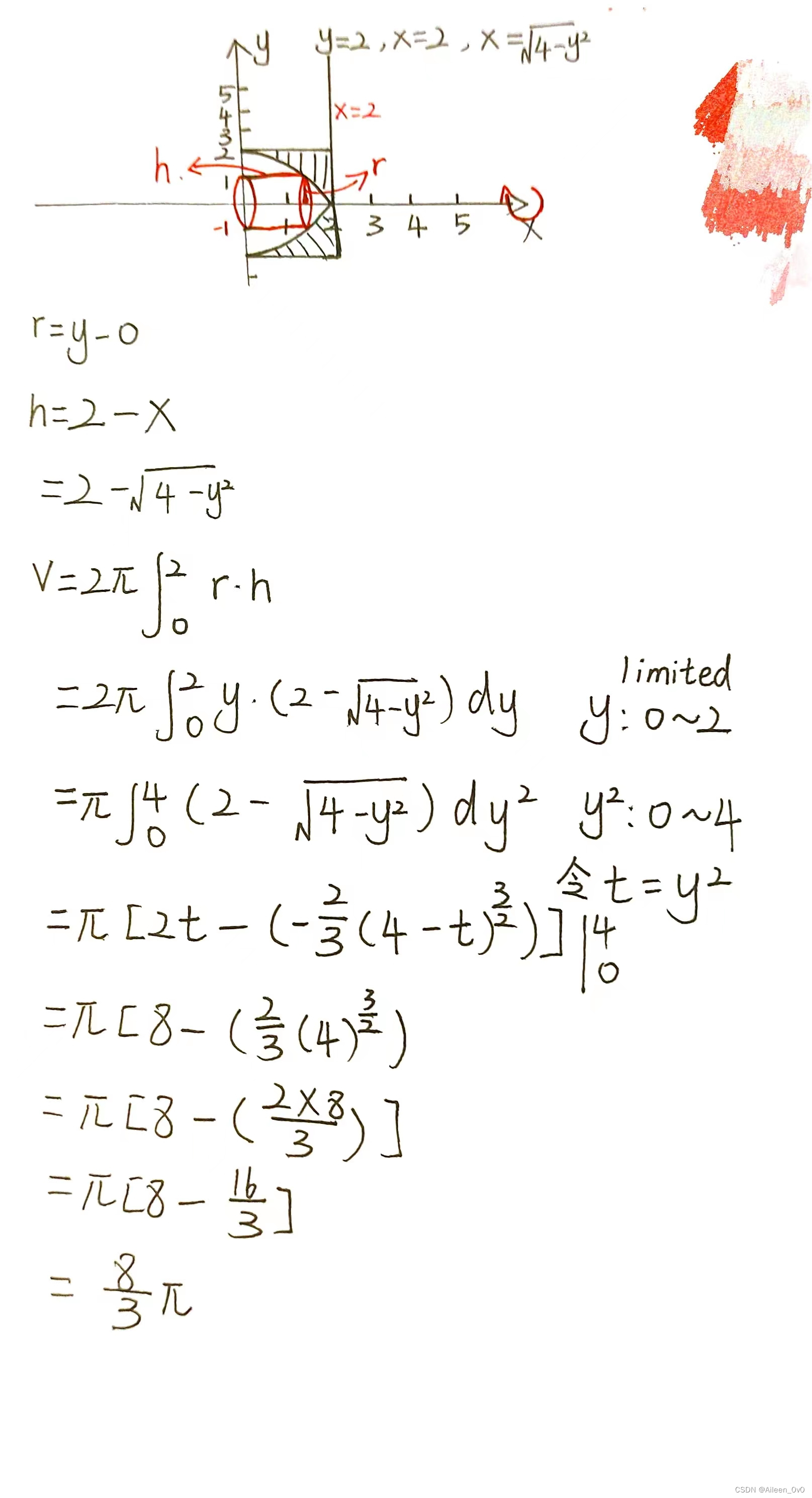
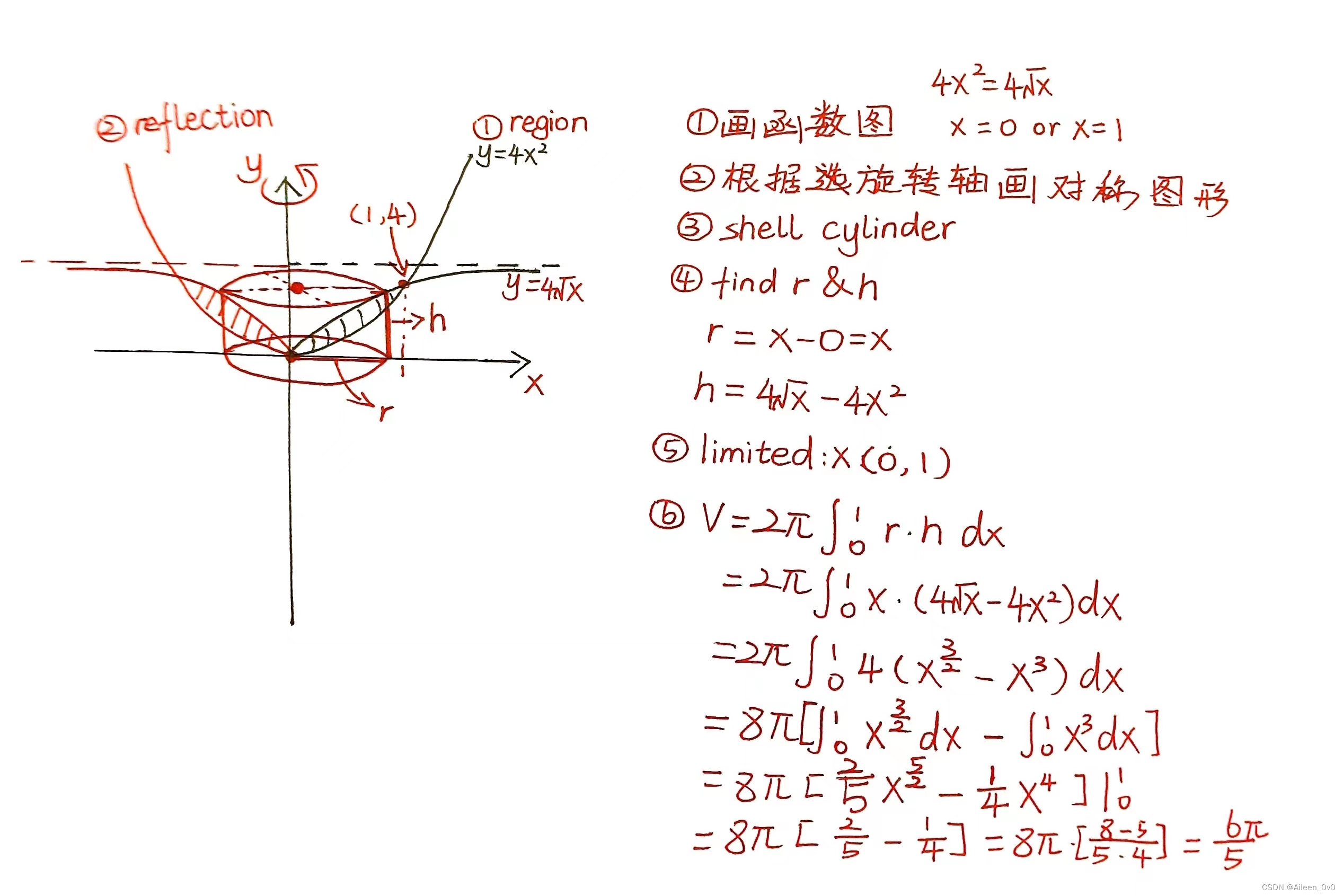
Example 3:
Use the shell method to find the volume of the solid generated by revolving the region bounded by the given curves and lines about the y-axis.