🦄个人主页:修修修也
🎏所属专栏:数据结构
⚙️操作环境:Visual Studio 2022

目录
📌二叉树的定义
📌二叉树的特点
📌特殊二叉树
📌二叉树的性质
📌二叉树的存储结构
📌二叉树的遍历
前序遍历
中序遍历
后序遍历
层序遍历
结语
📌二叉树的定义
二叉树(Binary Tree)是n(n≥0)个结点的有限集合,该集合或者为空集(称为空二叉树),或者由一个根结点和两颗互不相交的,分别称为根结点的左子树和右子树的二叉树组成.
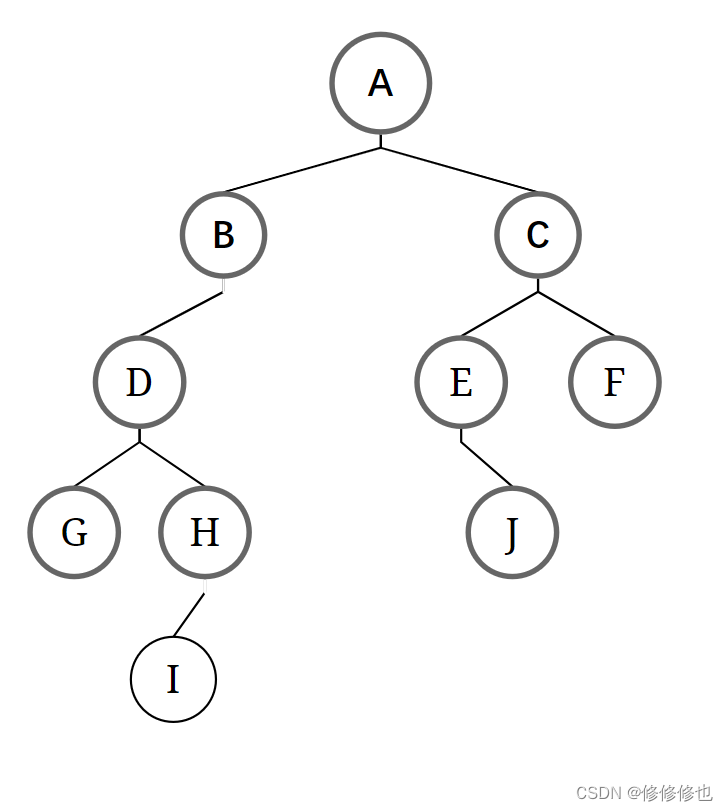
二叉树逻辑结构如下图所示:
📌二叉树的特点
二叉树的特点有:
- 每个结点最多有两棵子树,所以二叉树中不存在度大于2的结点.注意不是只有两颗子树,而是最多有.没有子树或者有一颗子树都是可以的.
- 左子树和右子树是有顺序的,次序不能任意颠倒.
- 即使树中某个结点只有一棵子树,也要区分它是左子树还是右子树.下图中树1和树2是同一颗树,但它们却是不同的二叉树:
二叉树具有五种基本形态:
- 空二叉树.
- 只有一个根结点.
- 根结点只有左子树.
- 根结点只有右子树.
- 根结点既有左子树又有右子树.
只有三个结点的二叉树,有几种形态?
答案是有以下5种形态:
📌特殊二叉树
- 斜树
所有的结点都只有左子树的二叉树叫左斜树.所有结点都是只有右子树的二叉树叫右斜树.这两者统称为斜树.上图中的树2就是左斜树,树3就是右斜树.
斜树每一层只有一个结点,结点的个数与二叉树的深度相同.
- 满二叉树
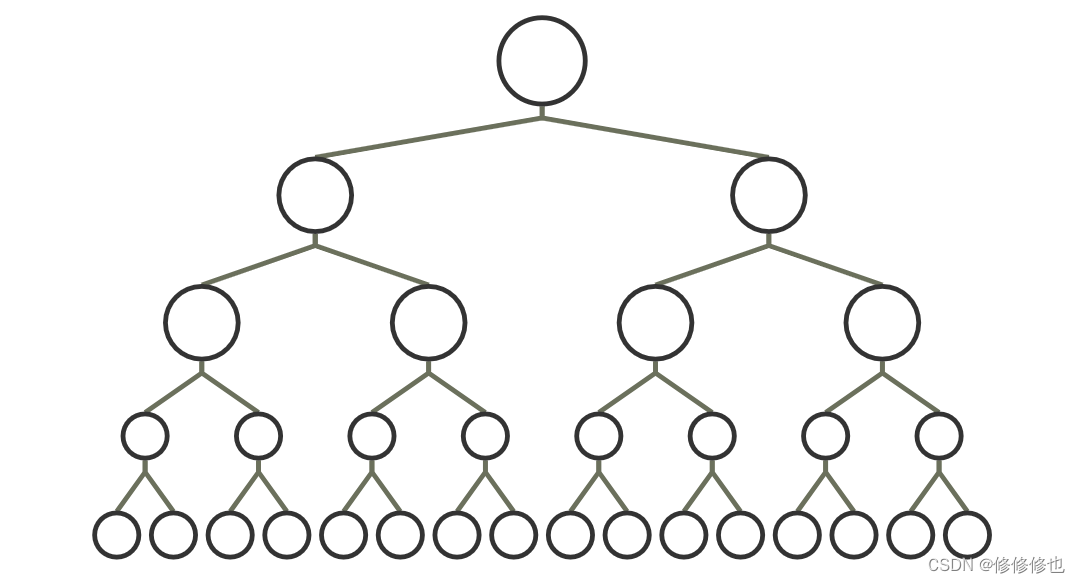
在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树.
如下图所示,该树就是一颗满二叉树:
注意,单是每个结点都存在左右子树,不能算是满二叉树,还必须要所有的叶子都在同一层上,这就做到了整棵树的平衡.
因此,满二叉树的特点有:
- 叶子只能出现在最下一层.出现在其他层就不可能达成平衡.
- 非叶子节点的度一定是2.
- 在同样深度的二叉树中,满二叉树的结点个数最多,叶子数最多.
- 完全二叉树
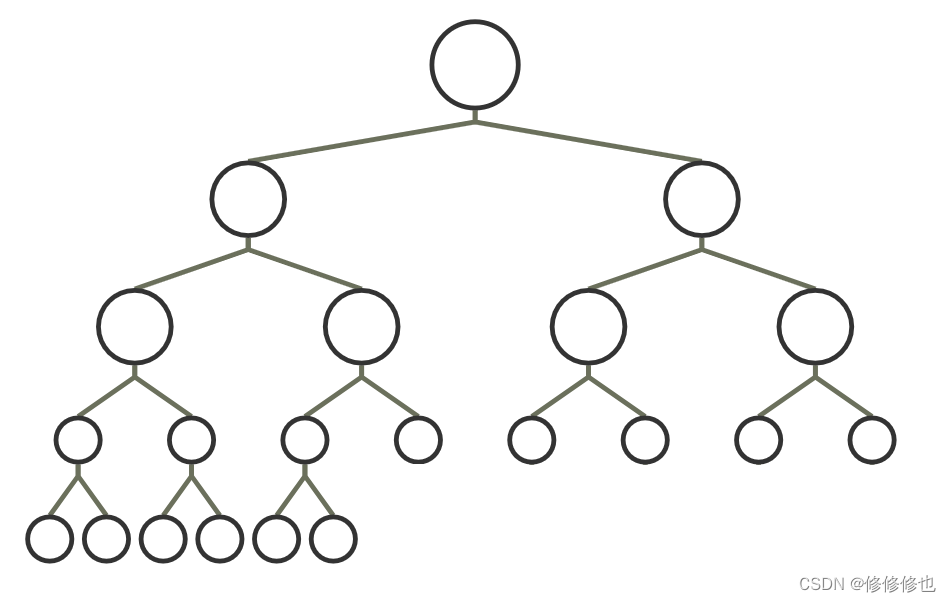
对一颗具有n个结点的二叉树按层序编号,如果编号为i(1≤i≤n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同,则这颗二叉树称为完全二叉树,如下图所示:
完全二叉树的特点有:
- 叶子结点只能出现在最下两层.
- 最下层的叶子一定集中在左部连续位置.
- 倒数二层,若有叶子结点,一定都在右部连续位置.
- 如果结点度为1,则该结点只有左孩子,即不存在只有右子树的情况.
- 同样结点数的二叉树,完全二叉树的深度最小.
📌二叉树的性质
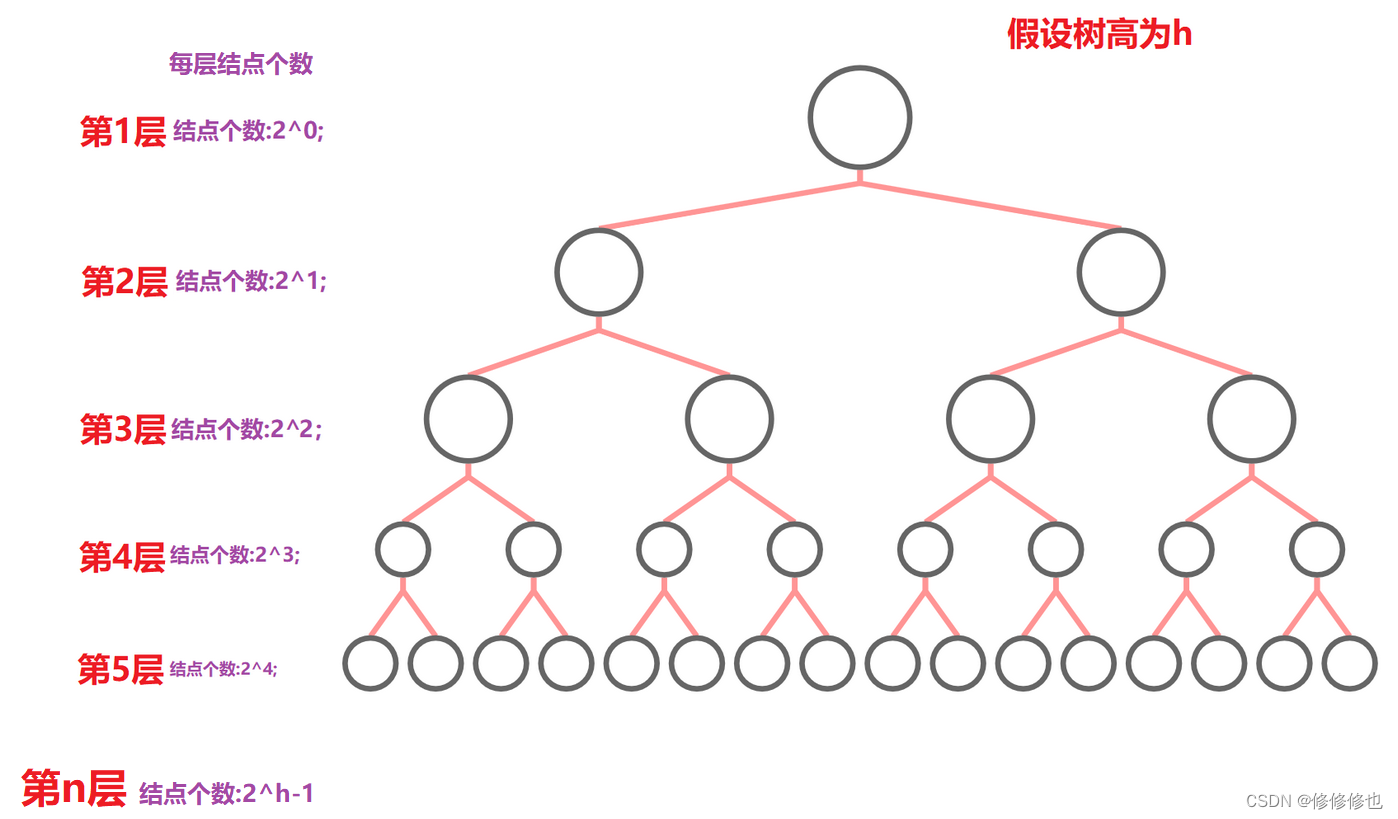
性质1:
在二叉树的第i层上至多有
个结点(i≥1).
推导如下:
性质2:
深度为k的二叉树至多有
个结点(k≥1).
推导如下:
性质3:
对任何一颗二叉树T,如果其终端结点数为,度为2的结点数为
,则
.
终端结点数其实就是叶子节点数,一颗二叉树,只会存在度为0,度为1,度为2的结点,我们假设度为1的节点数为
,则树T结点总数
.
性质4:
具有n个结点的完全二叉树的深度为
, (
表示不大于x的最大整数).
我们由满二叉树的定义可知,深度为k的满二叉树的结点数n一定是
.因为这是最多的结点个数.那么对于
倒推可得满二叉树的深度数为
.
而对于完全二叉树而言,它的节点数一定少于等于同样深度数的满二叉树的结点数
,但一定多于
.即满足
.易推导得
.
性质5:
如果对一颗有n个结点的完全二叉树(其深度为
)的结点按层序编号(从第1层到第
层,每层从左到右),对任一结点i(1≤i≤n)有:
- 如果i=1,则结点i是二叉树的根,无双亲;如果i>1,则其双亲是结点
.
- 如果2*i>n,则结点i无左孩子(结点i为叶子结点);否则其左孩子是结点2*i.
- 如果2*i+1>n,则结点i无右孩子;否则其右孩子是结点2*i+1.
📌二叉树的存储结构
- 顺序存储结构
二叉树的顺序存储结构就是用一维数组存储二叉树中的结点,并且结点的存储位置,也就是数组的下标要能体现结点之间的逻辑关系.
先来看看完全二叉树的顺序存储,一颗完全二叉树如下图:
将这颗二叉树存到数组中,相应的下标对应其同样的位置:
但如果遇到树中不存在的结点,我们也可在顺序结构中存入"^"或空,来表示该结点不存在:
这种顺序存储结构仅适用于完全二叉树.因为,在最坏的情况下,一个深度为k且只有k个结点的单支树(即树中不存在度为2的结点)却需要长度为
的一维数组:
- 二叉链表
因为二叉树每个结点最多有两个孩子,所以为它的结点设计一个数据域和两个指针域,分别指向两个孩子,我们称这样的链表叫做二叉链表.
结点结构图如下:
二叉链表结构定义代码如下:
typedef struct BiTNode {TElemType data; //数据域struct BiTNode*left; //左孩子指针域struct BiTNode*right; //右孩子指针域 }BiTNode;
📌二叉树的遍历
二叉树的遍历(traversing binary tree)是指从根节点出发,按照某种次序依次访问二叉树中所有结点,使得每个结点被访问一次且只访问一次.
前序遍历
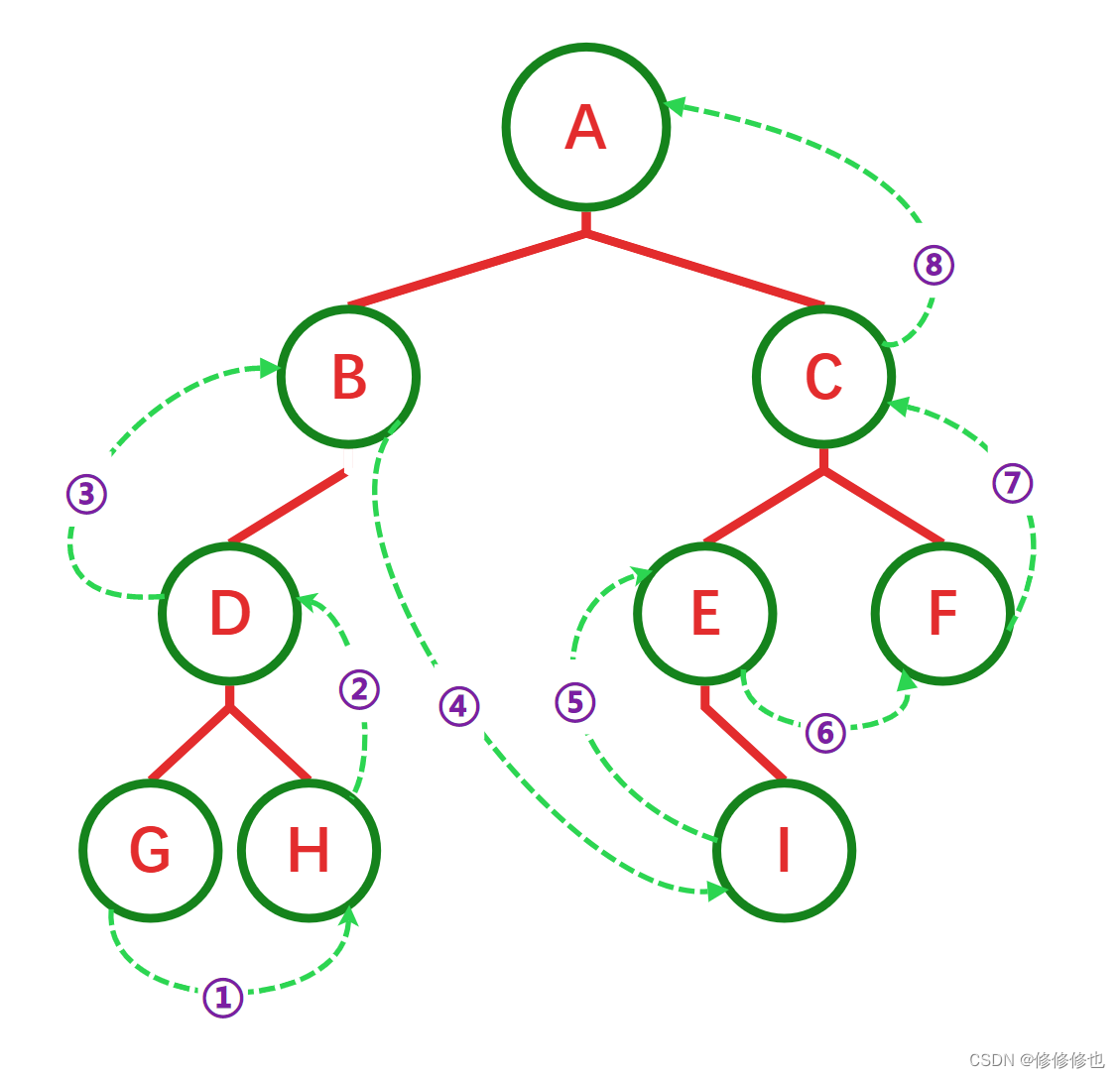
前序遍历的规则是:若二叉树为空,则空操作返回,否则先访问根节点,然后前序遍历左子树,再前序遍历右子树.
如下图所示,遍历的顺序为:ABDGHCEIF
中序遍历
中序遍历的规则是:若二叉树为空,则空操作返回,否则从根节点开始(注意不是先访问根节点)先中序遍历根节点的左子树,然后访问根节点,最后中序遍历右子树.
如下图所示,遍历的顺序为:GDHBAEICF
后序遍历
后序遍历的规则是:若二叉树为空,则空操作返回,否则从左到右先叶子后结点的方式遍历访问左右子树,最后是访问根节点.
如下图所示,遍历的顺序为:GHDBIEFCA
层序遍历
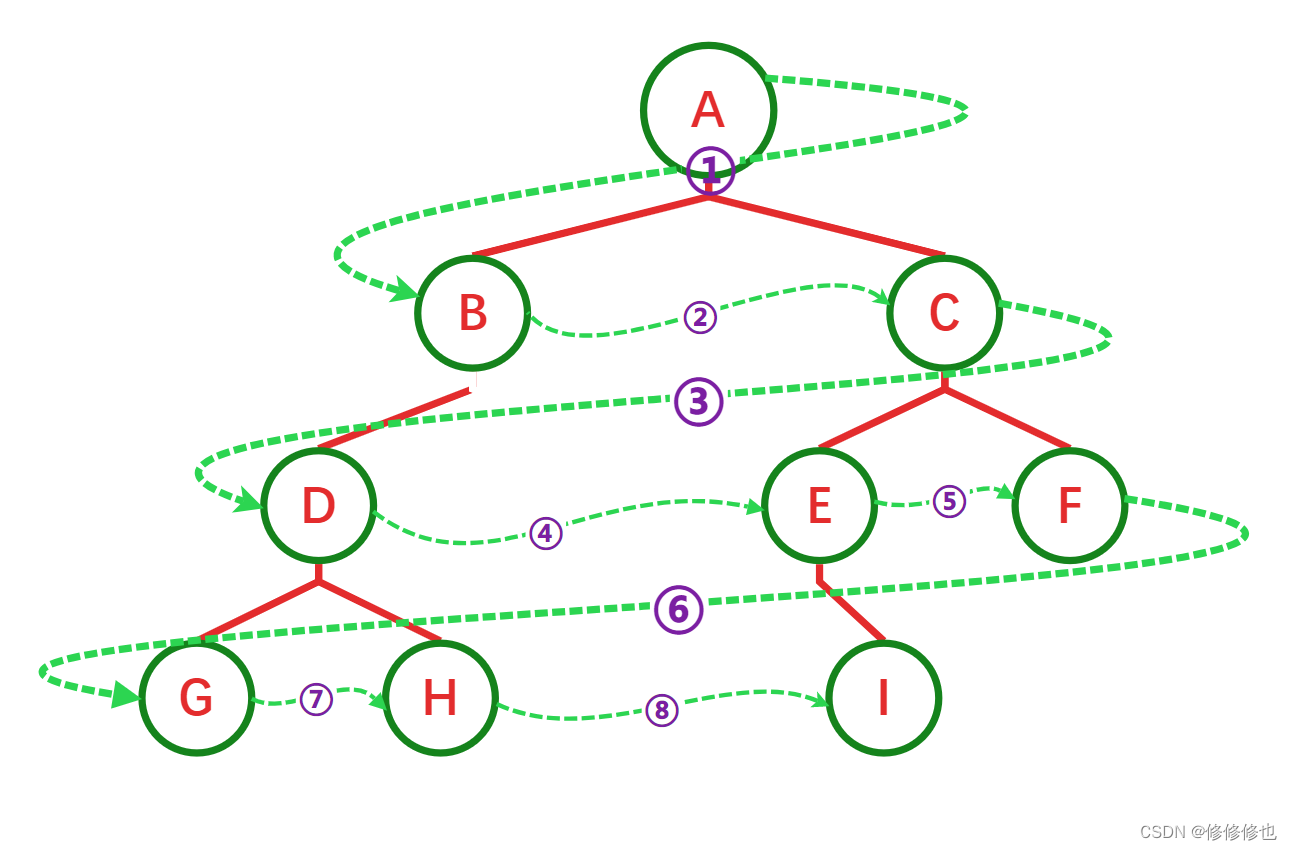
层序遍历的规则是:若二叉树为空,则空操作返回,否则从树的第一层,也就是根节点开始访问,从上而下逐层遍历,在同一层中,按从左到右的顺序对结点逐个访问.
如下图所示,遍历的顺序为:ABCDEFGHI
结语
希望这篇二叉树的介绍能对大家有所帮助,欢迎大佬们留言或私信与我交流.
学海漫浩浩,我亦苦作舟!关注我,大家一起学习,一起进步!
相关文章推荐
【数据结构】什么是树?
【数据结构】什么是线性表?
【数据结构】什么是栈?
【数据结构】用C语言实现顺序栈(附完整运行代码)
【数据结构】深入浅出理解链表中二级指针的应用
【数据结构】10道经典面试题目带你玩转链表