目录
编程实现优化算法,并3D可视化
1. 函数3D可视化
2.加入优化算法,画出轨迹
3.复现CS231经典动画
4.结合3D动画,用自己的语言,从轨迹、速度等多个角度讲解各个算法优缺点
5.总结
编程实现优化算法,并3D可视化
1. 函数3D可视化
分别画出 和
的3D图
import torch
import numpy as np
import matplotlib.pyplot as pltclass Op(object):def __init__(self):passdef __call__(self, inputs):return self.forward(inputs)# 输入:张量inputs# 输出:张量outputsdef forward(self, inputs):# return outputsraise NotImplementedError# 输入:最终输出对outputs的梯度outputs_grads# 输出:最终输出对inputs的梯度inputs_gradsdef backward(self, outputs_grads):# return inputs_gradsraise NotImplementedErrorclass OptimizedFunction3D(Op):def __init__(self):super(OptimizedFunction3D, self).__init__()self.params = {'x': 0}self.grads = {'x': 0}def forward(self, x):self.params['x'] = xreturn x[0] ** 2 + x[1] ** 2 + x[1] ** 3 + x[0] * x[1]def backward(self):x = self.params['x']gradient1 = 2 * x[0] + x[1]gradient2 = 2 * x[1] + 3 * x[1] ** 2 + x[0]grad1 = torch.Tensor([gradient1])grad2 = torch.Tensor([gradient2])self.grads['x'] = torch.cat([grad1, grad2])x1 = np.arange(-3, 3, 0.1)
x2 = np.arange(-3, 3, 0.1)
x1, x2 = np.meshgrid(x1, x2)
init_x = torch.Tensor(np.array([x1, x2]))model = OptimizedFunction3D()# 绘制 f_3d函数 的 三维图像
fig = plt.figure()
ax = plt.axes(projection='3d')X = init_x[0].numpy()
Y = init_x[1].numpy()
Z = model(init_x).numpy() # 改为 model(init_x).numpy() David 2022.12.4
ax.plot_surface(X, Y, Z, cmap='rainbow')ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel('f(x1,x2)')
plt.show()
结果如下:

import torch
import numpy as np
import matplotlib.pyplot as pltclass Op(object):def __init__(self):passdef __call__(self, inputs):return self.forward(inputs)# 输入:张量inputs# 输出:张量outputsdef forward(self, inputs):# return outputsraise NotImplementedError# 输入:最终输出对outputs的梯度outputs_grads# 输出:最终输出对inputs的梯度inputs_gradsdef backward(self, outputs_grads):# return inputs_gradsraise NotImplementedErrorclass OptimizedFunction3D(Op):def __init__(self):super(OptimizedFunction3D, self).__init__()self.params = {'x': 0}self.grads = {'x': 0}def forward(self, x):self.params['x'] = xreturn x[0] ** 2 / 20 + x[1] ** 2def backward(self):x = self.params['x']gradient1 = 2 * x[0] + x[1]gradient2 = 2 * x[1] + 3 * x[1] ** 2 + x[0]grad1 = torch.Tensor([gradient1])grad2 = torch.Tensor([gradient2])self.grads['x'] = torch.cat([grad1, grad2])x1 = np.arange(-40, 40, 0.1)
x2 = np.arange(-40, 40, 0.1)
x1, x2 = np.meshgrid(x1, x2)
init_x = torch.Tensor(np.array([x1, x2]))model = OptimizedFunction3D()# 绘制 f_3d函数 的 三维图像
fig = plt.figure()
ax = plt.axes(projection='3d')X = init_x[0].numpy()
Y = init_x[1].numpy()
Z = model(init_x).numpy() # 改为 model(init_x).numpy() David 2022.12.4
ax.plot_surface(X, Y, Z, cmap='rainbow')ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel('f(x1,x2)')
plt.show()
结果如下:
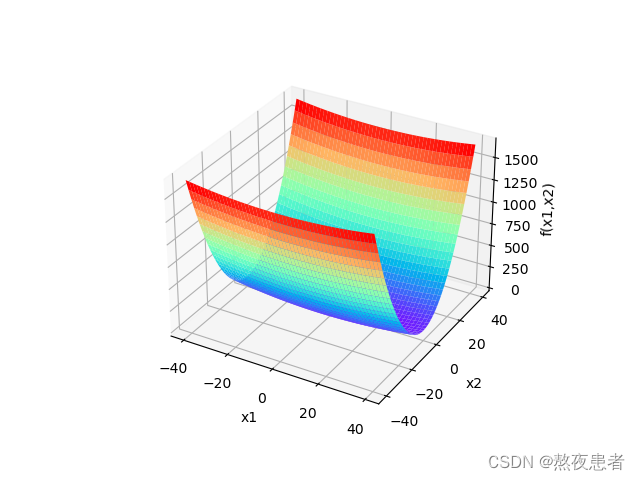
2.加入优化算法,画出轨迹
分别画出 和
的3D轨迹图
结合3D动画,用自己的语言,从轨迹、速度等多个角度讲解各个算法优缺点
import torch
import numpy as np
import copy
from matplotlib import pyplot as plt
from matplotlib import animation
from itertools import zip_longestclass Op(object):def __init__(self):passdef __call__(self, inputs):return self.forward(inputs)# 输入:张量inputs# 输出:张量outputsdef forward(self, inputs):# return outputsraise NotImplementedError# 输入:最终输出对outputs的梯度outputs_grads# 输出:最终输出对inputs的梯度inputs_gradsdef backward(self, outputs_grads):# return inputs_gradsraise NotImplementedErrorclass Optimizer(object): # 优化器基类def __init__(self, init_lr, model):"""优化器类初始化"""# 初始化学习率,用于参数更新的计算self.init_lr = init_lr# 指定优化器需要优化的模型self.model = modeldef step(self):"""定义每次迭代如何更新参数"""passclass SimpleBatchGD(Optimizer):def __init__(self, init_lr, model):super(SimpleBatchGD, self).__init__(init_lr=init_lr, model=model)def step(self):# 参数更新if isinstance(self.model.params, dict):for key in self.model.params.keys():self.model.params[key] = self.model.params[key] - self.init_lr * self.model.grads[key]class Adagrad(Optimizer):def __init__(self, init_lr, model, epsilon):"""Adagrad 优化器初始化输入:- init_lr: 初始学习率 - model:模型,model.params存储模型参数值 - epsilon:保持数值稳定性而设置的非常小的常数"""super(Adagrad, self).__init__(init_lr=init_lr, model=model)self.G = {}for key in self.model.params.keys():self.G[key] = 0self.epsilon = epsilondef adagrad(self, x, gradient_x, G, init_lr):"""adagrad算法更新参数,G为参数梯度平方的累计值。"""G += gradient_x ** 2x -= init_lr / torch.sqrt(G + self.epsilon) * gradient_xreturn x, Gdef step(self):"""参数更新"""for key in self.model.params.keys():self.model.params[key], self.G[key] = self.adagrad(self.model.params[key],self.model.grads[key],self.G[key],self.init_lr)class RMSprop(Optimizer):def __init__(self, init_lr, model, beta, epsilon):"""RMSprop优化器初始化输入:- init_lr:初始学习率- model:模型,model.params存储模型参数值- beta:衰减率- epsilon:保持数值稳定性而设置的常数"""super(RMSprop, self).__init__(init_lr=init_lr, model=model)self.G = {}for key in self.model.params.keys():self.G[key] = 0self.beta = betaself.epsilon = epsilondef rmsprop(self, x, gradient_x, G, init_lr):"""rmsprop算法更新参数,G为迭代梯度平方的加权移动平均"""G = self.beta * G + (1 - self.beta) * gradient_x ** 2x -= init_lr / torch.sqrt(G + self.epsilon) * gradient_xreturn x, Gdef step(self):"""参数更新"""for key in self.model.params.keys():self.model.params[key], self.G[key] = self.rmsprop(self.model.params[key],self.model.grads[key],self.G[key],self.init_lr)class Momentum(Optimizer):def __init__(self, init_lr, model, rho):"""Momentum优化器初始化输入:- init_lr:初始学习率- model:模型,model.params存储模型参数值- rho:动量因子"""super(Momentum, self).__init__(init_lr=init_lr, model=model)self.delta_x = {}for key in self.model.params.keys():self.delta_x[key] = 0self.rho = rhodef momentum(self, x, gradient_x, delta_x, init_lr):"""momentum算法更新参数,delta_x为梯度的加权移动平均"""delta_x = self.rho * delta_x - init_lr * gradient_xx += delta_xreturn x, delta_xdef step(self):"""参数更新"""for key in self.model.params.keys():self.model.params[key], self.delta_x[key] = self.momentum(self.model.params[key],self.model.grads[key],self.delta_x[key],self.init_lr)class Nesterov(Optimizer):def __init__(self, init_lr, model, rho):super(Nesterov, self).__init__(init_lr=init_lr, model=model)self.delta_x = {}for key in self.model.params.keys():self.delta_x[key] = 0self.rho = rhodef nesterov(self, x, gradient_x, delta_x, init_lr):"""Nesterov算法更新参数,delta_x为梯度的加权移动平均"""delta_x_prev = delta_xdelta_x = self.rho * delta_x - init_lr * gradient_xx += -self.rho * delta_x_prev + (1 + self.rho) * delta_xreturn x, delta_xdef step(self):"""参数更新"""for key in self.model.params.keys():self.model.params[key], self.delta_x[key] = self.nesterov(self.model.params[key],self.model.grads[key],self.delta_x[key],self.init_lr)class Adam(Optimizer):def __init__(self, init_lr, model, beta1, beta2, epsilon):"""Adam优化器初始化输入:- init_lr:初始学习率- model:模型,model.params存储模型参数值- beta1, beta2:移动平均的衰减率- epsilon:保持数值稳定性而设置的常数"""super(Adam, self).__init__(init_lr=init_lr, model=model)self.beta1 = beta1self.beta2 = beta2self.epsilon = epsilonself.M, self.G = {}, {}for key in self.model.params.keys():self.M[key] = 0self.G[key] = 0self.t = 1def adam(self, x, gradient_x, G, M, t, init_lr):"""adam算法更新参数输入:- x:参数- G:梯度平方的加权移动平均- M:梯度的加权移动平均- t:迭代次数- init_lr:初始学习率"""M = self.beta1 * M + (1 - self.beta1) * gradient_xG = self.beta2 * G + (1 - self.beta2) * gradient_x ** 2M_hat = M / (1 - self.beta1 ** t)G_hat = G / (1 - self.beta2 ** t)t += 1x -= init_lr / torch.sqrt(G_hat + self.epsilon) * M_hatreturn x, G, M, tdef step(self):"""参数更新"""for key in self.model.params.keys():self.model.params[key], self.G[key], self.M[key], self.t = self.adam(self.model.params[key],self.model.grads[key],self.G[key],self.M[key],self.t,self.init_lr)class OptimizedFunction3D(Op):def __init__(self):super(OptimizedFunction3D, self).__init__()self.params = {'x': 0}self.grads = {'x': 0}def forward(self, x):self.params['x'] = xreturn x[0] ** 2 + x[1] ** 2 + x[1] ** 3 + x[0] * x[1]def backward(self):x = self.params['x']gradient1 = 2 * x[0] + x[1]gradient2 = 2 * x[1] + 3 * x[1] ** 2 + x[0]grad1 = torch.Tensor([gradient1])grad2 = torch.Tensor([gradient2])self.grads['x'] = torch.cat([grad1, grad2])class Visualization3D(animation.FuncAnimation):""" 绘制动态图像,可视化参数更新轨迹 """def __init__(self, *xy_values, z_values, labels=[], colors=[], fig, ax, interval=600, blit=True, **kwargs):"""初始化3d可视化类输入:xy_values:三维中x,y维度的值z_values:三维中z维度的值labels:每个参数更新轨迹的标签colors:每个轨迹的颜色interval:帧之间的延迟(以毫秒为单位)blit:是否优化绘图"""self.fig = figself.ax = axself.xy_values = xy_valuesself.z_values = z_valuesframes = max(xy_value.shape[0] for xy_value in xy_values)self.lines = [ax.plot([], [], [], label=label, color=color, lw=2)[0]for _, label, color in zip_longest(xy_values, labels, colors)]super(Visualization3D, self).__init__(fig, self.animate, init_func=self.init_animation, frames=frames,interval=interval, blit=blit, **kwargs)def init_animation(self):# 数值初始化for line in self.lines:line.set_data([], [])line.set_3d_properties(np.asarray([])) # 源程序中有这一行,加上会报错。 Edit by David 2022.12.4return self.linesdef animate(self, i):# 将x,y,z三个数据传入,绘制三维图像for line, xy_value, z_value in zip(self.lines, self.xy_values, self.z_values):line.set_data(xy_value[:i, 0], xy_value[:i, 1])line.set_3d_properties(z_value[:i])return self.linesdef train_f(model, optimizer, x_init, epoch):x = x_initall_x = []losses = []for i in range(epoch):all_x.append(copy.deepcopy(x.numpy())) # 浅拷贝 改为 深拷贝, 否则List的原值会被改变。 Edit by David 2022.12.4.loss = model(x)losses.append(loss)model.backward()optimizer.step()x = model.params['x']return torch.Tensor(np.array(all_x)), losses# 构建5个模型,分别配备不同的优化器
model1 = OptimizedFunction3D()
opt_gd = SimpleBatchGD(init_lr=0.01, model=model1)model2 = OptimizedFunction3D()
opt_adagrad = Adagrad(init_lr=0.5, model=model2, epsilon=1e-7)model3 = OptimizedFunction3D()
opt_rmsprop = RMSprop(init_lr=0.1, model=model3, beta=0.9, epsilon=1e-7)model4 = OptimizedFunction3D()
opt_momentum = Momentum(init_lr=0.01, model=model4, rho=0.9)model5 = OptimizedFunction3D()
opt_adam = Adam(init_lr=0.1, model=model5, beta1=0.9, beta2=0.99, epsilon=1e-7)model6 = OptimizedFunction3D()
opt_nesterov = Nesterov(init_lr=0.01, model=model6, rho=0.9)models = [model1, model2, model3, model4, model5, model6]
opts = [opt_gd, opt_adagrad, opt_rmsprop, opt_momentum, opt_adam, opt_nesterov]x_all_opts = []
z_all_opts = []# 使用不同优化器训练for model, opt in zip(models, opts):x_init = torch.FloatTensor([2, 3])x_one_opt, z_one_opt = train_f(model, opt, x_init, 150) # epoch# 保存参数值x_all_opts.append(x_one_opt.numpy())z_all_opts.append(np.squeeze(z_one_opt))# 使用numpy.meshgrid生成x1,x2矩阵,矩阵的每一行为[-3, 3],以0.1为间隔的数值
x1 = np.arange(-3, 3, 0.1)
x2 = np.arange(-3, 3, 0.1)
x1, x2 = np.meshgrid(x1, x2)
init_x = torch.Tensor(np.array([x1, x2]))model = OptimizedFunction3D()# 绘制 f_3d函数 的 三维图像
fig = plt.figure()
ax = plt.axes(projection='3d')X = init_x[0].numpy()
Y = init_x[1].numpy()
Z = model(init_x).numpy() # 改为 model(init_x).numpy() David 2022.12.4
ax.plot_surface(X, Y, Z, cmap='rainbow')ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel('f(x1,x2)')
labels = ['SGD', 'AdaGrad', 'RMSprop', 'Momentum', 'Adam', 'Nesterov']
colors = ['#f6373c', '#f6f237', '#45f637', '#37f0f6', '#000000', '#FED295']animator = Visualization3D(*x_all_opts, z_values=z_all_opts, labels=labels, colors=colors, fig=fig, ax=ax)ax.legend(loc='upper left')
animator.save('animation.gif', writer='ffmpeg')
plt.show()
输出结果:

import torch
import numpy as np
import copy
from matplotlib import pyplot as plt
from matplotlib import animation
from itertools import zip_longest
from matplotlib import cmclass Op(object):def __init__(self):passdef __call__(self, inputs):return self.forward(inputs)# 输入:张量inputs# 输出:张量outputsdef forward(self, inputs):# return outputsraise NotImplementedError# 输入:最终输出对outputs的梯度outputs_grads# 输出:最终输出对inputs的梯度inputs_gradsdef backward(self, outputs_grads):# return inputs_gradsraise NotImplementedErrorclass Optimizer(object): # 优化器基类def __init__(self, init_lr, model):"""优化器类初始化"""# 初始化学习率,用于参数更新的计算self.init_lr = init_lr# 指定优化器需要优化的模型self.model = modeldef step(self):"""定义每次迭代如何更新参数"""passclass SimpleBatchGD(Optimizer):def __init__(self, init_lr, model):super(SimpleBatchGD, self).__init__(init_lr=init_lr, model=model)def step(self):# 参数更新if isinstance(self.model.params, dict):for key in self.model.params.keys():self.model.params[key] = self.model.params[key] - self.init_lr * self.model.grads[key]class Adagrad(Optimizer):def __init__(self, init_lr, model, epsilon):"""Adagrad 优化器初始化输入:- init_lr: 初始学习率 - model:模型,model.params存储模型参数值 - epsilon:保持数值稳定性而设置的非常小的常数"""super(Adagrad, self).__init__(init_lr=init_lr, model=model)self.G = {}for key in self.model.params.keys():self.G[key] = 0self.epsilon = epsilondef adagrad(self, x, gradient_x, G, init_lr):"""adagrad算法更新参数,G为参数梯度平方的累计值。"""G += gradient_x ** 2x -= init_lr / torch.sqrt(G + self.epsilon) * gradient_xreturn x, Gdef step(self):"""参数更新"""for key in self.model.params.keys():self.model.params[key], self.G[key] = self.adagrad(self.model.params[key],self.model.grads[key],self.G[key],self.init_lr)class RMSprop(Optimizer):def __init__(self, init_lr, model, beta, epsilon):"""RMSprop优化器初始化输入:- init_lr:初始学习率- model:模型,model.params存储模型参数值- beta:衰减率- epsilon:保持数值稳定性而设置的常数"""super(RMSprop, self).__init__(init_lr=init_lr, model=model)self.G = {}for key in self.model.params.keys():self.G[key] = 0self.beta = betaself.epsilon = epsilondef rmsprop(self, x, gradient_x, G, init_lr):"""rmsprop算法更新参数,G为迭代梯度平方的加权移动平均"""G = self.beta * G + (1 - self.beta) * gradient_x ** 2x -= init_lr / torch.sqrt(G + self.epsilon) * gradient_xreturn x, Gdef step(self):"""参数更新"""for key in self.model.params.keys():self.model.params[key], self.G[key] = self.rmsprop(self.model.params[key],self.model.grads[key],self.G[key],self.init_lr)class Momentum(Optimizer):def __init__(self, init_lr, model, rho):"""Momentum优化器初始化输入:- init_lr:初始学习率- model:模型,model.params存储模型参数值- rho:动量因子"""super(Momentum, self).__init__(init_lr=init_lr, model=model)self.delta_x = {}for key in self.model.params.keys():self.delta_x[key] = 0self.rho = rhodef momentum(self, x, gradient_x, delta_x, init_lr):"""momentum算法更新参数,delta_x为梯度的加权移动平均"""delta_x = self.rho * delta_x - init_lr * gradient_xx += delta_xreturn x, delta_xdef step(self):"""参数更新"""for key in self.model.params.keys():self.model.params[key], self.delta_x[key] = self.momentum(self.model.params[key],self.model.grads[key],self.delta_x[key],self.init_lr)class Adam(Optimizer):def __init__(self, init_lr, model, beta1, beta2, epsilon):"""Adam优化器初始化输入:- init_lr:初始学习率- model:模型,model.params存储模型参数值- beta1, beta2:移动平均的衰减率- epsilon:保持数值稳定性而设置的常数"""super(Adam, self).__init__(init_lr=init_lr, model=model)self.beta1 = beta1self.beta2 = beta2self.epsilon = epsilonself.M, self.G = {}, {}for key in self.model.params.keys():self.M[key] = 0self.G[key] = 0self.t = 1def adam(self, x, gradient_x, G, M, t, init_lr):"""adam算法更新参数输入:- x:参数- G:梯度平方的加权移动平均- M:梯度的加权移动平均- t:迭代次数- init_lr:初始学习率"""M = self.beta1 * M + (1 - self.beta1) * gradient_xG = self.beta2 * G + (1 - self.beta2) * gradient_x ** 2M_hat = M / (1 - self.beta1 ** t)G_hat = G / (1 - self.beta2 ** t)t += 1x -= init_lr / torch.sqrt(G_hat + self.epsilon) * M_hatreturn x, G, M, tdef step(self):"""参数更新"""for key in self.model.params.keys():self.model.params[key], self.G[key], self.M[key], self.t = self.adam(self.model.params[key],self.model.grads[key],self.G[key],self.M[key],self.t,self.init_lr)class OptimizedFunction3D(Op):def __init__(self):super(OptimizedFunction3D, self).__init__()self.params = {'x': 0}self.grads = {'x': 0}def forward(self, x):self.params['x'] = xreturn x[0] * x[0] / 20 + x[1] * x[1] / 1 # x[0] ** 2 + x[1] ** 2 + x[1] ** 3 + x[0] * x[1]def backward(self):x = self.params['x']gradient1 = 2 * x[0] / 20gradient2 = 2 * x[1] / 1grad1 = torch.Tensor([gradient1])grad2 = torch.Tensor([gradient2])self.grads['x'] = torch.cat([grad1, grad2])class Visualization3D(animation.FuncAnimation):""" 绘制动态图像,可视化参数更新轨迹 """def __init__(self, *xy_values, z_values, labels=[], colors=[], fig, ax, interval=100, blit=True, **kwargs):"""初始化3d可视化类输入:xy_values:三维中x,y维度的值z_values:三维中z维度的值labels:每个参数更新轨迹的标签colors:每个轨迹的颜色interval:帧之间的延迟(以毫秒为单位)blit:是否优化绘图"""self.fig = figself.ax = axself.xy_values = xy_valuesself.z_values = z_valuesframes = max(xy_value.shape[0] for xy_value in xy_values)self.lines = [ax.plot([], [], [], label=label, color=color, lw=2)[0]for _, label, color in zip_longest(xy_values, labels, colors)]self.points = [ax.plot([], [], [], color=color, markeredgewidth=1, markeredgecolor='black', marker='o')[0]for _, color in zip_longest(xy_values, colors)]# print(self.lines)super(Visualization3D, self).__init__(fig, self.animate, init_func=self.init_animation, frames=frames,interval=interval, blit=blit, **kwargs)def init_animation(self):# 数值初始化for line in self.lines:line.set_data_3d([], [], [])# for point in self.points:# point.set_data_3d([], [], [])return self.linesdef animate(self, i):# 将x,y,z三个数据传入,绘制三维图像for line, xy_value, z_value in zip(self.lines, self.xy_values, self.z_values):line.set_data_3d(xy_value[:i, 0], xy_value[:i, 1], z_value[:i])# for point, xy_value, z_value in zip(self.points, self.xy_values, self.z_values):# point.set_data_3d(xy_value[i, 0], xy_value[i, 1], z_value[i])return self.linesdef train_f(model, optimizer, x_init, epoch):x = x_initall_x = []losses = []for i in range(epoch):all_x.append(copy.deepcopy(x.numpy())) # 浅拷贝 改为 深拷贝, 否则List的原值会被改变。 Edit by David 2022.12.4.loss = model(x)losses.append(loss)model.backward()optimizer.step()x = model.params['x']return torch.Tensor(np.array(all_x)), losses# 构建5个模型,分别配备不同的优化器
model1 = OptimizedFunction3D()
opt_gd = SimpleBatchGD(init_lr=0.95, model=model1)model2 = OptimizedFunction3D()
opt_adagrad = Adagrad(init_lr=1.5, model=model2, epsilon=1e-7)model3 = OptimizedFunction3D()
opt_rmsprop = RMSprop(init_lr=0.05, model=model3, beta=0.9, epsilon=1e-7)model4 = OptimizedFunction3D()
opt_momentum = Momentum(init_lr=0.1, model=model4, rho=0.9)model5 = OptimizedFunction3D()
opt_adam = Adam(init_lr=0.3, model=model5, beta1=0.9, beta2=0.99, epsilon=1e-7)models = [model1, model2, model3, model4, model5]
opts = [opt_gd, opt_adagrad, opt_rmsprop, opt_momentum, opt_adam]
# models = [model1]
# opts = [opt_gd]
x_all_opts = []
z_all_opts = []
#
# # 使用不同优化器训练
#
for model, opt in zip(models, opts):x_init = torch.FloatTensor([-7, 2])x_one_opt, z_one_opt = train_f(model, opt, x_init, 100) # epoch# 保存参数值x_all_opts.append(x_one_opt.numpy())z_all_opts.append(np.squeeze(z_one_opt))# 使用numpy.meshgrid生成x1,x2矩阵,矩阵的每一行为[-3, 3],以0.1为间隔的数值
x1 = np.arange(-10, 10, 0.01)
x2 = np.arange(-5, 5, 0.01)
x1, x2 = np.meshgrid(x1, x2)
init_x = torch.Tensor(np.array([x1, x2]))model = OptimizedFunction3D()# 绘制 f_3d函数 的 三维图像
fig = plt.figure()
ax = plt.axes(projection='3d')
X = init_x[0].numpy()
Y = init_x[1].numpy()
Z = model(init_x).numpy() # 改为 model(init_x).numpy() David 2022.12.4
surf = ax.plot_surface(X, Y, Z, edgecolor='grey', cmap=cm.coolwarm)
# fig.colorbar(surf, shrink=0.5, aspect=1)
# ax.set_zlim(-3, 2)
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel('f(x1,x2)')labels = ['SGD', 'AdaGrad', 'RMSprop', 'Momentum', 'Adam'] #
colors = ['#8B0000', '#0000FF', '#000000', '#008B00', '#FF0000'] #
#
animator = Visualization3D(*x_all_opts, z_values=z_all_opts, labels=labels, colors=colors, fig=fig, ax=ax)
ax.legend(loc='upper right')plt.show()
# animator.save('teaser' + '.gif', writer='imagemagick',fps=10) # 效果不好,估计被挡住了…… 有待进一步提高 Edit by David 2022.12.4
# save不好用,不费劲了,安装个软件做gif https://pc.qq.com/detail/13/detail_23913.html输出结果:

3.复现CS231经典动画
import torch
import numpy as np
import copy
from matplotlib import pyplot as plt
from matplotlib import animation
from itertools import zip_longest
from matplotlib import cmclass Op(object):def __init__(self):passdef __call__(self, inputs):return self.forward(inputs)# 输入:张量inputs# 输出:张量outputsdef forward(self, inputs):# return outputsraise NotImplementedError# 输入:最终输出对outputs的梯度outputs_grads# 输出:最终输出对inputs的梯度inputs_gradsdef backward(self, outputs_grads):# return inputs_gradsraise NotImplementedErrorclass Optimizer(object): # 优化器基类def __init__(self, init_lr, model):"""优化器类初始化"""# 初始化学习率,用于参数更新的计算self.init_lr = init_lr# 指定优化器需要优化的模型self.model = modeldef step(self):"""定义每次迭代如何更新参数"""passclass SimpleBatchGD(Optimizer):def __init__(self, init_lr, model):super(SimpleBatchGD, self).__init__(init_lr=init_lr, model=model)def step(self):# 参数更新if isinstance(self.model.params, dict):for key in self.model.params.keys():self.model.params[key] = self.model.params[key] - self.init_lr * self.model.grads[key]class Adagrad(Optimizer):def __init__(self, init_lr, model, epsilon):"""Adagrad 优化器初始化输入:- init_lr: 初始学习率 - model:模型,model.params存储模型参数值 - epsilon:保持数值稳定性而设置的非常小的常数"""super(Adagrad, self).__init__(init_lr=init_lr, model=model)self.G = {}for key in self.model.params.keys():self.G[key] = 0self.epsilon = epsilondef adagrad(self, x, gradient_x, G, init_lr):"""adagrad算法更新参数,G为参数梯度平方的累计值。"""G += gradient_x ** 2x -= init_lr / torch.sqrt(G + self.epsilon) * gradient_xreturn x, Gdef step(self):"""参数更新"""for key in self.model.params.keys():self.model.params[key], self.G[key] = self.adagrad(self.model.params[key],self.model.grads[key],self.G[key],self.init_lr)class RMSprop(Optimizer):def __init__(self, init_lr, model, beta, epsilon):"""RMSprop优化器初始化输入:- init_lr:初始学习率- model:模型,model.params存储模型参数值- beta:衰减率- epsilon:保持数值稳定性而设置的常数"""super(RMSprop, self).__init__(init_lr=init_lr, model=model)self.G = {}for key in self.model.params.keys():self.G[key] = 0self.beta = betaself.epsilon = epsilondef rmsprop(self, x, gradient_x, G, init_lr):"""rmsprop算法更新参数,G为迭代梯度平方的加权移动平均"""G = self.beta * G + (1 - self.beta) * gradient_x ** 2x -= init_lr / torch.sqrt(G + self.epsilon) * gradient_xreturn x, Gdef step(self):"""参数更新"""for key in self.model.params.keys():self.model.params[key], self.G[key] = self.rmsprop(self.model.params[key],self.model.grads[key],self.G[key],self.init_lr)class Momentum(Optimizer):def __init__(self, init_lr, model, rho):"""Momentum优化器初始化输入:- init_lr:初始学习率- model:模型,model.params存储模型参数值- rho:动量因子"""super(Momentum, self).__init__(init_lr=init_lr, model=model)self.delta_x = {}for key in self.model.params.keys():self.delta_x[key] = 0self.rho = rhodef momentum(self, x, gradient_x, delta_x, init_lr):"""momentum算法更新参数,delta_x为梯度的加权移动平均"""delta_x = self.rho * delta_x - init_lr * gradient_xx += delta_xreturn x, delta_xdef step(self):"""参数更新"""for key in self.model.params.keys():self.model.params[key], self.delta_x[key] = self.momentum(self.model.params[key],self.model.grads[key],self.delta_x[key],self.init_lr)
class Nesterov(Optimizer):def __init__(self, init_lr, model, rho):super(Nesterov, self).__init__(init_lr=init_lr, model=model)self.delta_x = {}for key in self.model.params.keys():self.delta_x[key] = 0self.rho = rhodef nesterov(self, x, gradient_x, delta_x, init_lr):"""Nesterov算法更新参数,delta_x为梯度的加权移动平均"""delta_x_prev = delta_xdelta_x = self.rho * delta_x - init_lr * gradient_xx += -self.rho * delta_x_prev + (1 + self.rho) * delta_xreturn x, delta_xdef step(self):"""参数更新"""for key in self.model.params.keys():self.model.params[key], self.delta_x[key] = self.nesterov(self.model.params[key],self.model.grads[key],self.delta_x[key],self.init_lr)class Adam(Optimizer):def __init__(self, init_lr, model, beta1, beta2, epsilon):"""Adam优化器初始化输入:- init_lr:初始学习率- model:模型,model.params存储模型参数值- beta1, beta2:移动平均的衰减率- epsilon:保持数值稳定性而设置的常数"""super(Adam, self).__init__(init_lr=init_lr, model=model)self.beta1 = beta1self.beta2 = beta2self.epsilon = epsilonself.M, self.G = {}, {}for key in self.model.params.keys():self.M[key] = 0self.G[key] = 0self.t = 1def adam(self, x, gradient_x, G, M, t, init_lr):"""adam算法更新参数输入:- x:参数- G:梯度平方的加权移动平均- M:梯度的加权移动平均- t:迭代次数- init_lr:初始学习率"""M = self.beta1 * M + (1 - self.beta1) * gradient_xG = self.beta2 * G + (1 - self.beta2) * gradient_x ** 2M_hat = M / (1 - self.beta1 ** t)G_hat = G / (1 - self.beta2 ** t)t += 1x -= init_lr / torch.sqrt(G_hat + self.epsilon) * M_hatreturn x, G, M, tdef step(self):"""参数更新"""for key in self.model.params.keys():self.model.params[key], self.G[key], self.M[key], self.t = self.adam(self.model.params[key],self.model.grads[key],self.G[key],self.M[key],self.t,self.init_lr)class OptimizedFunction3D(Op):def __init__(self):super(OptimizedFunction3D, self).__init__()self.params = {'x': 0}self.grads = {'x': 0}def forward(self, x):self.params['x'] = xreturn - x[0] * x[0] / 2 + x[1] * x[1] / 1 # x[0] ** 2 + x[1] ** 2 + x[1] ** 3 + x[0] * x[1]def backward(self):x = self.params['x']gradient1 = - 2 * x[0] / 2gradient2 = 2 * x[1] / 1grad1 = torch.Tensor([gradient1])grad2 = torch.Tensor([gradient2])self.grads['x'] = torch.cat([grad1, grad2])class Visualization3D(animation.FuncAnimation):""" 绘制动态图像,可视化参数更新轨迹 """def __init__(self, *xy_values, z_values, labels=[], colors=[], fig, ax, interval=100, blit=True, **kwargs):"""初始化3d可视化类输入:xy_values:三维中x,y维度的值z_values:三维中z维度的值labels:每个参数更新轨迹的标签colors:每个轨迹的颜色interval:帧之间的延迟(以毫秒为单位)blit:是否优化绘图"""self.fig = figself.ax = axself.xy_values = xy_valuesself.z_values = z_valuesframes = max(xy_value.shape[0] for xy_value in xy_values)# , marker = 'o'self.lines = [ax.plot([], [], [], label=label, color=color, lw=2)[0]for _, label, color in zip_longest(xy_values, labels, colors)]print(self.lines)super(Visualization3D, self).__init__(fig, self.animate, init_func=self.init_animation, frames=frames,interval=interval, blit=blit, **kwargs)def init_animation(self):# 数值初始化for line in self.lines:line.set_data([], [])# line.set_3d_properties(np.asarray([])) # 源程序中有这一行,加上会报错。 Edit by David 2022.12.4return self.linesdef animate(self, i):# 将x,y,z三个数据传入,绘制三维图像for line, xy_value, z_value in zip(self.lines, self.xy_values, self.z_values):line.set_data(xy_value[:i, 0], xy_value[:i, 1])line.set_3d_properties(z_value[:i])return self.linesdef train_f(model, optimizer, x_init, epoch):x = x_initall_x = []losses = []for i in range(epoch):all_x.append(copy.deepcopy(x.numpy())) # 浅拷贝 改为 深拷贝, 否则List的原值会被改变。 Edit by David 2022.12.4.loss = model(x)losses.append(loss)model.backward()optimizer.step()x = model.params['x']return torch.Tensor(np.array(all_x)), losses# 构建5个模型,分别配备不同的优化器
model1 = OptimizedFunction3D()
opt_gd = SimpleBatchGD(init_lr=0.05, model=model1)model2 = OptimizedFunction3D()
opt_adagrad = Adagrad(init_lr=0.05, model=model2, epsilon=1e-7)model3 = OptimizedFunction3D()
opt_rmsprop = RMSprop(init_lr=0.05, model=model3, beta=0.9, epsilon=1e-7)model4 = OptimizedFunction3D()
opt_momentum = Momentum(init_lr=0.05, model=model4, rho=0.9)model5 = OptimizedFunction3D()
opt_adam = Adam(init_lr=0.05, model=model5, beta1=0.9, beta2=0.99, epsilon=1e-7)model6 = OptimizedFunction3D()
opt_nesterov = Nesterov(init_lr=0.01, model=model6, rho=0.9)models = [model5, model2, model3, model4, model1]
opts = [opt_adam, opt_adagrad, opt_rmsprop, opt_momentum, opt_gd]x_all_opts = []
z_all_opts = []# 使用不同优化器训练for model, opt in zip(models, opts):x_init = torch.FloatTensor([0.00001, 0.5])x_one_opt, z_one_opt = train_f(model, opt, x_init, 500) # epoch# 保存参数值x_all_opts.append(x_one_opt.numpy())z_all_opts.append(np.squeeze(z_one_opt))# 使用numpy.meshgrid生成x1,x2矩阵,矩阵的每一行为[-3, 3],以0.1为间隔的数值
x1 = np.arange(-1, 2, 0.01)
x2 = np.arange(-1, 1, 0.05)
x1, x2 = np.meshgrid(x1, x2)
init_x = torch.Tensor(np.array([x1, x2]))model = OptimizedFunction3D()# 绘制 f_3d函数 的 三维图像
fig = plt.figure()
ax = plt.axes(projection='3d')
X = init_x[0].numpy()
Y = init_x[1].numpy()
Z = model(init_x).numpy() # 改为 model(init_x).numpy() David 2022.12.4
surf = ax.plot_surface(X, Y, Z, edgecolor='grey', cmap=cm.coolwarm)
# fig.colorbar(surf, shrink=0.5, aspect=1)
ax.set_zlim(-3, 2)
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel('f(x1,x2)')labels = ['Adam', 'AdaGrad', 'RMSprop', 'Momentum', 'SGD']
colors = ['#8B0000', '#0000FF', '#000000', '#008B00', '#FF0000']animator = Visualization3D(*x_all_opts, z_values=z_all_opts, labels=labels, colors=colors, fig=fig, ax=ax)
ax.legend(loc='upper right')plt.show()
# animator.save('animation.gif') # 效果不好,估计被挡住了…… 有待进一步提高 Edit by David 2022.12.4输出结果如下:

首先解决老师上课提出的疑问,SGN处于鞍点怎么摆脱的问题,其实老师给的代码已经嘎嘎完美了,最开始我通过打印SGD的梯度观察随着迭代梯度到底是否为0了,如果为0则说明,肯定是卡在鞍点了,但是我打完的结果如下,取其中的一小部分

修改方式如下:
class SimpleBatchGD(Optimizer):def __init__(self, init_lr, model):super(SimpleBatchGD, self).__init__(init_lr=init_lr, model=model)self.i = 1def step(self):# 参数更新if isinstance(self.model.params, dict):for key in self.model.params.keys():self.model.params[key] = self.model.params[key] - self.init_lr * self.model.grads[key]print('第'+str(self.i)+'次更新的梯度为:', torch.round(self.model.params[key], decimals=4))self.i = self.i + 1因为更细的梯度很小并且这个时候的学习率 * 梯度就导致更新的更小,但是并不是完全陷入鞍点“无法自拔”,所以在我将epoches提升到500的时候我发现SGD就成功逃离鞍点了。如上图的输出结果一致。但是在显示Nesterov的时候我们发现SGD突然没咯,经过不断验证我发现,Nesterov是覆盖了SGD的路径,简单的说就是两个路径大致相似,只能显示一个出来。

代码如下(只需修改四个位置,可通过ctrl+F在之前代码的基础上,搜索进行修改) :
models = [model5, model2, model3, model4, model1, model6]
opts = [opt_adam, opt_adagrad, opt_rmsprop, opt_momentum, opt_gd, opt_nesterov]# ...
# ...
# ...labels = ['Adam', 'AdaGrad', 'RMSprop', 'Momentum', 'SGD', 'Nesterov']
colors = ['#8B0000', '#0000FF', '#000000', '#008B00', '#FF0000', '#F36D7D']4.结合3D动画,用自己的语言,从轨迹、速度等多个角度讲解各个算法优缺点
- SGD
- 轨迹:SGD沿着负梯度方向更新参数,因此在二维空间中表现为z字抖动的直线状的下降轨迹。
- 速度:由于每次更新只考虑当前样本的梯度信息,SGD可能会出现参数更新的抖动现象,导致收敛速度较慢。并且根据3D图我们发现,SGD很容易在鞍点的位置更新缓慢,不利于逃离鞍点。
- AdaGrad
- 轨迹:Adagrad根据参数的历史梯度信息来自适应地调整学习率。所以在二维空间中表现为曲线轨迹且越来越密的下降轨迹。
- 速度:在优化过程中,学习率可能会逐渐减小,导致参数更新幅度逐渐减小。适应性学习率的设计可以加快收敛速度,但在长时间训练中,可能会导致学习率过小,反而降低收敛速度。在3D图中我们可以明显 发现AdaGrad的速度与Adam等算法都是齐头并进的高速算法,但是最后却被一个又一个算法超越。假设时间无限长,我相信AdaGrad估计会是最后最慢的算法。
- RMSprop
- 轨迹:RMSprop通过对梯度的平方进行指数加权移动平均来调整学习率。所以在二位空间中表现为曲线轨迹且线上的点分布较为平均的下降轨迹。
- 速度:指数加权移动平均的设计使得它能够在优化过程中动态地调整学习率,并可能产生适应性学习率的调整。可在有些情况下避免 AdaGrad中学习率不断单调下降,防止过早衰减,速度在我看来是最快,最稳定的优化算法(在cs231复现的实验环境下)
- Momentum
- 轨迹:动量算法引入了动量项,它考虑了参数更新时的历史梯度信息。但是因为历史梯度信息会出现物理上说的惯性现象,对于更新来有好有坏,能逃离局部最优点,但是会因为惯性,走了很多歪路,但是大大减少了SGD算法的反复z字抖动的情况,在二维空间中表现为,靠近局部最优点,点的轨迹分布较为集中,原理分布较为松散
- 速度:通过对轨迹的描述,我们明确发现在局部最优点附近的,点的更新较小,速度慢,原理局部最优点的地方速度较快
- Adam
- 轨迹:这个轨迹不太好描述,因为Adam 约等于 动量法 + RMSprop,所以同时具有两个算法的有点,路径较为平稳,并且能很好的躲避局部最优点,不像动量法靠惯性原则一点点躲避局部最优点,而在开始就是逃离。
- 速度:cs231的环境下,Adam具有今次RMSprop的速度,一位内Adam是对RMSprop+动量法的优化,但是,在逃离局部最优点后,动量法的惯性原则,会让Adam成曲线运动,而非RMSprop的类直线运动,降低速度。
- Nesterov
- 轨迹:类似动量法,Nesterov是动量法的优化,在cs231的环境下,轨迹与动量法大致相同
- 速度:速度是让我最奇怪的,因为动量法是Nesterov的基础班,但是无论是逃离局部最优点,还是逃离后的收敛速度,我感觉都不如动量法,嗯....,分析了好半天我也没太太想明白,等期末结束再来想想吧~存个疑
5.总结
一说优化算法,就让我先想了让我当时一阵头疼的最优化方法,当时学的都是牛顿法、黄金分割啥的,现在很少用。这节课学的这些当下较为流行的优化算法,说实话,真不如最优化方法中的数学理论难,奔着学就学明白,不断研究每个算法的特点,总结出自己的一套选择规则,应该就是这节课的意义。