1 简介
来自源的信号通常处于时域。例如正弦信号、生物医学信号等。任何时域信号都可以使用数学变换进行处理或变换到频域(谱域)。傅里叶变换是一种流行或著名的变换,它将时域信号转换为频域信号,而不失一般性。
在绘制时域信号时,在 x 轴上使用时间,在 y 轴上使用幅度。信号中存在的隐藏信息无法在时域中揭示,因此需要变换域。信号的频谱就是信号的频率内容(频谱分量)。信号的频谱描述了信号中存在的所有频率。绘制频域时,在 x 轴上使用频率,在 y 轴上使用幅度。
通常对于任何信号,如果频率成分不随时间变化,则称为平稳信号。例如正弦信号,其中频率“X”Hz 不改变,与周期无关。不幸的是,实时信号是非平稳信号,信号的频率内容不断变化。最好的例子是生物信号。假设我们正在查看 ECG(心电图)信号。心脏病专家熟知健康心电图信号的典型形状。任何与该形状的显着偏差通常被认为是病理状况的症状。医生不仅在时域中分析这些病例,他们还使用频域来确认病理状况。
2 傅立叶变换
关于频率内容或频谱的第一个也是主要的贡献来自法国数学家约翰·巴普蒂斯·傅立叶。他证明任何周期函数都可以表示为周期复指数函数的无限和,并命名为傅里叶变换(FT)。
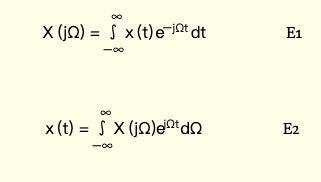
x ( t ) x(t) x(t) 表示时域信息, X ( j Ω ) X(j\Omega) X(jΩ) 表示信号的频率内容,其中 Ω = 2 × π × F \Omega=2 \times \pi \times F Ω=2×π×F,
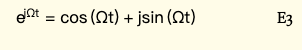
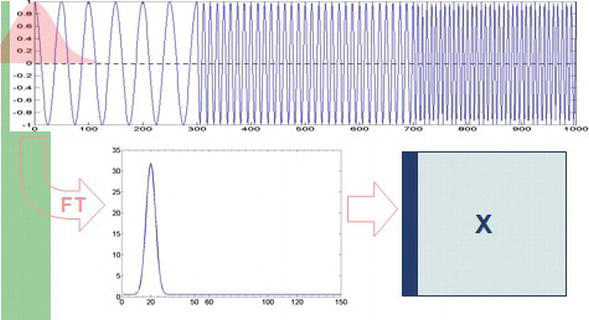
式1的输入信号在时间维度上与三角函数相成并相加(积分)得到频率内容。可通过下图理解:
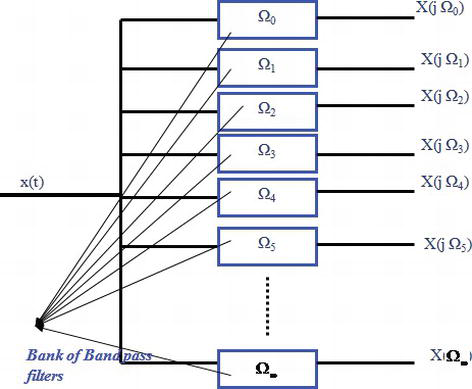
上图展示了时间域到频率域:图中蓝色部分表示窄波段过滤(去除部分频率)。
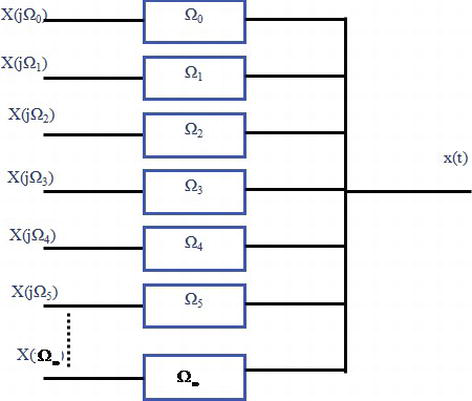
上图展示了频率域到时间域:图中蓝色部分表示窄波段过滤(去除部分频率)。
3 短时傅里叶变换

上式表明输入信号 x(t) 通过持续时间为“ τ \tau τ”的窗口进行斩波,并进行傅里叶变换。换句话说,假设信号在间隔“ τ \tau τ”内是静止的。在信号的整个持续时间内重复此过程。现在,傅里叶变换面临的问题在某种程度上得到了解决,得到了指定窗口持续时间的频率分量。
下图显示了如何针对窗口的一步的非平稳信号采用 STFT:
现在,窗口宽度的选择在STFT中起着至关重要的作用。我们选择的窄窗口会导致频率分辨率较差而时间分辨率良好,如下图所示。

如果选择较宽的窗口,则会出现相反的效果,如下图所示:
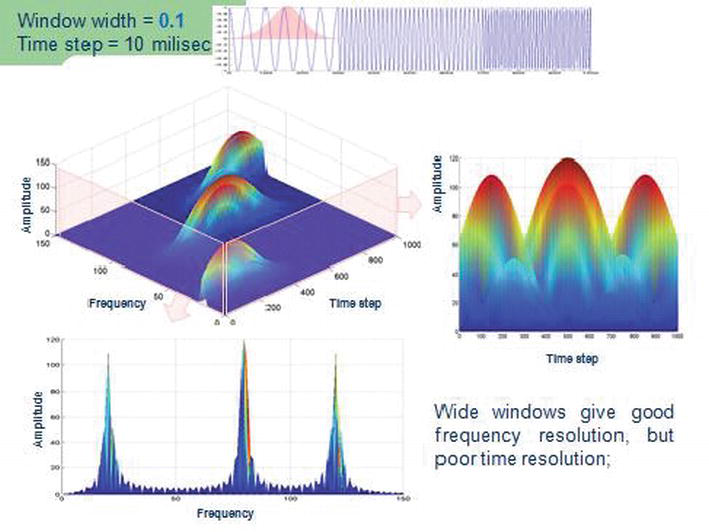
STFT为傅里叶变换所面临的问题提供解决方案,但缺点是所使用的窗口宽度是恒定的,因此它仅提供固定的分辨率。
通常,信号可以携带低频和高频分量。为了捕获两者,需要不同宽度的窗口,而 STFT 没有提供这一点。为了更清楚地理解,STFT 中不存在多分辨率的概念。因此,需要一个新的转换来解决上述问题。解决方案是小波变换。
4 连续小波变换
小波变换背后的基本思想是,引入一种新的基(窗口)函数,可以放大或压缩该函数以捕获信号的低频和高频分量(与尺度有关)。方程如下:
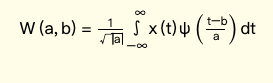
W ( a , b ) W(a,b) W(a,b)表示小波系数, a a a 表示尺度参数, b b b 表示偏移参数。 ψ ( t ) \psi(t) ψ(t)称为母小波。不同的膨胀和平移导致不同的子小波。
任何原始数据或信号都可以用小波展开来表示。使用小波对数据的最佳表示取决于选择的最佳或接近的小波。根据文献,有许多可用的小波。 Haar 和 Daubechies 是小波的一些例子;基于高斯的小波,有Mexican hat小波和Morlet小波;在基于多项式的小波下,有Battle-lemarie、Coiflet和基于Spline的小波;在Sinc小波下,有Meyer小波和Shannon小波。
5 离散小波变换
从前面的理解可以看出,CWT是一种冗余变换,这意味着平移参数“b”和缩放参数“a”似乎是无限的,这使得它们在实现方面变得困难。 CWT 似乎总是可计算但不可实现。
小波变换的实现解决方案源自离散小波变换(DWT)。 DWT 中在二元(八度)网格上的时频平面进行采样,这使得它们在实现方面非常高效。缩放参数“a”被 2 − j 2^{−j} 2−j 替换,“b”与“a”成比例,即 b = k 2 − j b = k 2^{−j} b=k2−j 。这里 ‘j’被称为缩放参数,‘k’是比例常数,在DWT中起移位参数的作用。
将 a = 2 − j , b = k 2 − j a=2^{−j},b = k 2^{−j} a=2−j,b=k2−j(j和k为整数)代入上式,得到方程:
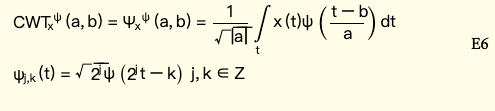
再转到时域:
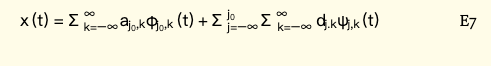
6 结论
不同数量的小波具有不同的信号处理特性,例如紧支撑、对称性、规律性和消失矩,因此它们适用于信号去噪、检测信号中的不连续性和击穿点、压缩图像、识别纯频率等领域、地震和地球物理信号处理、视频压缩、声学数据分析、核工程、神经生理学、音乐、磁共振成像、语音识别、光学、分形、湍流、地震预测、雷达、人类视觉等。
参考:https://www.intechopen.com/chapters/61705
![web:[BJDCTF2020]The mystery of ip(ssti模板注入、Smarty 模板引擎)](https://img-blog.csdnimg.cn/direct/f6884aa9d28b4722a2c0cca18ce80514.png)