动力学约束下的运动规划算法——Kinodynamic RRT*算法-编程知识

一、RRT * 算法回顾

为了更好的理解Kinodynamic RRT*算法，我们先来回顾一下RRT * 算法

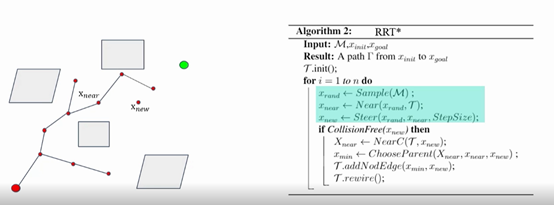
RRT * 先通过Sample函数随机选取一个点Xrand，然后通过Near函数找到当前树上距离Xrand最近的一个点Xnear，再通过Steer函数，沿着从Xnear到Xrand的方向走一步，步长为Stepsize，得到一个点Xnew

与RRT不同的是，在得到Xnew后不是直接将Xnew与Xnear连起来，而是通过NearC函数在以Xnew为圆心的，R为半径的圆的区域内去找到Xnew附近的一些节点，如上图中的Xnear、X1、X2

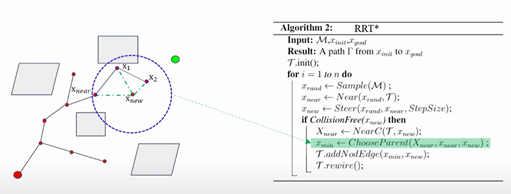
然后通过ChooseParent函数，将Xnew将这些点连接起来，分别计算从起点到Xnew的这三条路径哪一个花费是比较小的，这里的花费可以选为路径最短，也可以选择其他标准，上图中的例子中通过Xnear到达Xnew的那条路是最短的，这个时候Xnear就被选作了Xnew的父节点，如下图所示

然后通过rewire函数去优化路径，将X1和X2分别与Xnew相连，去判断原来从起始点到X1的路更好，还是现在经过Xnew到X1的路更好，这里采用的衡量标准是路径长度，显然对于X1而言，是原来的路更短，不做处理，对于X2而言，显然是经过Xnew的路更短，因此将X2的父节点更改为Xnew，如下图所示：

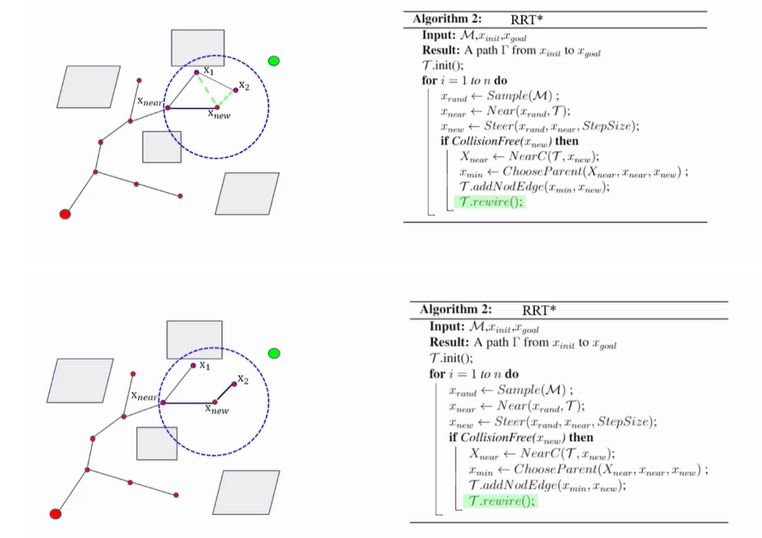
除此之外，相对于RRT算法，RRT*在找到一条从起点到终点的路径后并没有停止，而是不断的优化，所以说RRT * 是一种渐进最优的算法，而RRT是一种非最优的算法

二、Kinodynamic RRT*算法

基于上面对RRT * 算法的回顾，接下来我们来看一下Kinodynamic RRT * 算法与传统的RRT * 算法有哪些不同

在这里插入图片描述

1、采样——Sample

传统的RRT * 算法在采样时在欧几里德空间中仅对位置进行采样，而Kinodynamic RRT * 算法是在全状态空间中采样。比如，针对位置、速度进行采样。

在这里插入图片描述

2、寻找RRT树上最"邻近"节点——Near

与传统的RRT * 算法不同，Kinodynamic RRT*算法在寻找最"邻近"节点时，不能仅考虑位置上最接近，而是需要考虑动力学约束，所以个人认为这里的最“邻近”节点，可以理解成到新节点连接代价值最小的节点。

在这里插入图片描述

上述过程中需要求解两个节点间的轨迹，即两点边界值问题BVP、或最优两点边界值问题OBVP。该问题可以通过前文介绍的庞特里亚金最小值原理进行求解，链接如下：

动力学约束下的运动规划算法——两点边界值最优控制问题 OBVP

提出Kinodynamic RRT*算法的作者在论文中给出了另一种求解该问题的方法，下面对该方法进行介绍。若不关心该方法，可略过该部分，直接跳到第3条

如果引入最优控制，我们可以定义如下的状态转移代价函数(通常采用二次型的时间-能量最优，即希望能量花费最小，并且耗费的时间要尽可能的小)
$c[\pi]=\int_0^\tau\left(1+u(t)^TRu(t)\right)dt$

如果从一种状态转移到另一种状态的成本很小，那么两种状态就很接近。(注意，如果反向转移，费用可能不同)

如果已知转移的到达时间τ和转移的控制策略u(t)，就可以计算出转移的成本，这是经典的最优控制解(OBVP)

（1）情况1：固定的最终状态x1，固定的最终时间τ

此时，最优控制策略 $u^{*}(t)$ 如下所示：

$u^*(t)=R^{-1}B^T\exp[A^T(\tau-t)]G(\tau)^{-1}[x_1-\bar{x}(\tau)].$
其中，𝐺𝑡为加权可控性Gramian,其表达式如下：

$G(t)=\int_0^t\exp[A(t-t^{\prime})]BR^{-1}B^T\exp[A^T(t-t^{\prime})]dt^{\prime}.$

上式即下面的李雅普诺夫方程的解

$\dot{G}(t)=AG(t)+G(t)A^T+BR^{-1}B^T,G(0)=0.$

最优控制策略 $u^{*}(t)$ 的表达式中的 $\bar{x}(t)$ 表示t时刻没有控制输入的状态x，其表达式如下：

$\bar{x}(t)=\exp(At)x_0+\int_0^t\exp[A(t-t^{\prime})]cdt^{\prime}.$
上式也就是下面微分方程的解

$\dot{\bar{x}}(t)=A\bar{x}(t)+c,\bar{x}(0)=x_0$

（2）情况2：固定的最终状态x1，自由的最终时间τ

如果我们想要找到最优到达时间τ，我们通过将控制策略 $u^{*}(t)$ 填充到代价函数 $c[\pi]$ 中，并计算积分来实现:

$c[\tau]=\tau+[x_1-\bar{x}(\tau)]^TG(t)^{-1}[x_1-\bar{x}(\tau)].$

通过 $c[\pi]$ 对τ求导可以得到最优τ:

$\dot{c}[\tau]=1-2(Ax_1+c)^Td(\tau)-d(\tau)^TBR^{-1}B^Td(\tau).$
其中

$d(\tau)=G(t)^{-1}[x_1-\bar{x}(\tau)].$

我们求解 $\dot{c}[\tau]$ =0，来得到最优的时间τ*，注意函数 $\dot{c}[\tau]$ 可能有多个局部极小值。对于二重积分器系统，它是一个四阶多项式。

得到最优的时间τ*后，给定最佳到达时间𝜏∗，它再次变成一个固定的最终状态，固定的最终时间问题，利用（1）中情况1介绍的方式求解即可。

3、选择父节点——ChooseParent

传统的RRT * 会计算所有以新节点为圆心的圆形区域内 RRT树上已有节点到新节点的代价值，并选取从起点到新节点总代价值最小的那条路线对应的节点作为父节点，这里的代价值一般指欧氏距离。

而在Kinodynamic RRT*算法中，是在高维空间中进行的，查找从该节点到达新节点所花费的代价成本u(t)在设定的范围内的RRT树上已有节点（状态点）,其区域是一个抽象的球形区域。

在这里插入图片描述

上述问题涉及到一个如何高效的查找近节点

如果每次我们对一个随机状态𝒙_𝒓𝒂𝒏𝒅进行采样时，都通过检查RRT树中的每个节点来找到它的父节点，这就是为每个节点求解OBVP，会耗费大量的时间和算力

如果我们设置一个允许的代价值上限𝒓，我们实际上可以计算出𝒙_𝒓𝒂𝒏𝒅可以到达的状态的边界(前向可达集)和以小于𝒓代价到达的状态的边界(反向可达集)。如果我们以kd-tree的形式存储节点，我们就可以在树中进行范围查询。

这里需要介绍这两个可达集合的概念，对于一个节点，在设定的最大代价成本𝒓内，可以到达的所有状态点的集合，称为该节点的前向可达解。同样，空间中所有可以以小于等于最大代价成本𝒓的代价到达该节点的状态点的集合，称为该节点的反向可达解。

前向可达解和反向可达解都有比较完备的算法进行计算，下面的公式描述了从状态𝒙𝟎转移到𝒙𝟏的成本随到达时间𝝉的变化。

$c[\tau]=\tau+[x_1-\bar{x}(\tau)]^TG(t)^{-1}[x_1-\bar{x}(\tau)].$

可以看出，给定初始状态𝒙𝟎，成本容差𝒓，到达时间𝝉，𝒙𝟎的前向可得集合(forward-reachable)为:

$\begin{gathered} \{x_1|\tau+[x_1-\bar{x}(\tau)]^TG(t)^{-1}[x_1-\bar{x}(\tau)]<r\} \\ =\left\{x_1\mid[x_1-\bar{x}(\tau)]^T\frac{G(t)^{-1}}{r-\tau}[x_1-\bar{x}(\tau)]<1\right\}. \\ =\mathcal{E}[\bar{x}(\tau),G(t)(r-\tau)]. \end{gathered}$

其中, $\mathcal{E}[x,M]$ 是以x为中心的椭球，𝑀为正定矩阵， $\mathcal{E}[x,M]$ 的表达式如下：

$\mathcal{E}[x,M]=\{x^{\prime}\mid(x^{\prime}-x)^TM^{-1}(x^{\prime}-x){<}1\}.$

因此，前向可达集是所有可能到达时间𝝉的高维椭球的并集,如下图所示：

在这里插入图片描述

为了简化，我们选取几个𝝉，计算每个𝝉的椭球的轴向包围盒，并更新每个维度的最大值和最小值:

$\prod_{k=1}^n\begin{bmatrix}min\{0<\tau<r\}\big(\bar{x}(\tau)_k-\sqrt{G[\tau]_{(k,k)}(r-\tau)}\big),\\max\{0<\tau<r\}\big(\bar{x}(\tau)_k+\sqrt{G[\tau]_{(k,k)}(r-\tau)}\big)\end{bmatrix}.$