机器学习作业--PCA-编程知识

机器学习作业--PCA

特征约减：

为什么进行特征约减？

怎么获得更具有代表性的数据？

怎么找到主成分，满足上述条件？

代码：

学习资料：PCA算法 - 知乎 (zhihu.com)

特征约减：

将高维的特征向量X转化成Y： $X^{p}\rightarrow Y^{d}$ ， $(d<<p)$

其中： $G^{d\times p}\epsilon R$ ， $X^{p}\epsilon R$

通过G与X做矩阵乘法进行维度转换： $G\times X=Y^{d}$

为什么进行特征约减？

1.有价值的特征信息少；

2.维度太大，查询检索的工作量大。

特征约减将p维的数据集转换为d维的数据集，但是降维时我们会损失部分数据，我们希望损失降低较小，保留更具有代表性的数据。

介绍常见的一种维度约减方法--PCA

怎么获得更具有代表性的数据？

下图中：蓝色点表示数据点集，每个数据表示为（x1,x2）。现在我们需要将二维数据集降成一维即，把二维散点转化为下图中红线上的点。（二维数据集为X,红线上点为Y,）那么红线1的代表性好还是红线2好？

思考：

如果将下面的点都映射到y轴上，下图中经过y=-2的点将会重合，损失了x坐标的信息；因此我们希望不同的点映射之后的位置不同，尽量不出现信息损失。

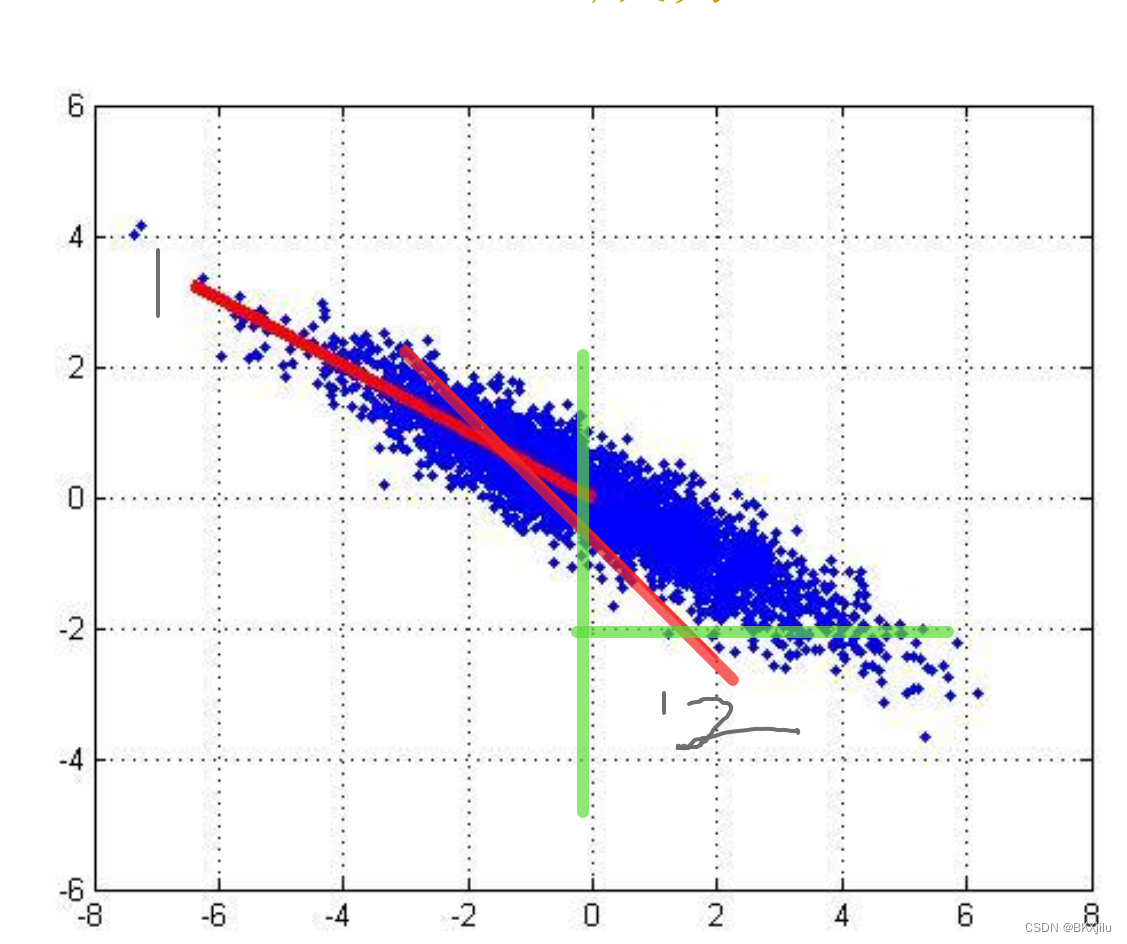
红线1的效果好：样本点在这个直线上的投影的离散程度更高。（通常把这个向量称为主成分）

希望数据投影的方差最大，方差越大，样本点在这个直线上的投影离散程度越高，效果越好。

怎么找到主成分，满足上述条件？

公式推导：

首先：给定n个样本，每个样本的维度为p维

${X_{1,},X_{2},...,Xn}\epsilon R^{p}$

定义 $Z_{1j}$ 为样本 $X_{j}$ 在主成分 $a_{1}$ 上的投影：

$Z_{1j}$ $=a_{1}^{\Gamma }X_{j}$

我们的目的是找到 $a_{1}$ ，使 $Z_{1j}$ 的方差最大

和前面的特征约减对应：

$G\leftarrow [a_{1},a_{2},...,a_{d}]$

$X_{j}\epsilon R^{p} \rightarrow G^{\Gamma }X_{j}\epsilon R^{d}$

$Z_{1j}$ 的方差：

$var[Z_{1j}]=\frac{1}{n}\sum_{i=1}^{n}(a_{1}^{\Gamma }x_{j}-a_{1}^{\Gamma }\overline{x})^{2}$

$=\frac{1}{n}\sum_{i=1}^{n}a_{1}^{\Gamma }(x_{i}-\overline{x})(x_{i}-\overline{x})^{\Gamma }a_{1}$

令： $S=\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\overline{x})(x_{i}-\overline{x})^{\Gamma }$

$var[Z_{1j}]=a_{1}^{\Gamma }Sa_{1}$

目标;找到主方向 $a_{1}$ ,使得 $var[Z_{1j}]=a_{1}^{\Gamma }Sa_{1}$ 最大，且 $a_{1}^{\Gamma }a_{1}=1$ （为什么满足这个条件，不太理解）

引入拉格朗日乘子：

$L=a_{1}^{\Gamma }Sa_{1}-\lambda (a_{1}^{\Gamma }a_{1}-1)$

$\frac{\varphi L}{\varphi a_{1}}=2Sa_{1}-2\lambda a_{1}=0$

$\Rightarrow Sa_{1}=\lambda a_{1}$

得出 a 1 是协方差矩阵 S 的特征向量。

数据集：人脸识别数据集

代码：

PCA算法流程：

1.计算数据集均值；

2.计算协方差

3.计算协方差的特征向量

4.选择d个特征向量。 $G\leftarrow [a_{1},a_{2},...,a_{d}]$ $X_{j}\epsilon R^{p} \rightarrow G^{\Gamma }X_{j}\epsilon R^{d}$

def pca(data,k):#计算均值mean = np.mean(data,axis=0)#xi-均值removed_mean = data-mean#协方差矩阵SS=np.cov(removed_mean)#计算特征值，特征向量feature_val,feature_vector = np.linalg.eig(np.mat(S)) #获取排列的索引val_idx = np.argsort(feature_val)#获取协方差最大的K个特征值和对应的特征向量val_idx = val_idx[:-(k + 1):-1]vects = feature_vector[:, val_idx]#GX->Ylow_dim = vects.T*removed_meanreturn low_dim,mean,vects

Sklearn:

import numpy as np
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.datasets import fetch_lfw_people# 加载LFW (Labeled Faces in the Wild) 人脸数据集
lfw_people = fetch_lfw_people(min_faces_per_person=70, resize=0.4)# 准备数据
X = lfw_people.data
y = lfw_people.target# 标准化数据
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.25, random_state=42)# 使用PCA进行特征降维
n_components = 150  # 选择要保留的主成分数量
pca = PCA(n_components=n_components, whiten=True, svd_solver='randomized')
pca.fit(X_train)# 将训练和测试数据转换到选定数量的主成分空间
X_train_pca = pca.transform(X_train)
X_test_pca = pca.transform(X_test)# 训练一个分类器（这里使用支持向量机作为示例）
clf = SVC(kernel='rbf', class_weight='balanced')
clf.fit(X_train_pca, y_train)# 在测试集上评估分类器
accuracy = clf.score(X_test_pca, y_test)
print("Accuracy: {:.2f}".format(accuracy))

总结：

特征约减的优点：