已知有限长序列：xk=1,2,1,1,0,-3, hk=[1,-1,1]

,

计算离散卷积和yk=xk*h(k) 。

程序如下：

function [t,x] = My_conv(x1,x2,t1,t2,dt)
%文件名与函数名对应
%自写的卷积函数
x = conv(x1,x2)*dt;
t0 = t1(1) + t2(1);
L = length(x1) + length(x2)-2;
t = t0:dt:(t0+L*dt);
end

clear;
k1 = [0, 1, 2, 3, 4, 5];   %xk的序列号
xk = [1, 2, 1, 1, 0, -3];   %xk的序列值
subplot(311);
stem(k1,xk,'filled');
title('x(k) = [1,2,1,1,0,-3]');
k2 = [0, 1, 2];
hk = [1, -1, 1];
subplot(312);
stem(k2, hk,'filled');
title('h(k) = [1,-1,1]');
[k3,yk] = My_conv(xk, hk, k1, k2, 1);   %调用卷积的函数
subplot(313);
stem(k3,yk,'filled');
title('y(k) 卷积后图像');

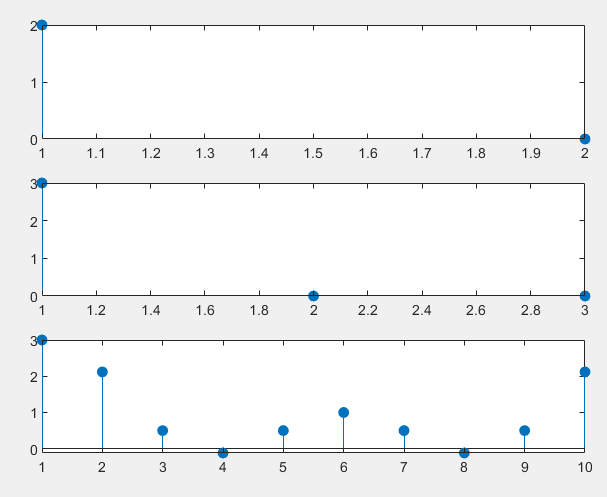
运行结果如下：

用MATLAB实现对信号xt=cos⁡(2π×20t) 的抽样。

代码如下：

clear;
Signal_Frequency = 20;    %信号频率
Signal_Ts = 0.001; %信号的采样间隔
t = 0 : Signal_Ts : 0.1;% fs = 10fc
Sample_Frequency = 1 * Signal_Frequency; %采样频率
Sample_Ts = 1 / Sample_Frequency;%抽样的间隔
xt = cos(2*pi * Signal_Frequency * t);
n = 0 : Sample_Ts : 0.1;
xn = cos(2*pi * Signal_Frequency * n);subplot(321); plot(t,xt); hold on;
stem(n,xn); title('fs = fc');
X1k = fft(xn, Sample_Frequency);
subplot(322); stem(X1k);% fs = 2fc
Sample_Frequency = 2 * Signal_Frequency; %采样频率
Sample_Ts = 1 / Sample_Frequency;%抽样的间隔
xt = cos(2*pi * Signal_Frequency * t);
n = 0 : Sample_Ts : 0.1;
xn = cos(2*pi * Signal_Frequency * n);
subplot(323); plot(t,xt); hold on;
stem(n,xn); title('fs = 2fc');
X10k = fft(xn, Sample_Frequency);
subplot(324); stem(X10k); title('fs = 2fc频谱');% fs = 10fc
Sample_Frequency = 10 * Signal_Frequency; %采样频率
Sample_Ts = 1 / Sample_Frequency;%抽样的间隔
xt = cos(2*pi * Signal_Frequency * t);
n = 0 : Sample_Ts : 0.1;
xn = cos(2*pi * Signal_Frequency * n);
subplot(325); plot(t,xt); hold on;
stem(n,xn); title('fs = 10fc')
X10k = fft(xn, Sample_Frequency);
subplot(326); stem(X10k); title('fs = 10fc频谱');

运行结果如下：

已知序列[xk]={1,1,1} ，对其频谱X(ejΩ) 进行抽样，分别取N=2,3,10观察频域抽样造成的混叠现象。

代码如下：

clear;
xn = [1, 1, 1];X2k = fft(xn,2);
subplot(311);
stem(X2k,'filled');X3k = fft(xn,3);
subplot(312);
stem(X3k,'filled');X10k = fft(xn, 10);
subplot(313);
stem(X10k,'filled');

运行结果如下：