1.离散化

     离散化是一个很好用的技巧，可以很大程度上降低时间和空间复杂度

     离散化是把无限空间中有限的个体映射到有限的空间中去，减少空间的使用。

     比如：我们有一组很大的数据 ：1  3  277438  2884821   428   239823128

     如果我们想要把这些数作为数组的下标来存储的话，我们就要开辟一个很大空间的数组，但很显然，其中很多空间我们是用不到的，浪费的不是一星半点，我接受不了，题目也不会让你过。

     总的来说，离散化的特点是这样的：

1.数据值域很大，但数据个数比较少，一般来说值域<=10^5，可以用前缀和，大于这个点就要考虑离散化
2.把值域里的数映射到连续的自然数的序列中，这个映射就是把数组的值映射到对应的下标

     但也存在着一些问题，比如：

1.数组存储值域的数可能有重复的元素，需要去重
2.怎么快速去映射，我们可以通过二分来快速算出x离散化后的值，即x对应的下标

  模板   

     让我们看看是如何实现的，下面给出模板：

vector<int> alls; // 存储所有待离散化的值
sort(alls.begin(), alls.end()); // 将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end());   // 去掉重复元素// 二分求出x对应的离散化的值
int find(int x) // 找到第一个大于等于x的位置
{int l = 0, r = alls.size() - 1;while (l +1!= r){int mid = l + r >> 1;if (alls[mid] >= x) r = mid;else l = mid ;}return r + 1; // 映射到1, 2, ...n
}

应用

    

#include <iostream>
#include <vector>
#include <algorithm>using namespace std;
const int N = 300010; 
int n, m;
int a[N];//存储坐标插入的值
int s[N];//存储数组a的前缀和
vector<int> alls;  //存储（所有与插入和查询有关的）坐标
vector<pair<int, int>> add, query; //存储插入和询问操作的数据int find(int x) { //返回的是输入的坐标的离散化下标int l = 0, r = alls.size() - 1;while (l+1!=r) {int mid = l + r >> 1;if (alls[mid] >= x) r = mid;else l = mid ;}return r + 1;
}int main() {scanf("%d%d", &n, &m);for (int i = 1; i <= n; i++) {int x, c;scanf("%d%d", &x, &c);add.push_back({x, c});alls.push_back(x);}for (int i = 1; i <= m; i++) {int l , r;scanf("%d%d", &l, &r);query.push_back({l, r});alls.push_back(l);alls.push_back(r);}//排序，去重sort(alls.begin(), alls.end());alls.erase(unique(alls.begin(), alls.end()), alls.end());//执行前n次插入操作for (auto item : add) {int x = find(item.first);a[x] += item.second;}//前缀和for (int i = 1; i <= alls.size(); i++) s[i] = s[i-1] + a[i];//处理后m次询问操作for (auto item : query) {int l = find(item.first);int r = find(item.second);printf("%d\n", s[r] - s[l-1]);}return 0;
}

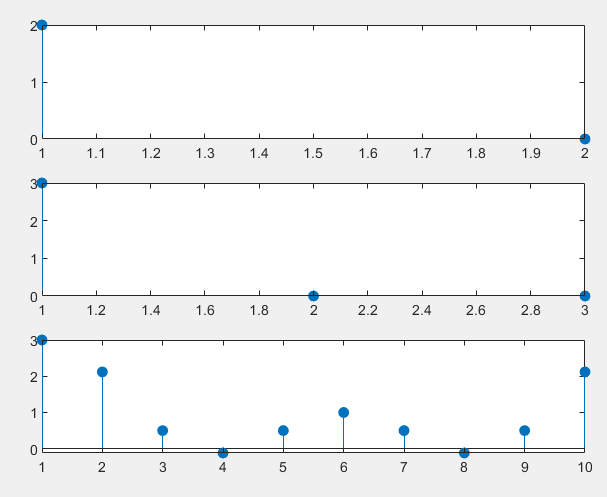
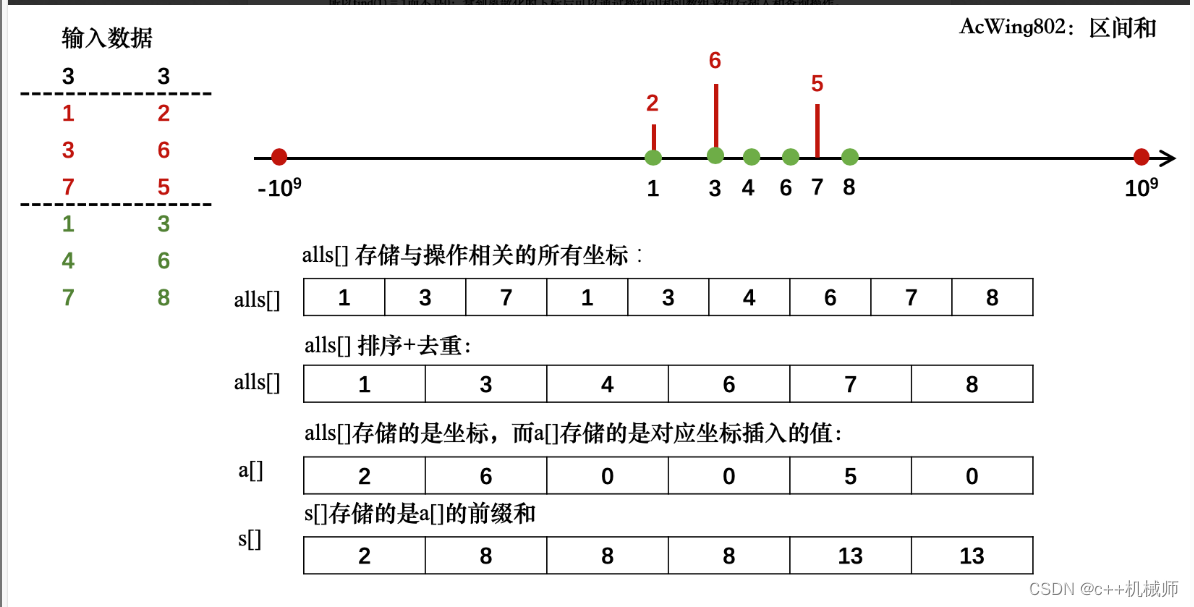
     这道题数据的值域已经达到了10^9，远远比10^5大，所以前缀和是用不了的，我们要使用离散化。我们首先将所有操作相关的数据分别存入到add和query容器中，把与操作有关的坐标存入alls容器中；接下来就是要对alls容器的数据进行排序去重的操作，这里用到了unique函数，这个函数把一个序列的重复数据从小到大放在序列末尾，并返回重复数据的第一个数据的迭代器。接下来就可以把每个坐标映射为一个自然数序列，并把它们存储的值插入到a数组中了，我们先对输入坐标进行离散化，即find函数执行的操作，这样再插入，每个值对应的下标就是一个自然数序列了，之后我们再对a数组求前缀和，执行询问操作就很简单了，这里借用两张图：

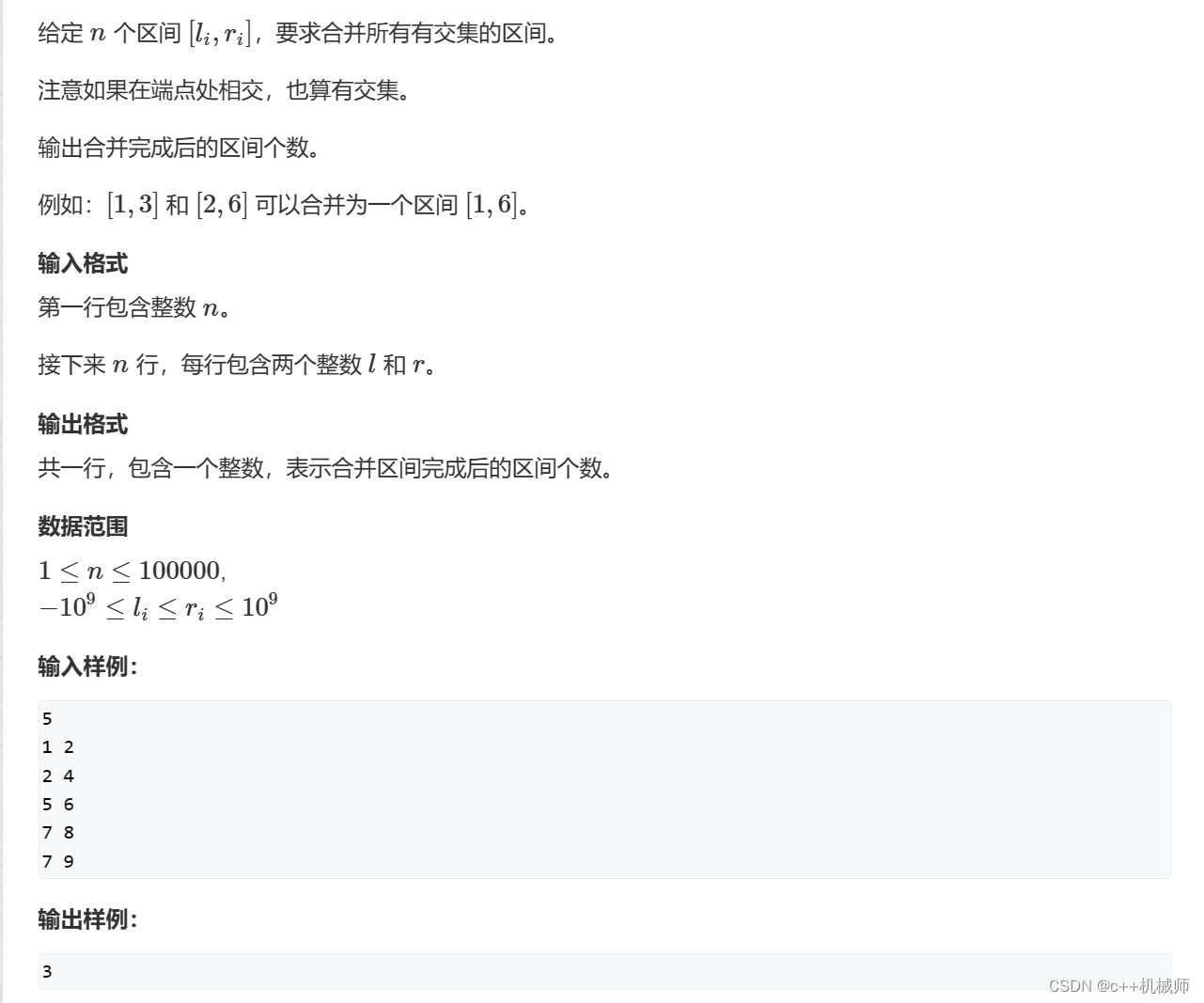
2.区间合并

     区间合并也是一种算法，主要用来合并区间，没错，就是这么简单粗暴，下面先给出模板，结合例题来领悟这种算法。

模板：

vector<PII> merge(vector<PII>& segs)
{vector<PII>res;sort(segs.begin(),segs.end());//按左端点进行排序int st=-2e9,ed=-2e9;//st表示区间左端点，ed表示区间右端点for(auto seg:segs)if(ed<seg.first)//情况1：两个区间无法合并，该区间的右端点比另一个区间的左端点还要小{if(st!=-2e9)res.push_back({st,ed});//区间1放进res数组st=seg.first,ed=seg.second;//维护区间2}else ed=max(ed,seg.second);//两个区间可以合并，且区间1不包含区间2，区间2不包含区间1//如果是区间1包含区间2，这时候不需要任何操作if(st!=-2e9)res.push_back({st,ed});//循环结束之后，st,ed变量不需要继续维护，因为这是最后一个序列，不能继续进行合并，直接放进res数组中即可return res;

       这就是区间合并的模板，下面看例题：

应用：

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;typedef pair<int,int>PII;const int N=100010;int n;
vector<PII>segs;vector<PII> merge(vector<PII>& segs)
{vector<PII>res;sort(segs.begin(),segs.end());//按左端点进行排序int st=-2e9,ed=-2e9;//st表示区间左端点，ed表示区间右端点for(auto seg:segs)if(ed<seg.first)//情况1：两个区间无法合并，该区间的右端点比另一个区间的左端点还要小{if(st!=-2e9)res.push_back({st,ed});//区间1放进res数组st=seg.first,ed=seg.second;//维护区间2}else ed=max(ed,seg.second);//两个区间可以合并，且区间1不包含区间2，区间2不包含区间1//如果是区间1包含区间2，这时候不需要任何操作if(st!=-2e9)res.push_back({st,ed});//循环结束之后，st,ed变量不需要继续维护，因为这是最后一个序列，不能继续进行合并，直接放进res数组中即可return res;
}
int main()
{cin>>n;for(int i=0;i<n;i++){int l,r;cin>>l>>r;segs.push_back({l,r});}vector<PII>res=merge(segs);cout<<res.size()<<endl;return 0;
}