链接：力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

代码：

class Solution {int[]help;  //归并排序的辅助数组public int reversePairs(int[] record) {int length=record.length;// help 数组的实例化写在递归外面，可以节省很多资源help=new int[length];return mergeSort(record,0,length-1);}//在 record 数组的 left 和 right 下标内获取逆序对的个数public int mergeSort(int[] record,int left,int right){//递归出口if(left>=right){return 0;}int ret=0;  //记录逆序对个数//int mid=(left+right)/2;int mid=(right-left)/2+left;//获取左区间[left,mid] 的逆序对个数ret+=mergeSort(record,left,mid);//获取右区间[left,mid] 的逆序对个数ret+=mergeSort(record,mid+1,right);//左边取一个数右边取一个数的逆序对个数int cur1=left,cur2=mid+1,i=0;while(cur1<=mid&&cur2<=right){if(record[cur1]>record[cur2]){ret+=mid-cur1+1;    //统计逆序对个数help[i++]=record[cur2++];}else{help[i++]=record[cur1++];}}while(cur1<=mid){help[i++]=record[cur1++];}while(cur2<=right){help[i++]=record[cur2++];}//用 help 辅助数组中的有序数据替换原数组中的数据for(int j=left;j<=right;j++){record[j]=help[j-left];}return ret;}
}

题解：

        对于该题的解法，本编博客是基于归并排序之上来进行解决的，所以清楚归并排序的流程非常重要，如果对归并排序不清晰，推荐先看归并排序（递归）

        现在我就认为大家是已经对归并排序了如指掌的，我们先来分析一下本题如何解决，如果采用暴力解法的话是很简单的，如下，用 i 指针指向下标 0 ，j 指针指向下标 1 ，判断此时 i ，j 指针指向的数据是否为逆序对，然后让 j 指针向后移动，遍历完以后再将 i 指针向后移动，j 指针在 i 指针之后重新遍历，时间复杂度为 O（n^2），这个时间复杂度在本题中是会超时的，我们得想一个更好的方法

9        7        5        4        6

i          j      

        我们要获取数组中所有的逆序对个数，可以通过中点将数据分为左边和右边两部分，先获取左边数据的所有逆序对数目 A，再获取右边数据的所有逆序对数目 B ，再获取一左一右（左边取一个数，右边取一个数）的逆序对个数 C，然后将 A+B+C 就能得到整个数组所有的逆序对个数

        其中获取左边和右边数据的逆序对个数与获取整个数组的逆序对个数所要执行的操作是相同的，就可以使用递归来解决，我们的关注点就要放在获取一左一右（左边取一个数，右边取一个数）的逆序对个数 C

        可以发现这个过程和归并排序就很像，我们可以在归并排序的过程中去记录数组中逆序对的个数

        在进行归并排序，将左右两边的数据进行合并时，左右两边的数据已经是有序的了，当左右两边的数据的顺序被修改为有序后，会影响一左一右取得的逆序对个数吗？答案是：不会，因为不管顺序如何，我们要判断的是对于左边的一个数据，右边有多少个数据小于它，至于顺序如何是没有影响的

        所以在通过归并排序将左右两边的数据排序完成进行合并时，我们可以统计一左一右的逆序对个数 C，如下图：

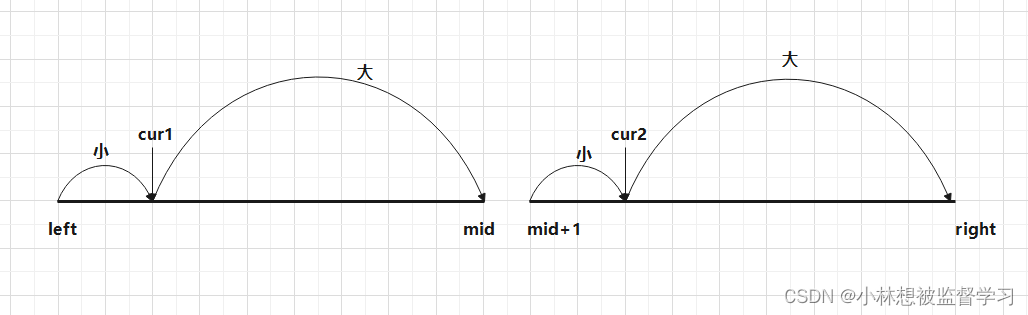
        此时数组被中点 mid 分为了【left,mid】，【mid+1，right】两个区间，左右两个区间的数据都是递增排序，用 cur1 和 cur2 指针遍历两个区间，统计一左一右的逆序对个数

        （1）.record[ cur1 ] > record[ cur2 ] ，由于左右两边的数据都是递增的，所以 cur1 右边的数据比 record[ cur1 ] 大，说明都比  record[ cur2 ] 大，代表 [ cur1,mid ] 这个区间的数据和 cur2 指针指向的数据都能构造逆序对，用 ret 记录 ret = mid - cur1 + 1，此时关于 cur2 所有的逆序对都获取到了让 cur2 ++

        （2）.record[ cur1 ] <= record[ cur2 ] ,由于 cur2 指针后面的数据都是大于 record[ cur2 ] 的，也就大于 record[ cur1 ] ，代表找不到数据能和 cur1 指针指向的数据组成逆序对，只能让 cur1++

        而在普通的归并排序中，当 cur2 指向的数小时，就要将 cur2 指向的数放到辅助数组中，cur2++，当 cur1 指向的数小时，就要将 cur1 指向的数放到辅助数组中，cur1++，我们可以发现，这与上面的分析不谋而合，所以我们可以很方便的在归并排序，归并两个有序数组的时候获取一左一右的逆序对个数

        获取逆序对的个数中 cur1<= mid 和 cur2 <= right 期间，当 cur1 或 cur2 遍历到终点后，就无法凑出逆序对了