个人主页：Lei宝啊 

愿所有美好如期而遇

---

 

本题链接

【模板】二维前缀和_牛客题霸_牛客网 

输入描述

n是行，m是列，q是查询次数，x1，y1，x2，y2是二维数组的下标。

输出描述

通过两对下标，计算这两对下标构成的这个子矩阵的和。

算法分析

算法一：暴力求解

直接遍历数组，我们考虑最坏情况就是q次查询都是从头遍历到尾，时间复杂度就是O(n*m*q)，这绝对是超时的。

算法二：前缀和

我们不希望每次查询时都要遍历去计算和，所以我们就有了创建dp表并进行预处理。

预处理二维dp表

首先我们要明白dp表每一个位置代表的状态，也就是说，dp[i][j] 就代表着从 [1,1] 到 [i,j] 这个子矩阵的和， 同时，我们创建dp表时下标从1开始，也就是说，不仅仅是数组下标从1开始，为什么要从1开始？一个是题目的m和n就是大于等于1的，另一个原因在于使用dp表进行计算时防止越界。

我们先创建这样的数组(示例一)： 

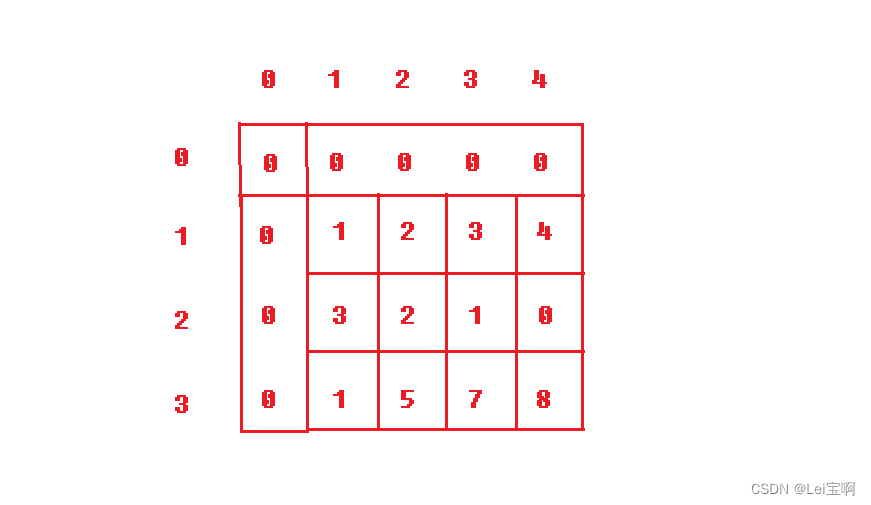
接下来就是创建dp表，并进行预处理，但是我们怎么填充dp表呢？暴力遍历吗？分析一下时间复杂度，dp表我们有m*n个元素需要填充，每个元素都代表着子矩阵的和，也就是需要遍历数组，所以整体的时间复杂度就是O(m*n*m*n)， 这样的时间复杂度甚至不如直接暴力求解，我们需要其他方法。

小学的时候，我们计算过面积，计算一块面积有时候直接算并不好算，于是我们分割了图形，求每个部分图形的和。

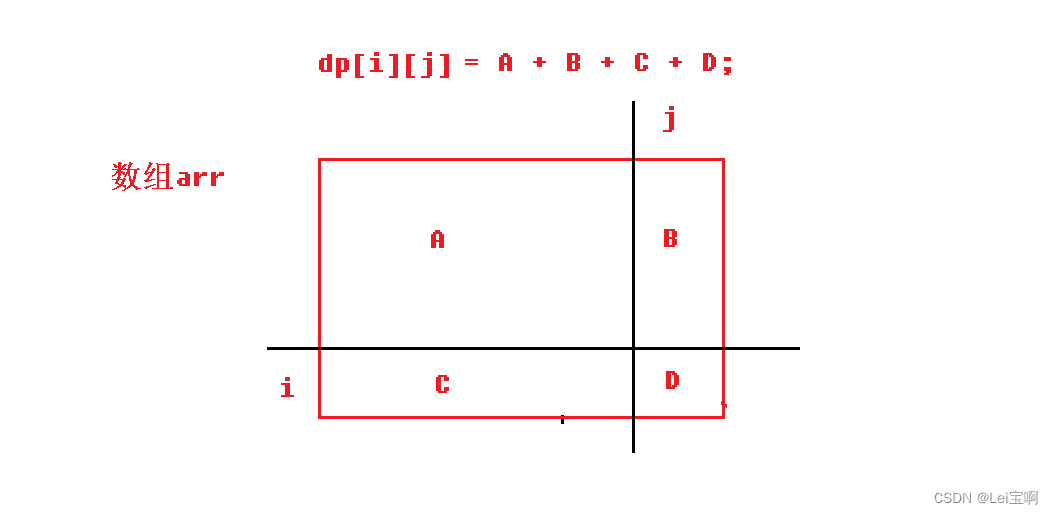
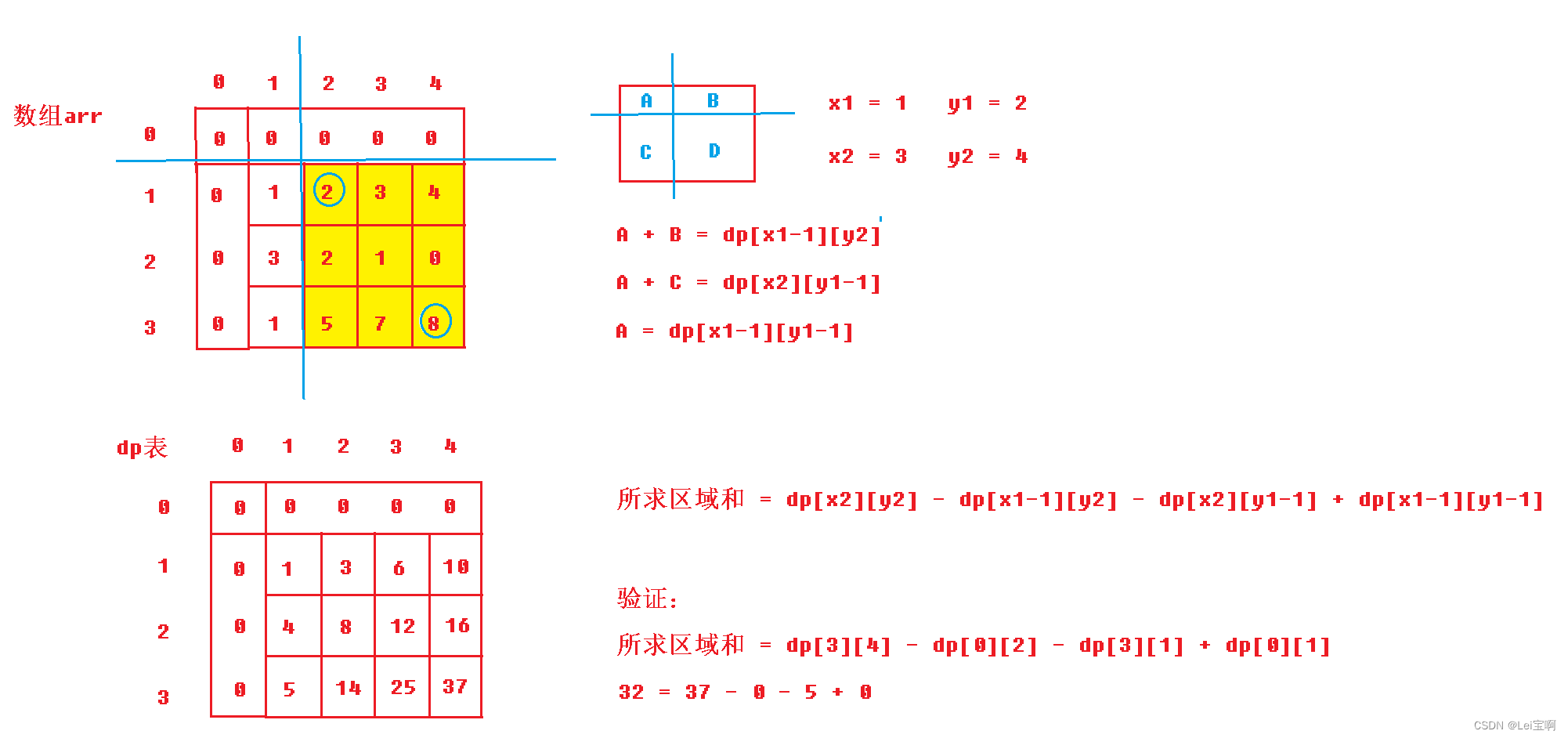
同理，直接算矩阵和不好算，我们将他分割成A，B，C，D四块，dp[i][j]的值就是A + B + C + D，但是我们发现A好算，就是dp[i-1][j-1]，B和C并不好算，但是A+B呢？A+C呢？

所以我们也就有了思路：

最终我们得到dp表：

 

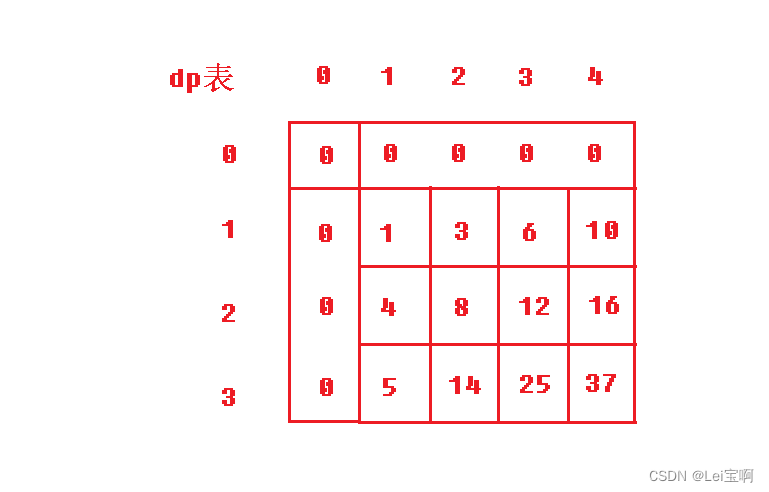
使用dp表计算

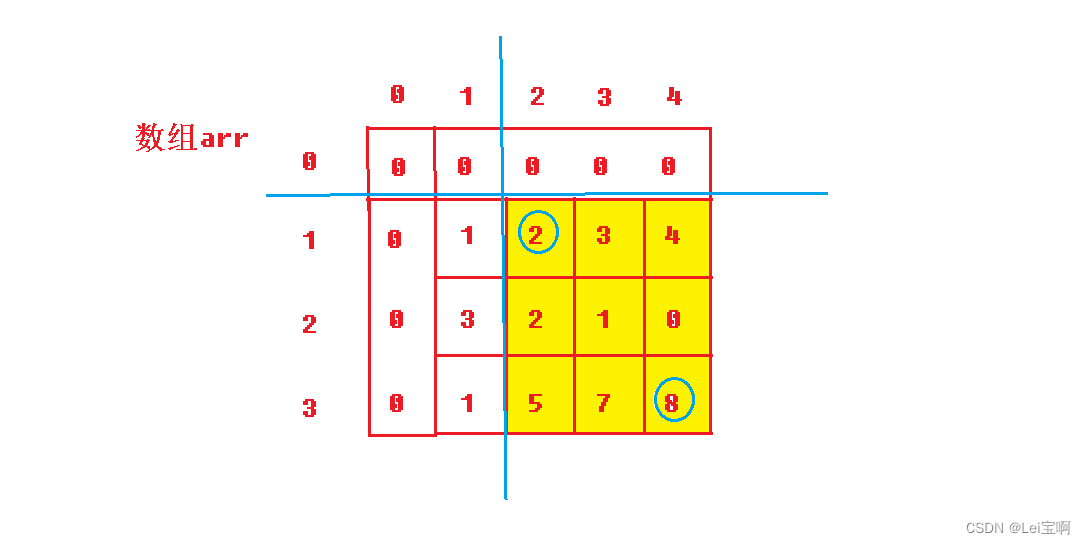
现在我们有了[1,1]到任意一个下标这个子矩阵的和，现在我们要算任意两个下标构成的子矩阵的和，我们看图：

我们似乎仍然能像面积一样进行分割：

 

解题源码

#include <iostream>
#include <vector>
using namespace std;int main() 
{//n行，m列，q次int n, m, q;cin >> n >> m >> q;//创建二维数组vector<vector<int>> vv(n+1,vector<int>(m+1, 0));for(int i=1; i<n+1; i++){for(int j=1; j<m+1; j++){cin >> vv[i][j];}}//创建dp表并填充vector<vector<long long>> dp(n+1,vector<long long>(m+1, 0));for(int i=1; i<n+1; i++){for(int j=1; j<m+1; j++){dp[i][j] = dp[i-1][j] +dp[i][j-1] - dp[i-1][j-1] + vv[i][j];}}while(q--){int x1, y1, x2, y2;cin >> x1 >> y1 >> x2 >> y2;long long sum = dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] +dp[x1-1][y1-1];cout << sum << endl;}}
// 64 位输出请用 printf("%lld")