回溯搜索的通用算法的问题与改进思路
• 需改善无信息回溯搜索算法的性能。
• 通用改进方法的思路:
– 下一步该给哪个变量赋值, 按什么顺序给该变量赋值?
– 每步搜索应该做怎样的推理? 当前变量的赋值会对其他未赋值变量产生什么约束, 怎样利用这种约束以提高效率。
– 当遇到某个失败的变量赋值时, 怎样避免同样的失败? 就是说如何找到对这种失败起到关键作用的某个变量赋值。
下面介绍基于变量和赋值次序的启发式的三种方法。
MRV(最少剩余值) 启发式
由于随机的变量赋值排序难以产生高效率的搜索。
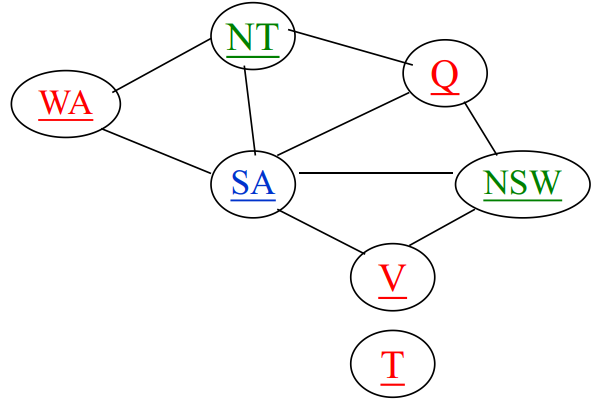
例如: 在WA=red且NT=green条件下选取SA赋值的可能(只能取blue)与Q能取到的赋值(可以取blue、red)的比为(1:2), 并且一旦给定SA赋值以后, Q、 NSW和V的赋值只有一个选择。
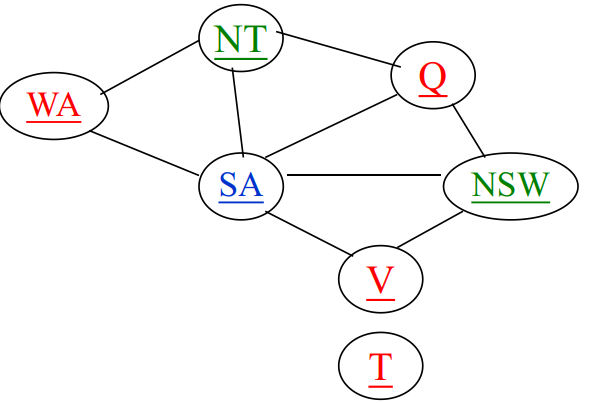
因此, 应当选择合法取值最少的变量, 即最少剩余值(MRV)启发式,也称为最受约束变量启发式或失败优先启发式。
为失败优先启发式是因为它可以很快找到失败的变量, 从而引起搜索的剪枝, 避免更多导致同样失败的搜索。
最少约束值启发式
最少约束值启发式: 当赋值的变量有多个值选择时, 优先的值应是约束图中排除邻居变量的可选值最少的, 即优先选择为剩余变量的赋值留下最多选择的赋值。
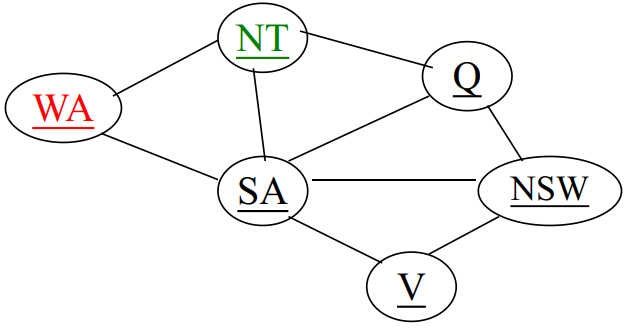
例如, WA=red且NT=green时, 如果给Q赋值, 可以为blue或red, 而Q=blue的选择不好, 因为此时SA没有一个可选择的了。所以应该让Q=red,使得SA留下他最多的选择。
度启发式
度启发式: 选择涉及对其他未赋值变量的约束数量大(与其他变量关联最多) 的变量。

– 地图染色例子中, 度(SA)=5, 其他均为2或3。
– 实际上, 一旦选择了SA作为初始节点, 应用度启发式求解本问题, 则可以不经任何回溯就找到解。