目录

题目地址：

题目：

我们直接看题解吧：

解题方法：

方法分析：

解题分析：

解题思路：

代码实现：

代码补充说明：

---

题目地址：

102. 二叉树的层序遍历 - 力扣（LeetCode）

难度：中等

今天刷二叉树的层序遍历，大家有兴趣可以点上看看题目要求，试着做一下。

题目：

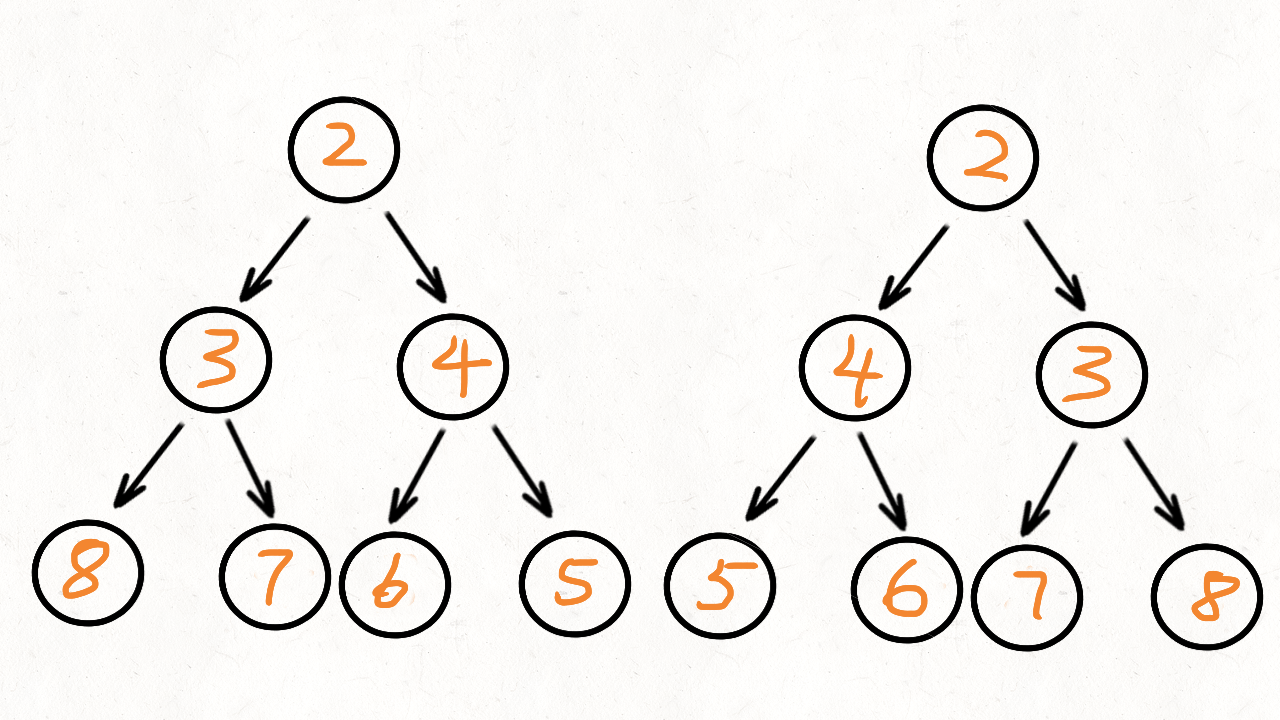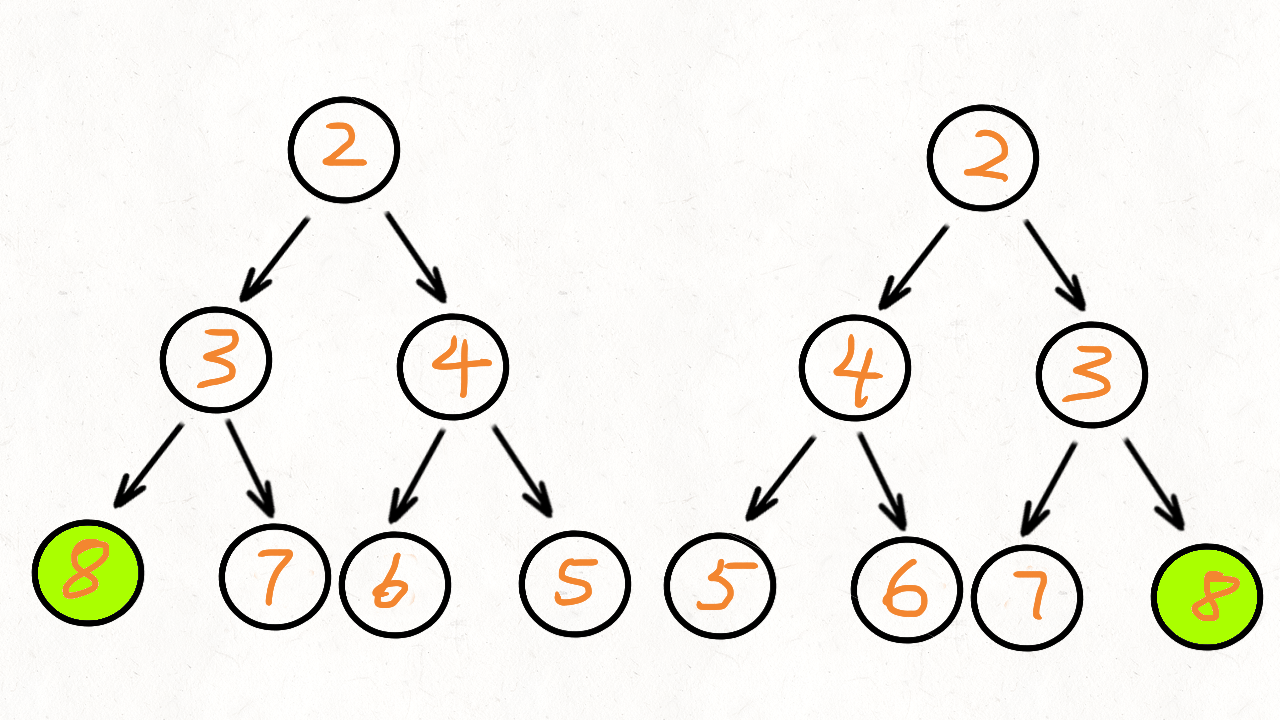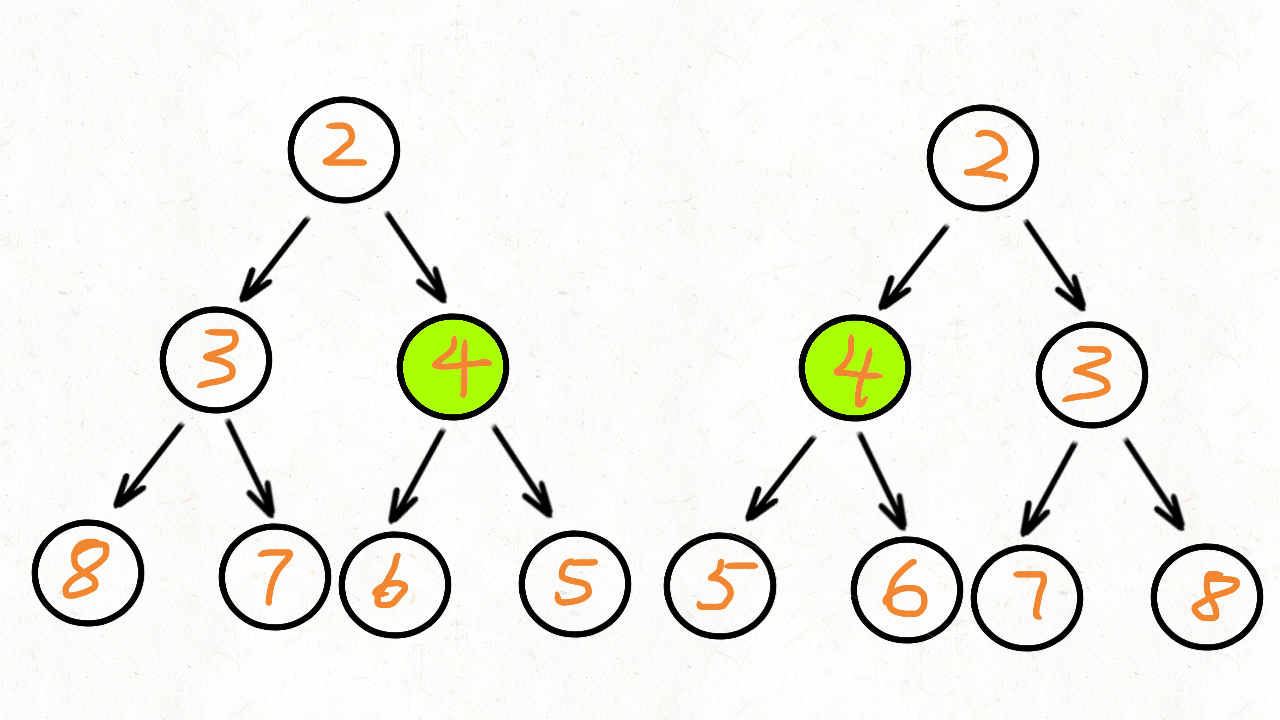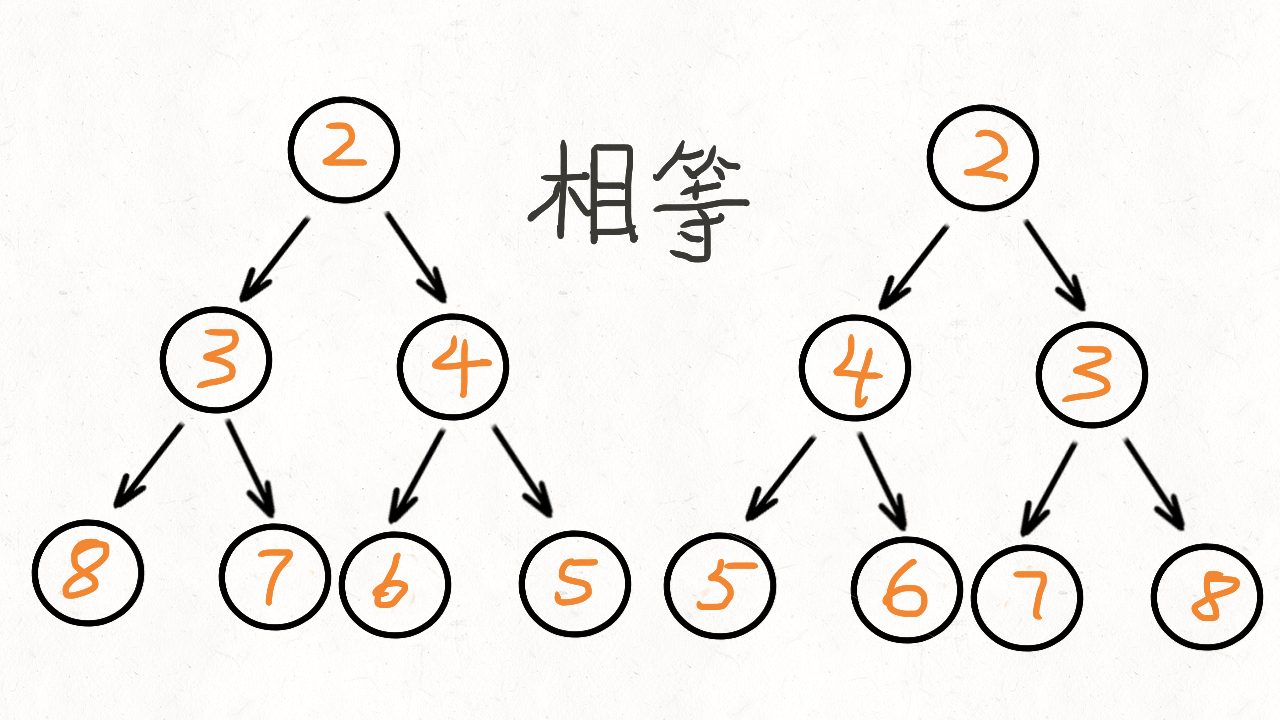
给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

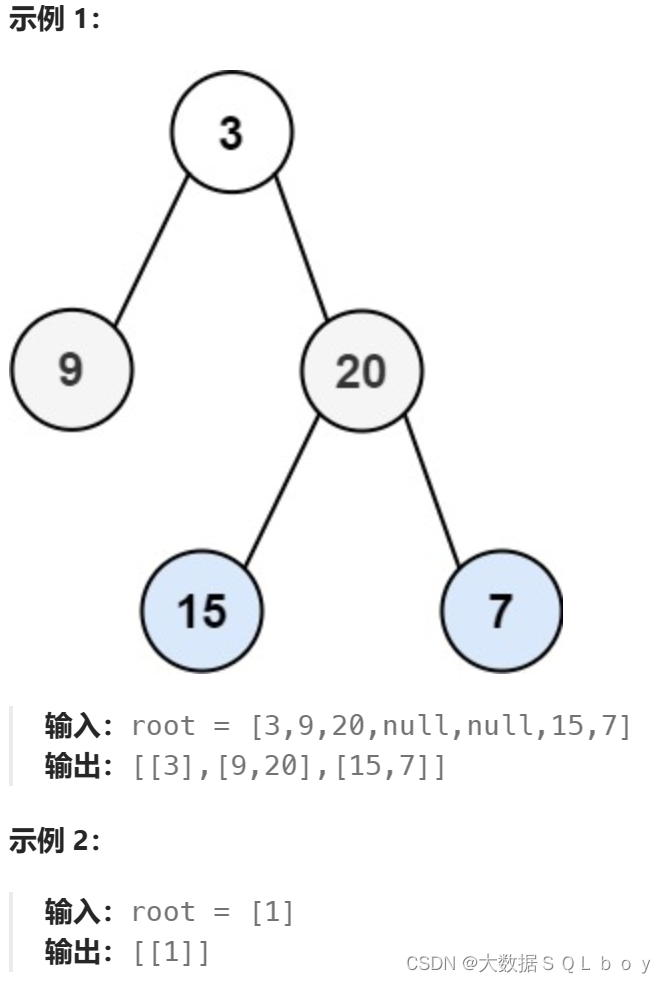
我们直接看题解吧：

解题方法：

利用方法为广度优先遍历算法(BFS)

方法分析：

      DFS（深度优先搜索）和 BFS（广度优先搜索）就像孪生兄弟，提到一个总是想起另一个。然而在实际使用中，我们用 DFS 的时候远远多于 BFS。那么，是不是 BFS 就没有什么用呢？

       如果我们使用 DFS/BFS 只是为了遍历一棵树、一张图上的所有结点的话，那么 DFS 和 BFS 的能力没什么差别，我们当然更倾向于更方便写、空间复杂度更低的 DFS 遍历。不过，某些使用场景是 DFS 做不到的，只能使用 BFS 遍历。比如层序遍历、最短路径。

      实际上，「BFS 遍历」、「层序遍历」、「最短路径」实际上是递进的关系。在 BFS 遍历的基础上区分遍历的每一层，就得到了层序遍历。在层序遍历的基础上记录层数，就得到了最短路径。

解题分析：

       对于这道题，我们可以想到最朴素的方法是用一个二元组 (node, level) 来表示状态，它表示某个节点和它所在的层数，每个新进队列的节点的层数 level 值都是父亲节点的层数 level 值加一。最后根据每个点的层数 level 对点进行分类，分类的时候我们可以利用哈希表，维护一个以层数 level 为键，对应节点值组成的数组为值，广度优先搜索结束以后按键 level 从小到大取出所有值，组成答案返回即可。

      但是考虑优化空间开销，不用哈希映射，并且只用一个变量 node 表示状态，因此可以利用队列实现这个功能

           ·首先根元素入队

           ·当队列不为空的时候

           ·求当前队列的长度 依次从队列中取si个元素进行拓展，然后进入下一次迭代

      它和普通广度优先搜索的区别在于，普通广度优先搜索每次只取一个元素拓展，而这里每次取si个元素。

解题思路：

1、创建双端给队列queue放当前层的节点，创建二维数组res保存遍历所得的节点结果

 2、进行初始化，在队列queue中添加root(若非空)

3、BFS循环，当队列queue空时结束循环

            a.新建一个临时表tmp，用于存储当前层的打印结果

           b.当前层打印循环： 循环次数为当前层节点数（即队列 queue 长度）。

               ·出队： 取队首节点，记为 node,。

               ·打印： 将节点值node.val 添加至 tmp 尾部。

             · 更新queue： 若 node 的左（右）子节点不为空，则将左（右）子节点加入队列    queue 。即将当前层每个节点子节点放入queue

          c.将当前层结果 tmp 添加入 res 。

4、返回值： 返回打印结果列表 res 即可。

代码实现：

class Solution {public List<List<Integer>> levelOrder(TreeNode root) {Queue<TreeNode> queue = new LinkedList<>();//创建双端队列queueList<List<Integer>> res = new ArrayList<>();//创建二维列表resif (root != null) queue.add(root);       //将root节点加到队列中while (!queue.isEmpty()) {//队列空时退出循环List<Integer> tmp = new ArrayList<>();//新建临时数组tmpfor(int i = queue.size(); i > 0; i--) {//当前层的循环遍历TreeNode node = queue.poll();//取出一个节点进行遍历tmp.add(node.val);         //将节点值加到tmpif (node.left != null) queue.add(node.left);//非空则遍历该节点的左子树if (node.right != null) queue.add(node.right);//非空则遍历该节点的右子树}res.add(tmp);//当前层节点值加到res}return res;//返回树的遍历结果}
}

代码补充说明：

1、代码中实际上对树进行了非空的判断，若为空，则会返回空表res=[ ]

2、在当前层for循环中：

              初始值是每个队列的长度（会发生变化），然后递减，

            而这样做好处在于，下面我更新队列 queue的元素时，它不会影响我遍历当前层的的节点数，因为for循环初始化只执行一次