目录
一、向量定义
二、计算向量
三、向量的加法(连续行走)
四、向量的长度
五、单位向量
六、向量的点积
1 计算
2 作用
七、向量的叉乘
1 承上启下
2 叉乘结论
3 叉乘的计算(这里看不懂就百度叉乘计算)
八、欢迎收看Shader专栏
一、向量定义
向量:从一个点到另一个点的箭头。
例:假如现在有两个点,A(0,0)和B点(4,5)。
假如从A走向B(如图1),箭头为:

假如从B走向A(如图2),箭头为:
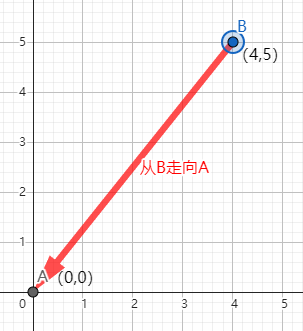
我们会用A(0,0)表示点A,
我们会用B(4,5)表示点B,
问题,我们用什么表示和区分这两个箭头?
答:如果从A走向B,我们就写成
,如果从B走向A,就写成
(是不是很形象)。
字母确定了,可数字怎么办?
答:因为横坐标x是向左为正,纵坐标y是向上为正。
我们从A(0,0)走向B(4,5)等于向右走4格,向上走5格,所以是
(4,5),
反之,如果从B(4,5)走向A(0,0)等于向左走4格,向下走5格,所以是
(-4,-5),
所以在表达向量时,写的是箭头起点到箭头终点是如何走过去。
二、计算向量
(如图3)如果我们随意画出两个点A(1,3),B(4,5)

通过数格子,我们可以得出(3,2),但这个数字,我们也可以算出来,通过终点的B(4,5)中的x减去A(1,3)的x:4-1=3,通过终点的B(4,5)中的y减去A(1,3)的y:5-3=2
也可以得出:(3,2)
所以:终点的坐标,减去起点的坐标,就是向量的数值
三、向量的加法(连续行走)
(如图4)我们画两个连着的向量(1,3)和
(3,2):

从图中(如图5)我们可以看出,我们从A走到B,又从B走到C,这种连着走的向量我们可以相加,实际上两个向量就是从A走到了C,横着向右走了4格,向上走了5格。
(1,3)+
(3,2)=
(1+3,3+2)=
(4,5)

四、向量的长度
(如图6)假如我希望计算(4,5)的长度,通过我们学过的勾股定理就得出
AC =

所以:向量的长度为
五、单位向量
单位向量:向量长度是1
把任何一个向量变成单位向量,只需要除以向量的长度。
例:向量(3,4),长度是5,希望长度变为1,就直接集体除以5。
所以,向量(3,4)的单位向量就是(3/5,4/5)。
六、向量的点积
1 计算
设向量a(1,2)和向量b(3,4)点乘
算法1:
算法2:
算法2算到这一步就停了,因为不知道cosθ,
可是算法1和算法2的结果是相同的。
所以,可以算出
最后θ≈11.5°
2 作用
为啥要算点积?(我们把上面的向量a和向量b画出来)(如图7)

我原本面向A(向量a),现在我想面向B,我应该旋转多少度?
答:刚才算过了:11.5°
备注(以下结论的推导过程自己百度):
>0 a和b的夹角0-90度之间
=0 a和b的夹角为90度
<0 a和b的夹角大于90度
七、向量的叉乘
1 承上启下
第六部分我们知道了旋转角度,不知道聪明的你有没有发现,其实,你只知道了角度,不知道是顺时针旋转还是逆时针旋转。叉乘就事帮助我们判断是哪个方向的旋转的。
2 叉乘结论
当叉乘结果<0 顺时针旋转
当叉乘结果>0 逆时针旋转
叉乘结果=0 不用旋转
3 叉乘的计算(这里看不懂就百度叉乘计算)
我们还是计算向量a(1,2)和向量b(3,4)叉乘,因为叉乘需要x,y,z才能计算,此时相当于我们的z是0,所以我们的向量为a(1,2,0)和向量b(3,4,0)。
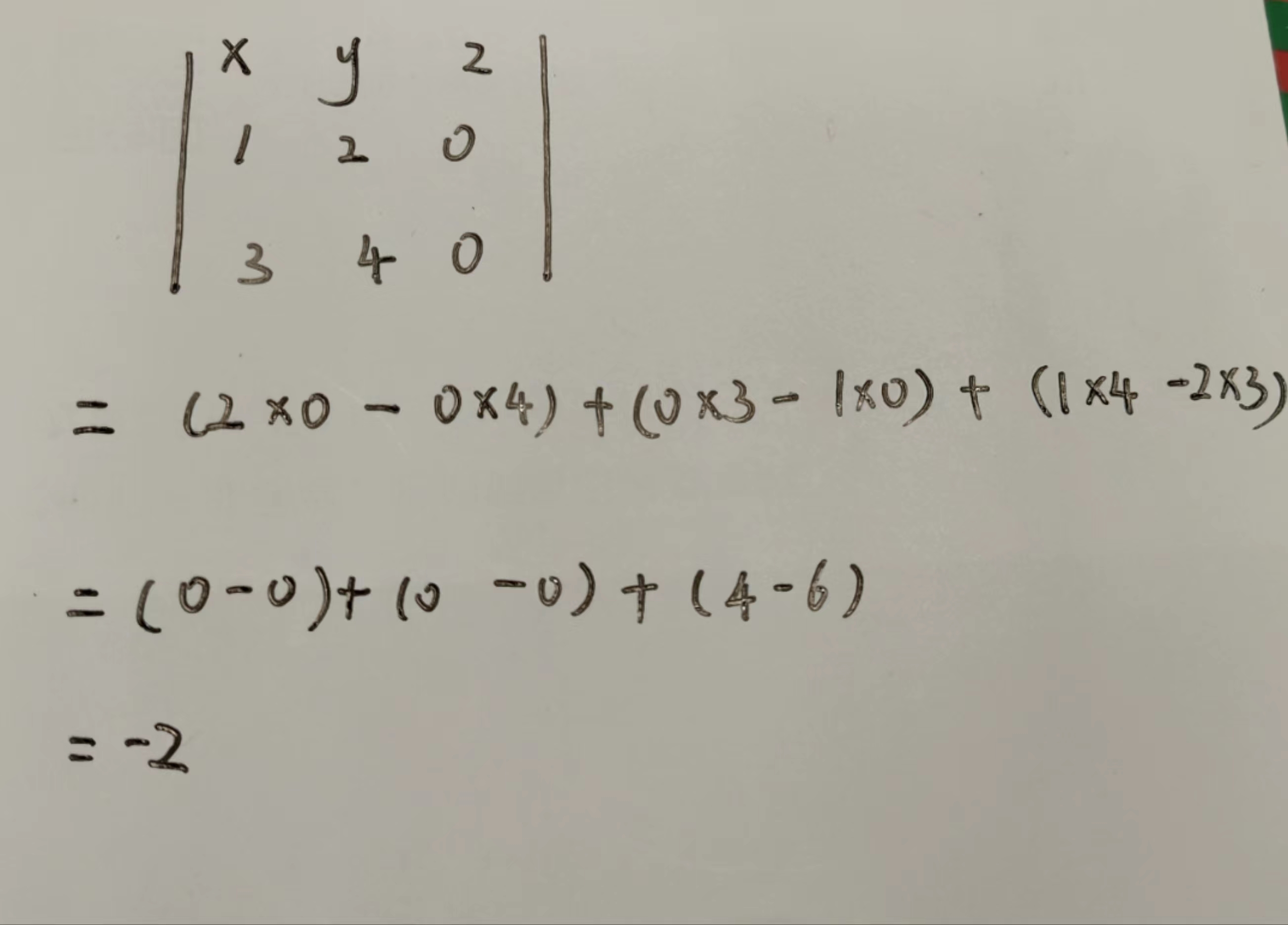
此时是-2<0所以,我们只需要逆时针旋转11.5°,就可以从向量a的方向变成向量b的方向。
八、欢迎收看Shader专栏
https://blog.csdn.net/weixin_49427945/category_12525804.html