引言
这是Transformer的第二篇文章,上篇文章中我们了解了分词算法BPE,本文我们继续了解Transformer中的位置编码和核心模块——多头注意力。
位置编码
我们首先根据BPE算法得到文本切分后的子词标记,然后经过输入嵌入层将每个标记转换为对应的向量表示,但Transformer不再基于类似RNN循环的方式,而是可以一次为所有的标记进行建模,因此丢失了输入中单词之间的相对位置关系。
在真正喂给Transformer模型之前,一个重要的操作是为嵌入向量表示增加位置表示,即位置编码。位置变可以通过学习得到也可以通过固定设置,这里介绍Transformer原始论文中使用的基于正弦函数和余弦函数的固定位置编码。
一个好的位置编码应该具有以下性质:
- 每个时间步(位置)的编码应该唯一;
- 任意两个时间步的距离应该与句子长度无关;
- 取值应该是有界的;
我们从这几个方面来分析下Transformer中使用的位置编码:
PE ( pos , 2 i ) = sin ( pos 1000 0 2 i / d ) (1) \text{PE}(\text{pos},2i) = \sin(\frac{\text{pos}}{10000^{2i/d}}) \tag 1 PE(pos,2i)=sin(100002i/dpos)(1)
PE ( pos , 2 i + 1 ) = cos ( pos 1000 0 2 i / d ) (2) \text{PE}(\text{pos},2i+1) = \cos(\frac{\text{pos}}{10000^{2i/d}}) \tag 2 PE(pos,2i+1)=cos(100002i/dpos)(2)
其中 pos \text{pos} pos表示标记所在的位置,假设取值从0~100; i i i代表维度,即位置编码的每个维度对应一个波长不同的正弦或余弦波,波长从 2 π 2\pi 2π到 10000 ⋅ 2 π 10000\cdot 2\pi 10000⋅2π成等比数列; d d d表示位置编码的最大维度,和词嵌入的维度相同,假设是512;
这里假设最长时间步(位置)为100,每个位置的编码都是一个512维度的向量。我们先来回顾下常规正余弦函数 sin ( x ) \sin(x) sin(x)和 cos ( x ) \cos(x) cos(x)的图像:
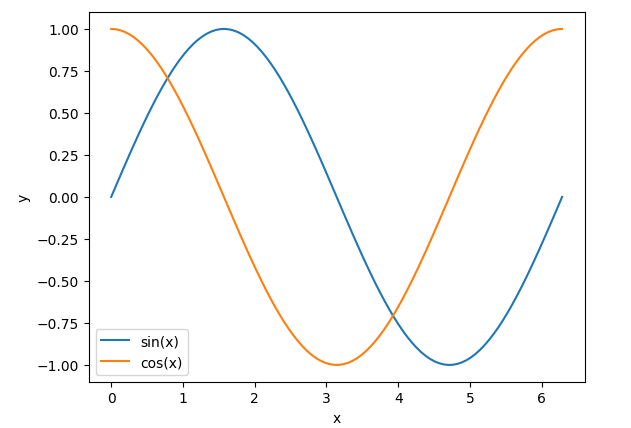
正余弦函数的图像如上图所示,显然它的取值是有界的,取值范围在[-1,+1]。但Transformer用的正弦函数的波长不同。
对于每个位置,由于我们有512个维度,因此我们有256对正弦值和余弦值, i i i的取值在[0,255]。假设考虑所有维度,计算位置 pos \text{pos} pos处的位置编码向量每个元素(维度)的值:
PE ( pos , 0 ) = sin ( pos 1000 0 0 512 ) PE ( pos , 1 ) = cos ( pos 1000 0 0 512 ) PE ( pos , 2 ) = sin ( pos 1000 0 2 512 ) PE ( pos , 3 ) = cos ( pos 1000 0 2 512 ) PE ( pos , 4 ) = sin ( pos 1000 0 4 512 ) PE ( pos , 5 ) = cos ( pos 1000 0 4 512 ) ⋮ PE ( pos , 510 ) = sin ( pos 1000 0 510 512 ) PE ( pos , 511 ) = cos ( pos 1000 0 510 512 ) \begin{aligned} \text{PE}(\text{pos}, 0) &= \sin\left( \dfrac{\text{pos}}{10000^{\frac{0}{512}}} \right) \\ \text{PE}(\text{pos}, 1) &= \cos\left( \dfrac{\text{pos}}{10000^{\frac{0}{512}}} \right) \\ \text{PE}(\text{pos}, 2) &= \sin\left( \dfrac{\text{pos}}{10000^{\frac{2}{512}}} \right) \\ \text{PE}(\text{pos}, 3) &= \cos\left( \dfrac{\text{pos}}{10000^{\frac{2}{512}}} \right) \\ \text{PE}(\text{pos}, 4) &= \sin\left( \dfrac{\text{pos}}{10000^{\frac{4}{512}}} \right) \\ \text{PE}(\text{pos}, 5) &= \cos\left( \dfrac{\text{pos}}{10000^{\frac{4}{512}}} \right) \\ \vdots \\ \text{PE}(\text{pos}, 510) &= \sin\left( \dfrac{\text{pos}}{10000^{\frac{510}{512}}} \right) \\ \text{PE}(\text{pos}, 511) &= \cos\left( \dfrac{\text{pos}}{10000^{\frac{510}{512}}} \right) \\ \end{aligned} PE(pos,0)PE(pos,1)PE(pos,2)PE(pos,3)PE(pos,4)PE(pos,5)⋮PE(pos,510)PE(pos,511)=sin(100005120pos)=cos(100005120pos)=sin(100005122pos)=cos(100005122pos)=sin(100005124pos)=cos(100005124pos)=sin(10000512510pos)=cos(10000512510pos)
对于位置0的编码为:
PE ( 0 ) = ( sin ( 0 1000 0 0 512 ) , cos ( 0 1000 0 0 512 ) , sin ( 0 1000 0 2 512 ) , cos ( 0 1000 0 2 512 ) , … , sin ( 0 1000 0 510 512 ) , cos ( 0 1000 0 510 512 ) ) = ( sin ( 0 ) , cos ( 0 ) , sin ( 0 ) , cos ( 0 ) , … , sin ( 0 ) , cos ( 0 ) ) = ( 0 , 1 , 0 , 1 , … , 0 , 1 ) \begin{aligned} \text{PE}(0) &= {\tiny \left( \sin\left( \dfrac{0}{10000^{\frac{0}{512}}} \right), \cos\left( \dfrac{0}{10000^{\frac{0}{512}}} \right), \sin\left( \dfrac{0}{10000^{\frac{2}{512}}} \right), \cos\left( \dfrac{0}{10000^{\frac{2}{512}}} \right), \dots, \sin\left( \dfrac{0}{10000^{\frac{510}{512}}} \right), \cos\left( \dfrac{0}{10000^{\frac{510}{512}}} \right) \right)} \\ &= (\sin(0), \cos(0), \sin(0), \cos(0), \dots, \sin(0), \cos(0)) \\ &= (0, 1, 0, 1, \dots, 0, 1) \end{aligned} PE(0)=(sin(1000051200),cos(1000051200),sin(1000051220),cos(1000051220),…,sin(100005125100),cos(100005125100))=(sin(0),cos(0),sin(0),cos(0),…,sin(0),cos(0))=(0,1,0,1,…,0,1)
是一个交替0和1的向量;
对于位置1的编码为:
PE ( 1 ) = ( sin ( 1 1000 0 0 512 ) , cos ( 1 1000 0 0 512 ) , sin ( 1 1000 0 2 512 ) , cos ( 1 1000 0 2 512 ) , … , sin ( 1 1000 0 510 512 ) , cos ( 1 1000 0 510 512 ) ) = ( 0.8414 , 0.5403 , 0.8218 , 0.5696 , … , 0.0001 , 0.9999 ) \begin{aligned} \text{PE}(1) &= {\tiny \left( \sin\left( \dfrac{1}{10000^{\frac{0}{512}}} \right), \cos\left( \dfrac{1}{10000^{\frac{0}{512}}} \right), \sin\left( \dfrac{1}{10000^{\frac{2}{512}}} \right), \cos\left( \dfrac{1}{10000^{\frac{2}{512}}} \right), \dots, \sin\left( \dfrac{1}{10000^{\frac{510}{512}}} \right), \cos\left( \dfrac{1}{10000^{\frac{510}{512}}} \right) \right)} \\ &= (0.8414, 0.5403, 0.8218, 0.5696, \dots, 0.0001, 0.9999) \end{aligned} PE(1)=(sin(1000051201),cos(1000051201),sin(1000051221),cos(1000051221),…,sin(100005125101),cos(100005125101))=(0.8414,0.5403,0.8218,0.5696,…,0.0001,0.9999)
这里位置索引 pos \text{pos} pos为 sin ( x ) \sin(x) sin(x)中的自变量 x x x。上面说位置编码的每个维度对应一个波长不同的正弦或余弦波,波长从 2 π 2\pi 2π到 10000 ⋅ 2 π 10000\cdot 2\pi 10000⋅2π成等比数列。对于第0个维度,它们的波长都为 2 π 1 = 2 π \frac{2\pi}{1}=2\pi 12π=2π;对于最后一个维度,即510(不会取到512,因为索引从0开始),波长约等于 2 π ⋅ 10000 2\pi \cdot 10000 2π⋅10000,这里令 510 512 ≈ = 1 \frac{510}{512} \approx =1 512510≈=1。
波长就是一个周期的距离,波长越长,走过一个周期越缓慢。单纯看这些数字没有意义,下面尝试可视化它们。
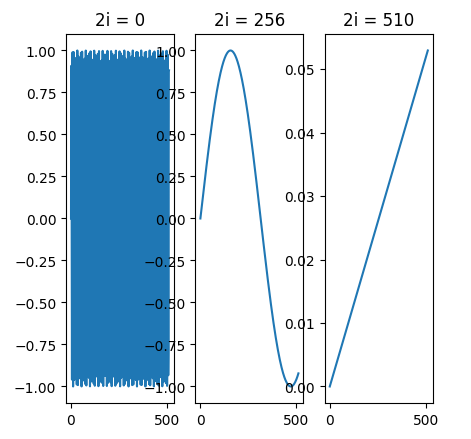
上图分别表示位置 pos \text{pos} pos从0到512的过程中,不同波长的函数图像。上图左表示维度0波长 2 π 2\pi 2π的图像,可以看到在0到1之间疯狂地变化;而上图右对应 10000 ⋅ 2 π 10000\cdot 2\pi 10000⋅2π的波长,从0变化到0.06,波动非常小。
从这里我们可知满足了性质1和3,性质3好理解,取值在[-1,1]之间,是有界的。如果理解满足性质1呢?
假设我们想用二进制格式表示一个数字:
0 : 0 0 0 0 8 : 1 0 0 0 1 : 0 0 0 1 9 : 1 0 0 1 2 : 0 0 1 0 10 : 1 0 1 0 3 : 0 0 1 1 11 : 1 0 1 1 4 : 0 1 0 0 12 : 1 1 0 0 5 : 0 1 0 1 13 : 1 1 0 1 6 : 0 1 1 0 14 : 1 1 1 0 7 : 0 1 1 1 15 : 1 1 1 1 \begin{align} 0: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{0}} & & 8: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{0}} \\ 1: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{1}} & & 9: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{1}} \\ 2: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{0}} & & 10: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{0}} \\ 3: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{1}} & & 11: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{1}} \\ 4: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{0}} & & 12: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{0}} \\ 5: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{1}} & & 13: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{1}} \\ 6: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{0}} & & 14: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{0}} \\ 7: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{1}} & & 15: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{1}} \\ \end{align} 0: 0 0 0 01: 0 0 0 12: 0 0 1 03: 0 0 1 14: 0 1 0 05: 0 1 0 16: 0 1 1 07: 0 1 1 18: 1 0 0 09: 1 0 0 110: 1 0 1 011: 1 0 1 112: 1 1 0 013: 1 1 0 114: 1 1 1 015: 1 1 1 1
我们通过4位就可以表示最多到十进制15,我们可以发现不同位之间的变化率,第0位(红色)在每个数字上交替变化;第1位(蓝色)在每两个数字上重复;最高位(橙色)每八个数字上变化一次。
而Transformer不同波长(频率)的正余弦,所达到的效果是类似的。

或者可以理解为时钟上的指针(对应3个维度),波长(频率)对应指针的转速,秒针转速最快,就是第0位;时针转速最慢就是最高一位。在最高一位的周期内是不会重复的。所以性质3满足。
我们来看性质2,其实意思就是可以体现相对位置关系, pos + k \text{pos} +k pos+k的位置编码可以被位置 pos \text{pos} pos线性表示。这里需要用到三角函数公式:
sin ( α + β ) = sin α cos β + cos α sin β cos ( α + β ) = cos α cos β – sin α sin β \begin{align} \sin \left( {\alpha + \beta } \right) &= \sin \alpha \cos \beta + \cos \alpha \sin \beta\\ \cos \left( {\alpha + \beta } \right) &= \cos \alpha \cos \beta – \sin \alpha \sin \beta \end{align} sin(α+β)cos(α+β)=sinαcosβ+cosαsinβ=cosαcosβ–sinαsinβ
为了简便,令 w i = 1 1000 0 2 i / d w_i=\frac{1}{10000^{2i/d}} wi=100002i/d1,有
PE ( pos , 2 i ) = sin ( w i ⋅ pos ) (3) \text{PE}(\text{pos},2i) = \sin(w_i \cdot \text{pos}) \tag 3 PE(pos,2i)=sin(wi⋅pos)(3)
PE ( pos , 2 i + 1 ) = cos ( w i ⋅ pos ) (4) \text{PE}(\text{pos},2i+1) = \cos(w_i \cdot \text{pos}) \tag 4 PE(pos,2i+1)=cos(wi⋅pos)(4)
对于 pos + k \text{pos} +k pos+k的位置编码:
PE ( pos + k , 2 i ) = sin ( w i ⋅ ( pos + k ) ) = sin ( w i ⋅ pos ) cos ( w i ⋅ k ) + cos ( w i ⋅ pos ) sin ( w i ⋅ k ) PE ( pos + k , 2 i + 1 ) = cos ( w i ⋅ ( pos + k ) ) = cos ( w i ⋅ pos ) cos ( w i ⋅ k ) − sin ( w i ⋅ pos ) sin ( w i ⋅ k ) \begin{aligned} \text{PE}(\text{pos} + k,2i) &= \sin(w_i \cdot (\text{pos} + k)) = \sin(w_i \cdot \text{pos})\cos(w_i\cdot k) + \cos(w_i\cdot \text{pos})\sin(w_i \cdot k)\\ \text{PE}(\text{pos} + k,2i+1) &= \cos(w_i \cdot (\text{pos} + k)) = \cos(w_i \cdot \text{pos})\cos(w_i\cdot k) - \sin(w_i\cdot \text{pos})\sin(w_i \cdot k) \end{aligned} PE(pos+k,2i)PE(pos+k,2i+1)=sin(wi⋅(pos+k))=sin(wi⋅pos)cos(wi⋅k)+cos(wi⋅pos)sin(wi⋅k)=cos(wi⋅(pos+k))=cos(wi⋅pos)cos(wi⋅k)−sin(wi⋅pos)sin(wi⋅k)
根据式 ( 3 ) (3) (3)和 ( 4 ) (4) (4)整理上式有:
PE ( pos + k , 2 i ) = sin ( w i ⋅ ( pos + k ) ) = PE ( pos , 2 i ) cos ( w i ⋅ k ) + PE ( pos , 2 i + 1 ) sin ( w i ⋅ k ) PE ( pos + k , 2 i + 1 ) = cos ( w i ⋅ ( pos + k ) ) = PE ( pos , 2 i + 1 ) cos ( w i ⋅ k ) − PE ( pos , 2 i ) sin ( w i ⋅ k ) \begin{aligned} \text{PE}(\text{pos} + k,2i) &= \sin(w_i \cdot (\text{pos} + k)) = \text{PE}(\text{pos},2i)\cos(w_i\cdot k) + \text{PE}(\text{pos},2i+1)\sin(w_i \cdot k)\\ \text{PE}(\text{pos} + k,2i+1) &= \cos(w_i \cdot (\text{pos} + k)) =\text{PE}(\text{pos},2i+1)\cos(w_i\cdot k) - \text{PE}(\text{pos},2i)\sin(w_i \cdot k) \end{aligned} PE(pos+k,2i)PE(pos+k,2i+1)=sin(wi⋅(pos+k))=PE(pos,2i)cos(wi⋅k)+PE(pos,2i+1)sin(wi⋅k)=cos(wi⋅(pos+k))=PE(pos,2i+1)cos(wi⋅k)−PE(pos,2i)sin(wi⋅k)
由于 pos \text{pos} pos和 pos + k \text{pos} +k pos+k的相对距离 k k k是常数,即 u = cos ( w i ⋅ k ) u=\cos(w_i\cdot k) u=cos(wi⋅k)和 v = sin ( w i ⋅ k ) v=\sin(w_i\cdot k) v=sin(wi⋅k)是常数,所以有:
PE ( pos + k , 2 i ) = PE ( pos , 2 i ) ⋅ u + PE ( pos , 2 i + 1 ) ⋅ v PE ( pos + k , 2 i + 1 ) = PE ( pos , 2 i + 1 ) ⋅ u − PE ( pos , 2 i ) ⋅ v \begin{aligned} \text{PE}(\text{pos} + k,2i) &= \text{PE}(\text{pos},2i) \cdot u + \text{PE}(\text{pos},2i+1)\cdot v\\ \text{PE}(\text{pos} + k,2i+1) &=\text{PE}(\text{pos},2i+1)\cdot u - \text{PE}(\text{pos},2i)\cdot v \end{aligned} PE(pos+k,2i)PE(pos+k,2i+1)=PE(pos,2i)⋅u+PE(pos,2i+1)⋅v=PE(pos,2i+1)⋅u−PE(pos,2i)⋅v
从这里就可以看出 PE ( pos + k , 2 i ) \text{PE}(\text{pos} + k,2i) PE(pos+k,2i)可以被 PE ( pos , 2 i ) \text{PE}(\text{pos},2i) PE(pos,2i)和 PE ( pos , 2 i + 1 ) \text{PE}(\text{pos},2i+1) PE(pos,2i+1)线性表示;同理 PE ( pos + k , 2 i + 1 ) \text{PE}(\text{pos} + k,2i+1) PE(pos+k,2i+1)也有类似的结果,所以 PE pos + k \text{PE}_{\text{pos} +k} PEpos+k可以被 PE pos \text{PE}_{\text{pos} } PEpos线性表示。
这也是为什么作者要交替使用正余弦函数,而不仅仅使用其中一个。
pos \text{pos} pos处的位置嵌入可以表示为:
PE pos = [ sin ( w 0 ⋅ pos ) cos ( w 0 ⋅ pos ) ⋮ sin ( w d 2 − 1 ⋅ pos ) cos ( w d 2 − 1 ⋅ pos ) ] \text{PE}_{\text{pos}} = \begin{bmatrix} \sin(w_0 \cdot \text{pos}) \\ \cos(w_0 \cdot \text{pos}) \\ \vdots \\ \sin(w_{\frac{d}{2} -1} \cdot \text{pos}) \\ \cos(w_{\frac{d}{2} -1} \cdot \text{pos}) \\ \end{bmatrix} PEpos= sin(w0⋅pos)cos(w0⋅pos)⋮sin(w2d−1⋅pos)cos(w2d−1⋅pos)
我们计算 PE pos + k \text{PE}_{\text{pos} +k} PEpos+k和 PE pos \text{PE}_{\text{pos}} PEpos的内积:
PE pos + k ⋅ PE pos = ∑ i = 0 d 2 − 1 [ sin ( w i ⋅ pos ) ⋅ sin ( w i ⋅ ( pos + k ) ) + cos ( w i ⋅ pos ) ⋅ cos ( w i ⋅ ( pos + k ) ) ] = ∑ i = 0 d 2 − 1 cos ( w i ⋅ pos − w i ⋅ ( pos + k ) ) = ∑ i = 0 d 2 − 1 cos ( w i ⋅ k ) \begin{aligned} \text{PE}_{\text{pos} +k} \cdot \text{PE}_{\text{pos}} &= \sum_{i=0}^{\frac{d}{2} -1} \left[ \sin(w_i \cdot \text{pos}) \cdot \sin(w_i \cdot (\text{pos} + k)) + \cos(w_i \cdot \text{pos}) \cdot \cos(w_i \cdot (\text{pos} + k)) \\ \right] \\ &= \sum_{i=0}^{\frac{d}{2} -1} \cos(w_i \cdot \text{pos} -w_i \cdot (\text{pos} + k) ) \\ &= \sum_{i=0}^{\frac{d}{2} -1} \cos(w_i \cdot k) \end{aligned} PEpos+k⋅PEpos=i=0∑2d−1[sin(wi⋅pos)⋅sin(wi⋅(pos+k))+cos(wi⋅pos)⋅cos(wi⋅(pos+k))]=i=0∑2d−1cos(wi⋅pos−wi⋅(pos+k))=i=0∑2d−1cos(wi⋅k)
其中利用了等式 cos ( x − y ) = sin ( x ) sin ( y ) + cos ( x ) cos ( y ) \cos(x-y) = \sin(x)\sin(y) + \cos(x) \cos(y) cos(x−y)=sin(x)sin(y)+cos(x)cos(y)。
参考文章4给出位置之间内积的关系:
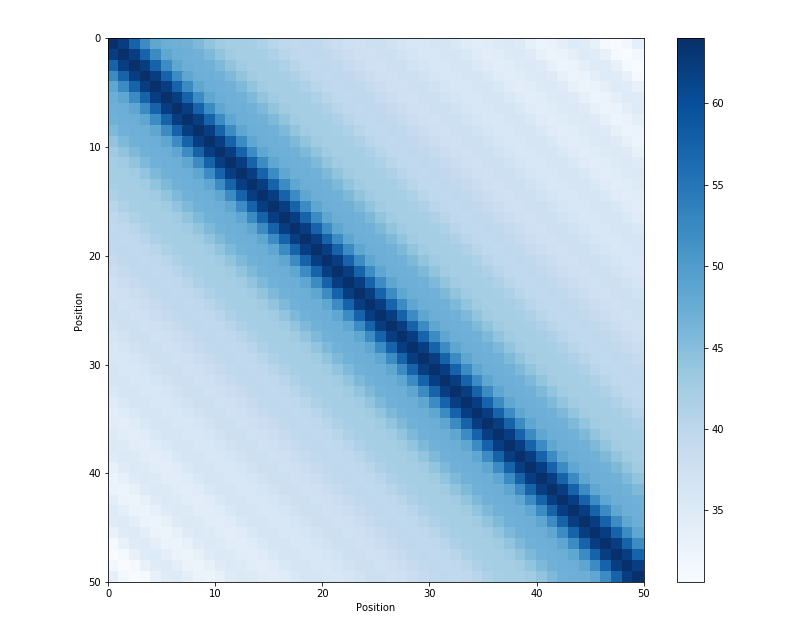
可以看到内积会随着相对位置的递增而减少,从而可以表示位置的相对距离。内积的结果是对称的,所以没有方向信息。
最后得到的位置编码需要和标记的词嵌入向量进行相加。
引用邱锡鹏老师关于问题为什么 Bert 的三个 Embedding 可以进行相加?的分析,来理解一下为什么可以相加。
文本可以看成是时序信号,一个时序的波可以用多个不同频率的正弦波叠加来表示,可能在神经网络中得到解耦,可能也不需要解耦。
不管怎么,我们为词嵌入赋予了位置信息。
下面先贴出代码实现:
class PositionalEncoding(nn.Module):def __init__(self, d_model: int = 512, dropout: float = 0.1, max_positions: int = 5000) -> None:super().__init__()self.dropout = nn.Dropout(p=dropout)# pe (max_positions, d_model)pe = torch.zeros(max_positions, d_model)# position (max_positions, 1)# create position columnposition = torch.arange(0, max_positions).unsqueeze(1)# div_term (d_model/2)# cauculate the divisor for positional encodingdiv_term = torch.exp(torch.arange(0, d_model, 2) * -(math.log(10000.0) / d_model))# calculate sine values on even indices# position * div_term will be broadcast to (max_positions, d_model/2)pe[:, 0::2] = torch.sin(position * div_term)# calculate cosine values on odd indicespe[:, 1::2] = torch.cos(position * div_term)# add a batch dimension: pe (1, max_positions, d_model)pe = pe.unsqueeze(0)# buffers will not be trainedself.register_buffer("pe", pe)def forward(self, x: Tensor) -> Tensor:"""Args:x (Tensor): (batch_size, seq_len, d_model) embeddingsReturns:Tensor: (batch_size, seq_len, d_model)"""# x.size(1) is the max sequence lengthx = x + self.pe[:, : x.size(1)]return self.dropout(x)
这里div_term是 pos 1000 0 2 i / d \frac{\text{pos}}{10000^{2i/d}} 100002i/dpos中的分母,假设 n = 10000 n=10000 n=10000有:
1 n 2 i / d = n − 2 i d = exp log ( n − 2 i d ) = exp − 2 i d log n = exp 2 i × − log n d \frac{1}{n^{2i/d}} = n^{-\frac{2i}{d}} = \exp^{\log (n^{-\frac{2i}{d}})} = \exp ^{-\frac{2i}{d}\log n } = \exp^{2i \times \frac{-\log n}{d}} n2i/d1=n−d2i=explog(n−d2i)=exp−d2ilogn=exp2i×d−logn
最后一项就是代码的实现形式,14行代码得到一个d_model/2维度的行向量;position被定义成一个max_len维度的列向量,position * div_term会被广播成(max_len, d_model/2)。
然后根据公式(1)和(2),分别为偶数和奇数维度赋值正余弦项;最后扩充pe的维度使得维度个数和输入一致。
最后通过register_buffer将计算出来的pe保存成模型的buffer而不是parameter,buffer的特点就是不需要更新。
多头注意力
自注意力
首先回顾下注意力机制,注意力机制允许模型为序列中不同的元素分配不同的权重。而自注意力中的"自"表示输入序列中的输入相互之间的注意力,即通过某种方式计算输入序列每个位置相互之间的相关性。
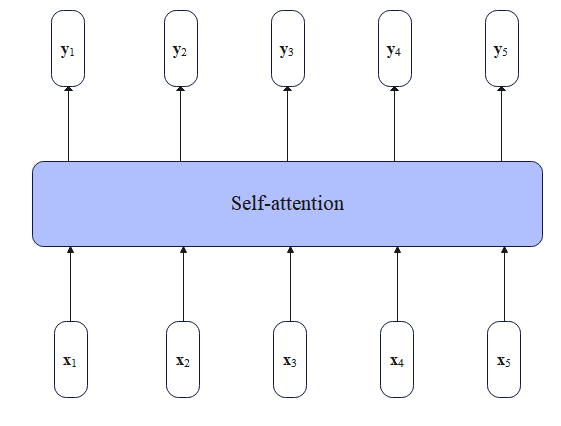
对于Transformer编码器来说,给定一个输入序列 ( x 1 , ⋯ , x n ) (\pmb x_1,\cdots,\pmb x_n) (x1,⋯,xn),这里假设 x i \pmb x_i xi是输入序列中第 i i i个位置所对应的词嵌入。自注意力产生了一个新的相同长度的嵌入 ( y 1 , ⋯ , y n ) (\pmb y_1,\cdots,\pmb y_n) (y1,⋯,yn),其中每个 y i \pmb y_i yi是所有的 x j \pmb x_j xj的加权和(包括 x i \pmb x_i xi本身):
y i = ∑ j α i j x j (5) \pmb y_i = \sum_j \alpha_{ij} \pmb x_j \tag 5 yi=j∑αijxj(5)
系数 α j i \alpha_{ji} αji被称为是注意力权重,且有性质 ∑ j α i j = 1 \sum_j \alpha_{ij} =1 ∑jαij=1。
缩放点积注意力
从文章注意力机制中我们知道有很多种计算注意力的方式,最高效的是点积注意力,即两个输入之间做点积。
以两个输入 x i , x j \pmb x_i,\pmb x_j xi,xj为例,它们之间的注意分数计算如下:
score ( x i , x j ) = x i ⋅ x j (6) \text{score}(\pmb x_i,\pmb x_j) = \pmb x_i \cdot \pmb x_j \tag{6} score(xi,xj)=xi⋅xj(6)
点积的结果是一个实数范围内的标量,结果越大代表两个向量越相似。这是计算两个输入之间的注意力分数,如果 x i \pmb x_i xi与所有的输入进行计算,就可以得到 n n n个注意力分数,为了转换为权重,经过Softmax归一化就可以得到权重向量 α \alpha α,其中 α i j \alpha_{ij} αij表示两个输入 i i i和 j j j之间的相关度(权重系数):
α i j = softmax ( score ( x i , x j ) ) = exp ( score ( x i , x j ) ) ∑ k = 1 n exp ( score ( x i , x k ) ) \begin{align} \alpha_{ij} &= \text{softmax}(\text{score}(\pmb x_i,\pmb x_j))\,\, \tag{7}\\ &= \frac{\exp(\text{score}(\pmb x_i,\pmb x_j))} { \sum_{k=1}^n \exp(\text{score}(\pmb x_i,\pmb x_k)) } \,\, \tag{8} \end{align} αij=softmax(score(xi,xj))=∑k=1nexp(score(xi,xk))exp(score(xi,xj))(7)(8)
得到了这些权重系数,就可以通过对所有的输入进行加权和得到输出 y i \pmb y_i yi,如公式 ( 5 ) (5) (5)所示。
这种计算注意力的方式和我们在seq2seq中遇到的不同,seq2seq是用解码器的隐状态与编码器所有时刻的输出计算,而自注意力是输入自己与自己进行计算。参与计算的只是输入本身。
但Transformer使用的是更加复杂一点的计算方式,来捕获更加丰富的信息。
在Transformer计算注意力的过程中,每个输入扮演了三种不同角色:
- Query: 与所有的输入进行比较,为当前关注的点。
- Key:作为与Query进行比较的角色,用于计算和Query之间的相关性。
- Value:用于计算当前注意力关注点的输出,根据注意力权重对不同的Value进行加权和。
为了生成这三种不同的角色,Transformer分别引入了三个权重矩阵 W Q , W K , W V W^Q,W^K,W^V WQ,WK,WV,分别将每个输入 x i \pmb x_i xi投影到不同角色query,key和value表示:
q i = x i W Q ; k i = x i W K ; v i = x i W V (9) \pmb q_i = \pmb x_iW^Q;\quad \pmb k_i = \pmb x_i W^K; \quad \pmb v_i = \pmb x_iW^V \tag{9} qi=xiWQ;ki=xiWK;vi=xiWV(9)
如果把注意力过程类比成搜索的话,那么假设在百度中输入"自然语言处理是什么",那么Query就是这个搜索的语句;Key相当于检索到的网页的标题;Value就是网页的内容。
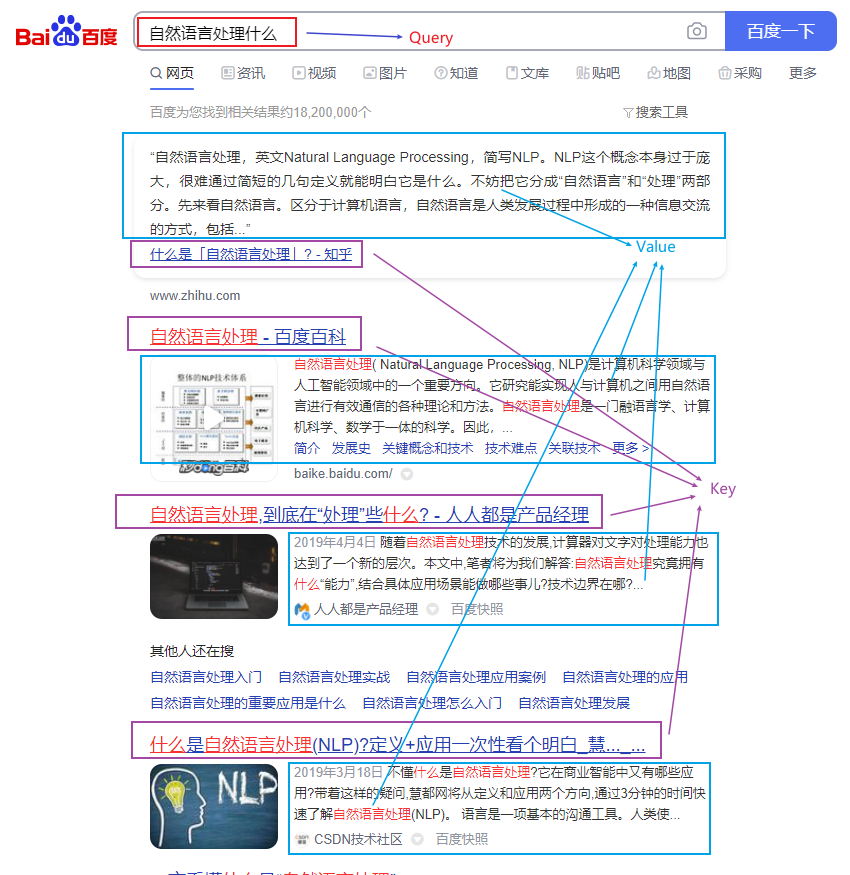
Query和Key是用于比较的,Value是用于提取特征的。通过将输入映射到不同的角色,使模型具有更强的学习能力。
由于key和query向量需要计算点积,因此它们的维度一定是一致的,记为 d k d_k dk;而value的维度可以和它们不一样,记为 d v d_v dv。假设词嵌入向量的维度为 d m o d e l d_{model} dmodel,为了方便,这里简记为 d d d。
那么我们就可以得到投影矩阵的维度, W Q ∈ R d × d k , W K ∈ R d × d k , W V ∈ R d × d v W^Q \in \Bbb R^{d \times d_k},W^K \in \Bbb R^{d \times d_k},W^V \in \Bbb R^{d \times d_v} WQ∈Rd×dk,WK∈Rd×dk,WV∈Rd×dv。
注意Transformer中的每个输入 x \pmb x x和输出 y \pmb y y的维度都是 1 × d 1 \times d 1×d,如果考虑批次和序列长度的话,完整维度是(batch_size, seq_len, embed_dim)。我们这里先考虑单个输入,即维度为 1 × d 1 \times d 1×d的 x i \pmb x_i xi。
现在我们用公式 ( 9 ) (9) (9)把所有的输入投影到key,query,value向量表示,对应的维度为 1 × d k , 1 × d k , 1 × d v 1\times d_k,1 \times d_k, 1\times d_v 1×dk,1×dk,1×dv。然后我们假设用 x i \pmb x_i xi的query向量 q i \pmb q_i qi和 x j \pmb x_j xj的key向量 k j \pmb k_j kj来计算点积,因为它们的维度都是 1 × d k 1 \times d_k 1×dk,所以可以计算点积,我们得到新的注意力分数计算函数:
score ( x i , x j ) = q i ⋅ k j (10) \text{score}(\pmb x_i,\pmb x_j) = \pmb q_i \cdot \pmb k_j \tag{10} score(xi,xj)=qi⋅kj(10)
也可以表示为 q i k j T \pmb q_i \pmb k_j^T qikjT,点积的结果是一个标量,但这个结果可能非常大(不管是正的还是负的),这会使得softmax函数值进入一个导数非常小的区域。需要对这个注意力得分进行缩放,缩放使得分布更加平滑。一种缩放的方法是把点积结果除以一个和嵌入大小相关的因子(factor)。注意这是在传递给softmax之前进行的。
Transformer的做法是除以query和key向量维度 d k d_k dk的平方根:
score ( x i , x j ) = q i ⋅ k j d k (11) \text{score}(\pmb x_i,\pmb x_j) = \frac{\pmb q_i\cdot \pmb k_j}{\sqrt{d_k}} \tag {11} score(xi,xj)=dkqi⋅kj(11)
计算权重系数 α \alpha α的过程和上面介绍的一样(公式 ( 7 ) − ( 8 ) (7)-(8) (7)−(8)),但在计算输出 y i \pmb y_i yi时的加权和变成了基于value向量 v \pmb v v:
y i = ∑ j α i j v j (12) \pmb y_i = \sum_{j} \alpha_{ij} \pmb v_j \tag{12} yi=j∑αijvj(12)
整个计算过程可以利用矩阵乘法一次计算,首先通过将具有 N N N个token的输入序列映射到一个(嵌入)矩阵 X ∈ R N × d X \in \Bbb R^{N \times d} X∈RN×d。然后让 X X X乘到key,query和value权重矩阵( W Q , W K , W V W^Q,W^K,W^V WQ,WK,WV,注意它们的维度)上,得到矩阵 Q ∈ R N × d k , K ∈ R N × d k , V ∈ R N × d v Q \in \Bbb R^{N \times d_k},K \in \Bbb R^{N \times d_k},V \in \Bbb R^{N \times d_v} Q∈RN×dk,K∈RN×dk,V∈RN×dv,其中包含所有输入的key,query和value向量:
Q = X W Q ; K = X W K ; V = X W V (13) Q=XW^Q;\quad K=XW^K;\quad V=XW^V \tag{13} Q=XWQ;K=XWK;V=XWV(13)
这样我们一次性计算出了所有的 Q , K , V Q,K,V Q,K,V,然后通过矩阵乘法 Q K T QK^T QKT得到相似度得分矩阵,形状为 N × N N \times N N×N。接着缩放这个得分矩阵,进行Softmax得到权重矩阵。最后拿权重矩阵去乘 V V V就可以得到一个形状为 N × d v N \times d_v N×dv的矩阵,这就是经过注意力之后的结果,表示每个输入的自注意力后的向量表示。
上面说了这么多,实际可以用一个公式表示:
SelfAttention ( Q , K , V ) = softmax ( Q K T d k ) V (14) \text{SelfAttention} (Q,K,V) = \text{softmax}\left(\frac{QK^T}{\sqrt {d_k}}\right) V \tag{14} SelfAttention(Q,K,V)=softmax(dkQKT)V(14)
我们前面不是说,注意力层计算的结果 y \pmb y y和输入 x \pmb x x的维度是一致的吗?但这里为什么输出的维度是 d v d_v dv,而不是词嵌入维度 d d d呢?因为Encoder Layer除了自注意力层还包含一个FF层,它就是用于将维度转换会 d v d_v dv的,我们后面再深入探讨,前面那么说是为了让大家更好地理解。所以,准确地说应该是Transformer Block的输入和输出的维度是一致的。
为了更好地理解,下面举一个例子,这个例子来自文章The Illustrated Transformer。假设输入包含两个单词"Thinking Machines"。
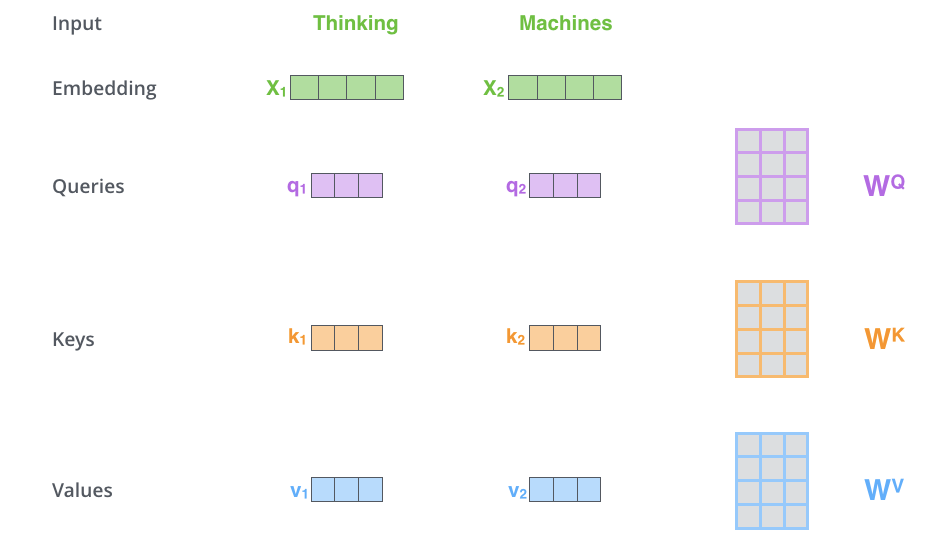
计算自注意力的第一步就是,为编码器层的每个输入,都创建三个向量,分别是query向量,key向量和value向量。
正如我们上面所说,每个向量都是乘上一个权重矩阵得到的,这些权重矩阵是随模型一起训练的。
进行线性映射的目的是转换向量的维度,转换成一个更小的维度。原文中是将 512 512 512维转换为 64 64 64维。
比如输入 x 1 x_1 x1乘以矩阵 W Q W^Q WQ得到query向量 q 1 q_1 q1,然后乘以 W k W^k Wk和 W V W^V WV分别得到key向量 k 1 k_1 k1和value向量 v 1 v_1 v1。
第二步 是计算注意力得分,假设我们想计算单词“Thinking”的注意力得分,我们需要对输入序列中的所有单词(包括自身)都进行某个操作。得到单词“Thinking”对于输入序列中每个单词的注意力得分,如果某个位置的得分越大,那么在生成编码时就越需要考虑这个位置。或者说注意力就是衡量 q q q和 k k k的相关性,相关性越大,那么在得到最终输出时, k k k对应的 v v v在生成输出时贡献也越大。
那么这里所说的操作是什么呢?其实很简单,就是点乘。表示两个向量在多大程度上指向同一方向。类似余弦相似度,除了没有对向量的模进行归一化。
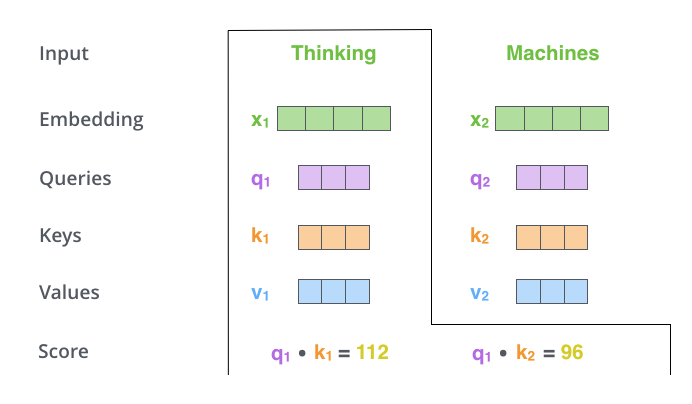
所以如果我们计算单词“Thinking”的注意力得分,需要计算 q 1 q_1 q1对 k 1 k_1 k1和 k 2 k_2 k2的点积。如上图所示。
第三步和第四步 是进行进行缩放,然后经过softmax函数,使得每个得分都是正的,且总和为 1 1 1。
经过Softmax之后的值就可以看成是一个权重了,也称为注意力权重。决定每个单词在生成这个位置的编码时能够共享多大程度。
第五步 用每个单词的value向量乘上对应的注意力权重。这一步用于保存我们想要注意单词的信息(给定一个很大的权重),而抑制我们不关心的单词信息(给定一个很小的权重)。
第六步 累加第五步的结果,得到一个新的向量,也就是自注意力层在这个位置(这里是对于第一个单词“Thinking”来说)的输出。举一个极端的例子,假设某个单词的权重非常大,比如是 1 1 1,其他单词都是 0 0 0,那么这一步的输出就是该单词对应的value向量。
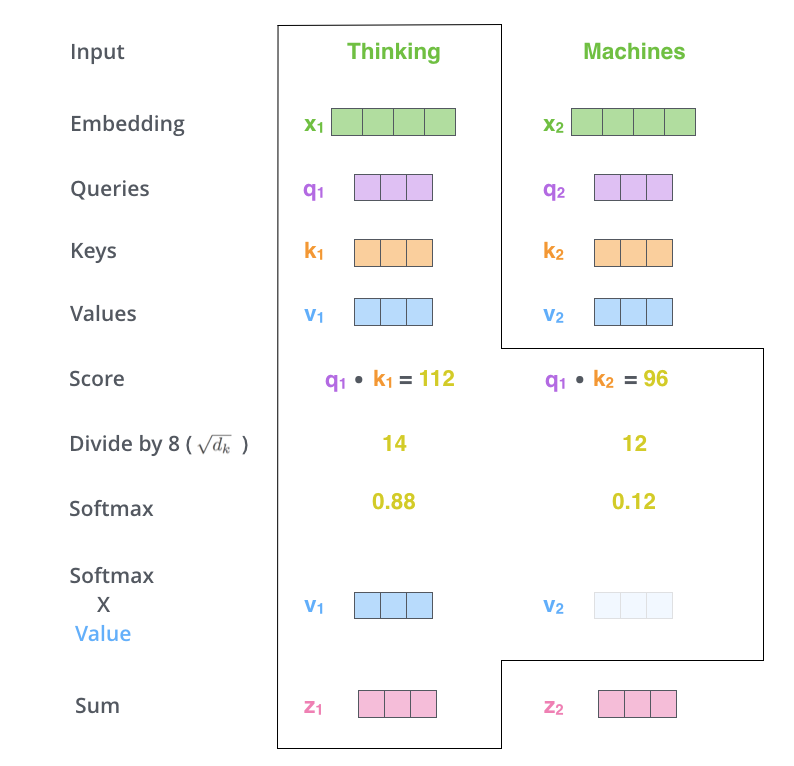
这就是计算第一个单词的自注意力输出完整过程。自注意力层的魅力在于,计算所有单词的输出可以通过矩阵运算一次完成。
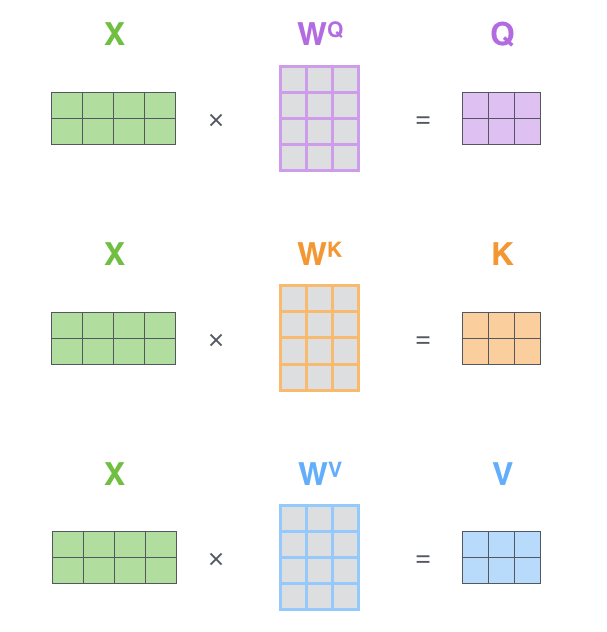
我们把所有的输入编入一个矩阵 X X X,上面的例子有两个输入,所以这里的 X X X矩阵有两行。分别乘上权重矩阵 W Q , W K , W V W^Q,W^K,W^V WQ,WK,WV就得到了 Q , K , V Q,K,V Q,K,V向量矩阵。
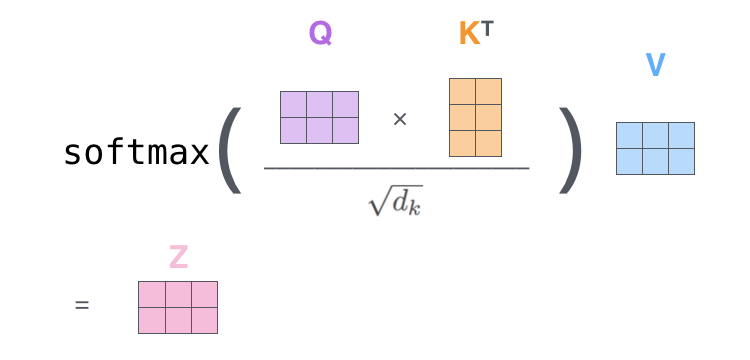
然后除以 d k \sqrt{d_k} dk进行缩放,再经过Softmax,得到注意力权重矩阵,接着乘以value向量矩阵 V V V,就一次得到了所有单词的输出矩阵 Z Z Z。上图就是公式 ( 14 ) (14) (14)。
注意权重矩阵 W Q , W K , W V W^Q,W^K,W^V WQ,WK,WV都是可以训练的,因此通过训练,可以为每个输入单词生成不同的注意力得分,从而得到不同的输出。
多头注意力
上面介绍的缩放点积注意力把原始的 x \pmb x x映射到不同的空间后,去做注意力。每次映射相当于是在特定空间中去建模特定的语义交互关系,类似卷积中的多通道可以得到多个特征图,那么多个注意力可以得到多个不同方面的语义交互关系。可以让模型更好地关注到不同位置的信息,捕捉到输入序列中不同依赖关系和语义信息。有助于处理长序列、解决语义消歧、句子表示等任务,提高模型的建模能力。
对于每个头 i i i,都有它自己不同的key,query和value矩阵: W i K , W i Q , W i V W_i^K,W_i^Q,W_i^V WiK,WiQ,WiV。在多头注意力中,key和query的维度是 d k d_k dk,value嵌入的维度是 d v d_v dv,这样每个头 i i i,权重 W i Q ∈ R d × d k , W i K ∈ R d × d k , W i V ∈ R d × d v W_i^Q \in \Bbb R^{d \times d_k},W_i^K \in \Bbb R^{d \times d_k},W_i^V \in \Bbb R^{d \times d_v} WiQ∈Rd×dk,WiK∈Rd×dk,WiV∈Rd×dv,然后与压缩到 X X X中的输入相乘,得到 Q ∈ R N × d k , K ∈ R N × d k , V ∈ R N × d v Q \in \Bbb R^{N \times d_k},K \in \Bbb R^{N \times d_k},V \in \Bbb R^{N \times d_v} Q∈RN×dk,K∈RN×dk,V∈RN×dv。
得到这些多头注意力的组合以后,再把它们拼接起来,然后通过一个线性变化映射回原来的维度,保证输入和输出的维度一致。
h个头的输出是 N × d v N \times d_v N×dv的向量,接着这些输出被组合到一起压缩成原来的维度 d d d,这是拼接每个头的输出然后经过另一个线性投影 W O ∈ R h d v × d W^O \in \Bbb R^{hd_v \times d} WO∈Rhdv×d实现的,压缩到原来每个token的输出维度,或共 N × d N \times d N×d个输出:
MultiHeadAttention ( X ) = ( head 1 ⊕ head 2 ⋯ ⊕ head h ) W O (15) \text{MultiHeadAttention}(X) = (\text{head}_1 \oplus \text{head}_2 \cdots \oplus \text{head}_h) W^O \tag{15} MultiHeadAttention(X)=(head1⊕head2⋯⊕headh)WO(15)
head i = SelfAttention ( Q , K , V ) (16) \text{head}_i = \text{SelfAttention}(Q,K,V) \tag{16} headi=SelfAttention(Q,K,V)(16)
Q = X W i Q ; K = X W i K ; V = X W i V (17) Q=XW^Q_i; \,\, K=XW_i^K;\,\, V=XW_i^V \tag{17} Q=XWiQ;K=XWiK;V=XWiV(17)
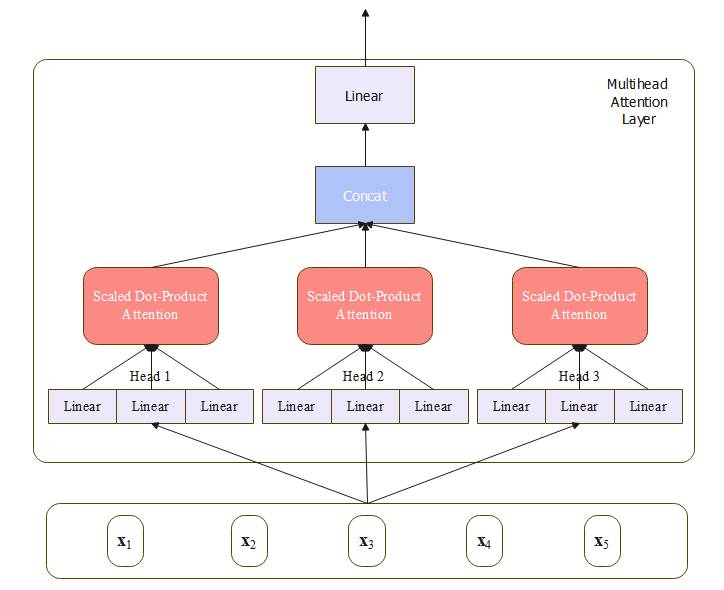
上图是一个三个头的注意力示意图,在原论文中, d = 512 d=512 d=512,有 h = 8 h=8 h=8个注意力头。每个头中的 d k = d v = d / h = 64 d_k=d_v=d/h=64 dk=dv=d/h=64,由于每个头维度的减少,总的计算量和正常维度的单头注意力一样( 8 × 64 = 512 8 \times 64 =512 8×64=512)。
class MultiHeadAttention(nn.Module):def __init__(self,d_model: int = 512,n_heads: int = 8,dropout: float = 0.1,) -> None:"""Args:d_model (int, optional): dimension of embeddings. Defaults to 512.n_heads (int, optional): numer of self attention heads. Defaults to 8.dropout (float, optional): dropout ratio. Defaults to 0.1."""super().__init__()assert d_model % n_heads == 0self.d_model = d_modelself.n_heads = n_headsself.d_key = d_model // n_heads # dimension of every headself.q = nn.Linear(d_model, d_model) # query matrixself.k = nn.Linear(d_model, d_model) # key matrixself.v = nn.Linear(d_model, d_model) # value matrixself.concat = nn.Linear(d_model, d_model) # outputself.dropout = nn.Dropout(dropout)def split_heads(self, x: Tensor, is_key: bool = False) -> Tensor:batch_size = x.size(0)# x (batch_size, seq_len, n_heads, d_key)x = x.view(batch_size, -1, self.n_heads, self.d_key)if is_key:# (batch_size, n_heads, d_key, seq_len)return x.permute(0, 2, 3, 1)# (batch_size, n_heads, seq_len, d_key)return x.transpose(1, 2)def merge_heads(self, x: Tensor) -> Tensor:x = x.transpose(1, 2).contiguous().view(x.size(0), -1, self.d_model)return xdef attenion(self,query: Tensor,key: Tensor,value: Tensor,mask: Tensor = None,keep_attentions: bool = False,):scores = torch.matmul(query, key) / math.sqrt(self.d_key)if mask is not None:# Fill those positions of product as -1e9 where mask positions are 0, because exp(-1e9) will get zero.# Note that we cannot set it to negative infinity, as there may be a situation where negative infinity is divided by negative infinity.scores = scores.masked_fill(mask == 0, -1e9)# weights (batch_size, n_heads, q_length, k_length)weights = self.dropout(torch.softmax(scores, dim=-1))# (batch_size, n_heads, q_length, k_length) x (batch_size, n_heads, v_length, d_key) -> (batch_size, n_heads, q_length, d_key)# assert k_length == v_length# attn_output (batch_size, n_heads, q_length, d_key)attn_output = torch.matmul(weights, value)if keep_attentions:self.weights = weightselse:del weightsreturn attn_outputdef forward(self,query: Tensor,key: Tensor,value: Tensor,mask: Tensor = None,keep_attentions: bool = False,) -> Tuple[Tensor, Tensor]:"""Args:query (Tensor): (batch_size, q_length, d_model)key (Tensor): (batch_size, k_length, d_model)value (Tensor): (batch_size, v_length, d_model)mask (Tensor, optional): mask for padding or decoder. Defaults to None.keep_attentions (bool): whether keep attention weigths or not. Defaults to False.Returns:output (Tensor): (batch_size, q_length, d_model) attention output"""query, key, value = self.q(query), self.k(key), self.v(value)query, key, value = (self.split_heads(query),self.split_heads(key, is_key=True),self.split_heads(value),)attn_output = self.attenion(query, key, value, mask, keep_attentions)del querydel keydel value# Concatconcat_output = self.merge_heads(attn_output)# the final liear# output (batch_size, q_length, d_model)output = self.concat(concat_output)return output在forward()中,首先利用三个线性变换分别计算query,key,value矩阵(后续文章GPT实现中可以看到这个三个线性编变换也可以合并成一个)。接着拆分成多个头,传给attention()计算多头注意力,通过keep_attentions参数可以指定是否保存注意力权重,后续可以进行观察。然后合并多头注意力的结果。最后经过一个用作拼接的线性层。
注意力这里的拆分和合并其实都是reshape操作,在代码的最后删除掉不需要的引用,以帮助GC释放GPU缓存。
![[排序算法] 如何解决快速排序效率低的问题------三路划分](https://img-blog.csdnimg.cn/direct/c5aafbe58f214f3ead0aea4843e5e8f6.png)