岭回归也是一种用于回归的线性模型,它的预测公式与线性回归相同,但是在岭回归里,对于系数的选择不仅要在训练数据上得到好的预测结果,而且还要拟合附加约束,还希望系数尽量小,这意味着每个特征对输出的影响应该尽可能小,同时仍给出很好的预测结果。这种约束是所谓的正则化的一个例子。
正则化是指对模型做显式约束,用来避免过拟合。岭回归用到的这种被成为L2正则化。
用波士顿房价数据集为例:
import mglearn.datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import RidgeX,y=mglearn.datasets.load_extended_boston()
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=0
)ridge=Ridge().fit(X_train,y_train)
print('训练集score:{:.2f}'.format(ridge.score(X_train,y_train)))
print('测试集score:{:.2f}'.format(ridge.score(X_test,y_test)))
可以看到Ridge(岭回归)在训练集上的分数要小于线性回归,但是在测试集上的分数要更高。因为线性回归对数据存在过拟合,而岭回归是一种约束更强的模型,所以更不容易过拟合。
复杂度更小的模型意味着在训练集上的性能差,但是泛化性能更好,由于更多的需求场景是对泛化性能更感兴趣,所以应该选择岭回归而非线性回归。
岭回归模型可以在模型的简单性和训练集性能之间做出权衡,通过alpha系数来调整。alpha系数默认为1,增大alpha会降低训练集性能,但可能会提高泛化性能。
import mglearn.datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import RidgeX,y=mglearn.datasets.load_extended_boston()
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=0
)ridge_10=Ridge(alpha=10).fit(X_train,y_train)
print('训练集score:{:.2f}'.format(ridge_10.score(X_train,y_train)))
print('测试集score:{:.2f}'.format(ridge_10.score(X_test,y_test)))

相反的,如果减小alpha会让系数收到的限制更小,更接近于线性回归模型。
通过查看alpha不同取值时的coef_属性,定性的理解alpha参数是如何改变模型的:
import mglearn.datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Ridge,LinearRegression
from sklearn.neighbors import KNeighborsRegressor
import matplotlib.pyplot as plt
import numpy as npplt.rcParams['font.sans-serif']=['SimHei']X,y=mglearn.datasets.load_extended_boston()
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=0
)
ridge=Ridge().fit(X_train,y_train)
ridge_10=Ridge(alpha=10).fit(X_train,y_train)
ridge_01=Ridge(alpha=0.1).fit(X_train,y_train)
lr=LinearRegression().fit(X_train,y_train)plt.plot(ridge.coef_,'s',label='岭 alpha=1')
plt.plot(ridge_10.coef_,'^',label='岭 alpha=10')
plt.plot(ridge_01.coef_,'v',label='岭 alpha=0.1')plt.plot(lr.coef_,'o',label='线性回归')
plt.xlabel('index')
plt.ylabel('大小')
plt.hlines(0,0,len(lr.coef_))
plt.ylim(-25,25)
plt.legend()
plt.show()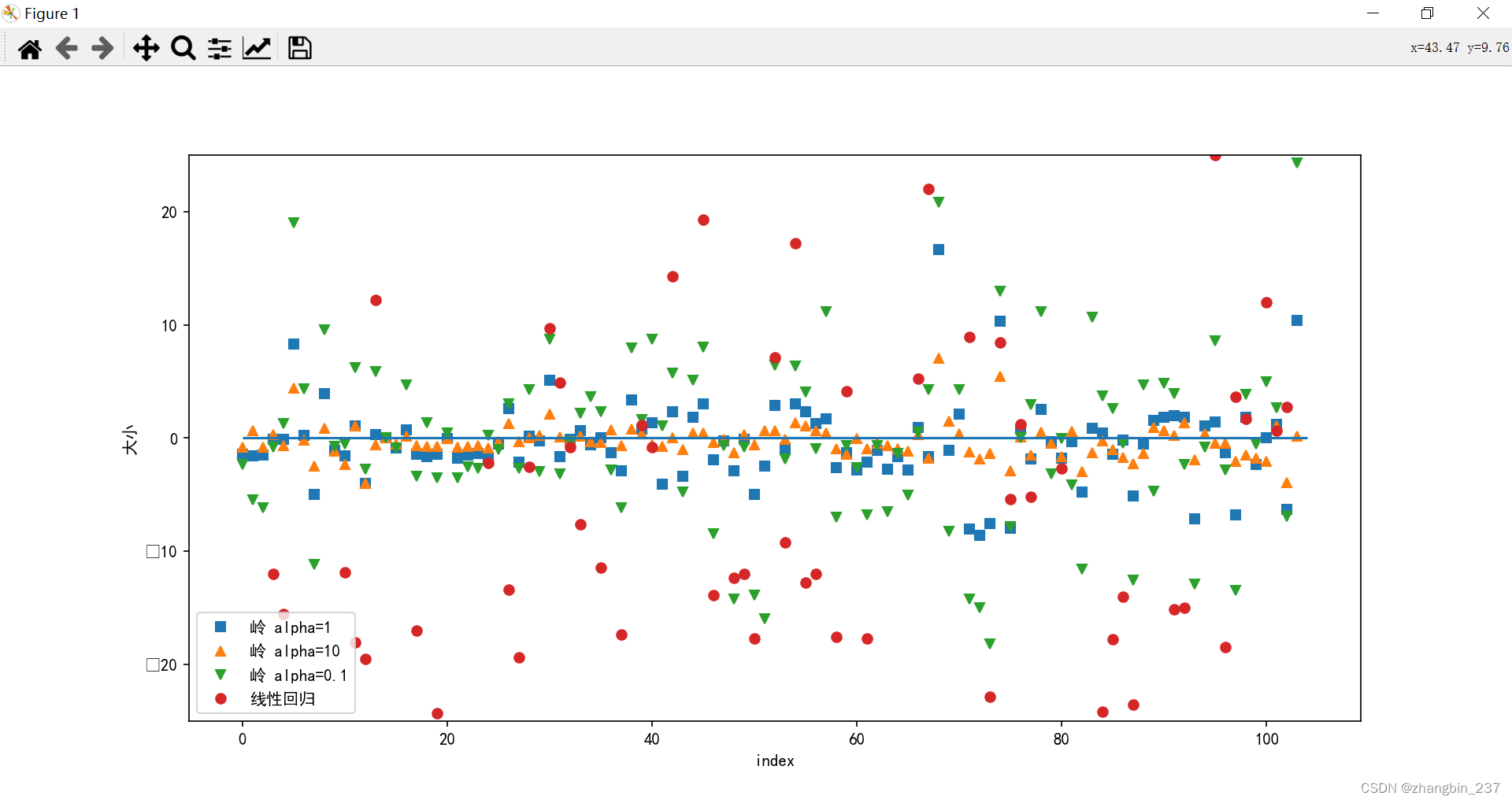
图中X轴对应coef_元素:x=0对应第一个特征的系数,x=1对应第二个,以此类推。
可以看到,alpha取10时,系数大小大多在-3到3之间,alpha=1的模型,系数范围更大一些,alpha=0.1时,系数点的范围就很大了。