数学界一直在干一件令人恶心的丑事:明明我求的是Σ1/708249541360742487,它给的答案却是ln708249541360742487+0.5772156649(欧拉常数,通常以C表示),门外汉皆以为Σ1/n→∞是正经结论,全然不知它无关Σ1/n,而是“lnn+0.5772156649…”在顶缸,如今的电脑编程及其它各种数学对Σ1/n进行的运算、挂着是Σ1/n的羊头、卖的全是lnn+C狗肉,严谨的数学界骗局能如此畅行,是因为张冠李戴、偷梁换柱在纯粹数学大家庭习以为常。
Σ1/n求和卖的一直是lnn+C的狗肉
Σ1/n=lnn+C是纯粹数学的著名公式,它是欧洲数学家欧拉创造的。欧拉采用的方法是:将Σ1/n与lnn对应“持续翻倍”,得到:Σ1/n=1+(1/2+1/3)+(1/4+1/5+1/6+1/7)+…+[1/2^k~1/(2^k-1)]=1+0.8333…+0.7595…+…+0.6931…=0.5772156649…+ln2*k;lnn=ln2+ln2+ln2+…+ln2+…=ln2*k,在欧拉眼里,k>10以后,“1/2^k~1/(2^k-1)”之和与ln2并轨,他将无限Σ1/n变成了无限lnn、除了开始的几百个1/n项是实算,其余的Σ1/n都替换为lnn,也就是说“欧拉常数”是赤裸裸的偷梁换柱!
欧拉常数源于欧拉的偷梁换柱
如果一个人的智商正常,看到“Σ1/n=lnn+C”的第一眼就知道它不成立,因为Σ1/n与lnn是风马牛不相及的两个变量,彼此的趋势是“相互趋近”,而Σ1/n=lnn+C则是“把Σ1/n平移C变成了lnn”,这是明目张胆的胡作非为;趋势不可改变,相互趋近的变量必定相交,这是规律、是没有任何力量能够改变的自然规律!只需动动笔,就会发现1/n的曲率大过ln(1+1/n)、Σ1/n=1+1/2+1/3+…+1/n+…”的收敛速度大过“lnn=ln(1+1)+ln(1+1/2)+ln(1+1/3)+…+ln(1+1/n)+…”,这意味着lnn会上穿Σ1/n——彼此一定相交。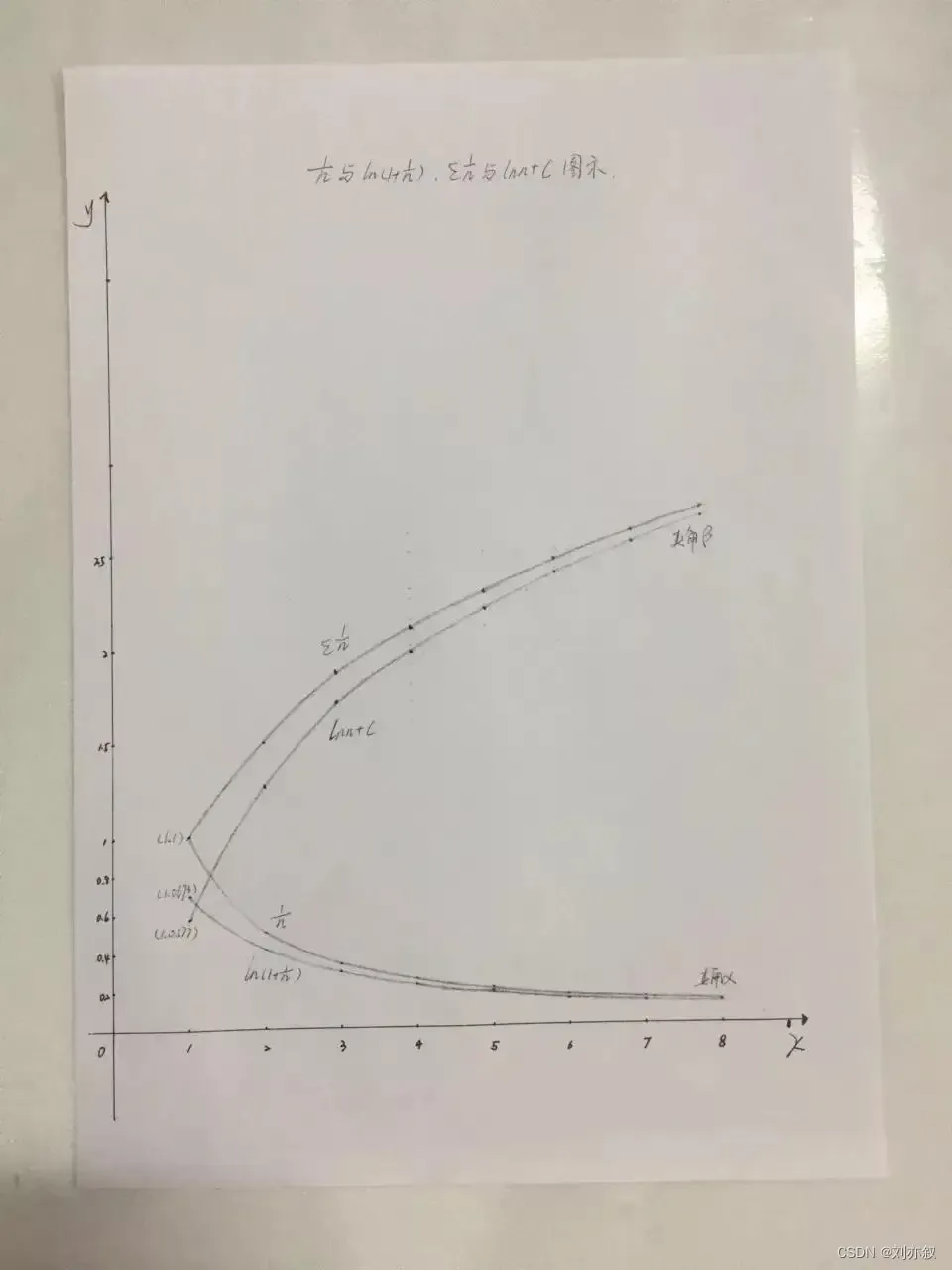
1/n与ln(1+1/n)、Σ1/n与lnn+C必定相交
欧拉无视趋势,把毫不相干的Σ1/n与lnn视为平移函数(间距为常数C即“平行线”),他这是拿观众当白 痴!诡异的是数学界面对着欧拉的胡言乱语真的就成了白 痴,不仅没有人指责欧拉吃相难看,反而对着他的鬼话丑态百出唱赞歌。
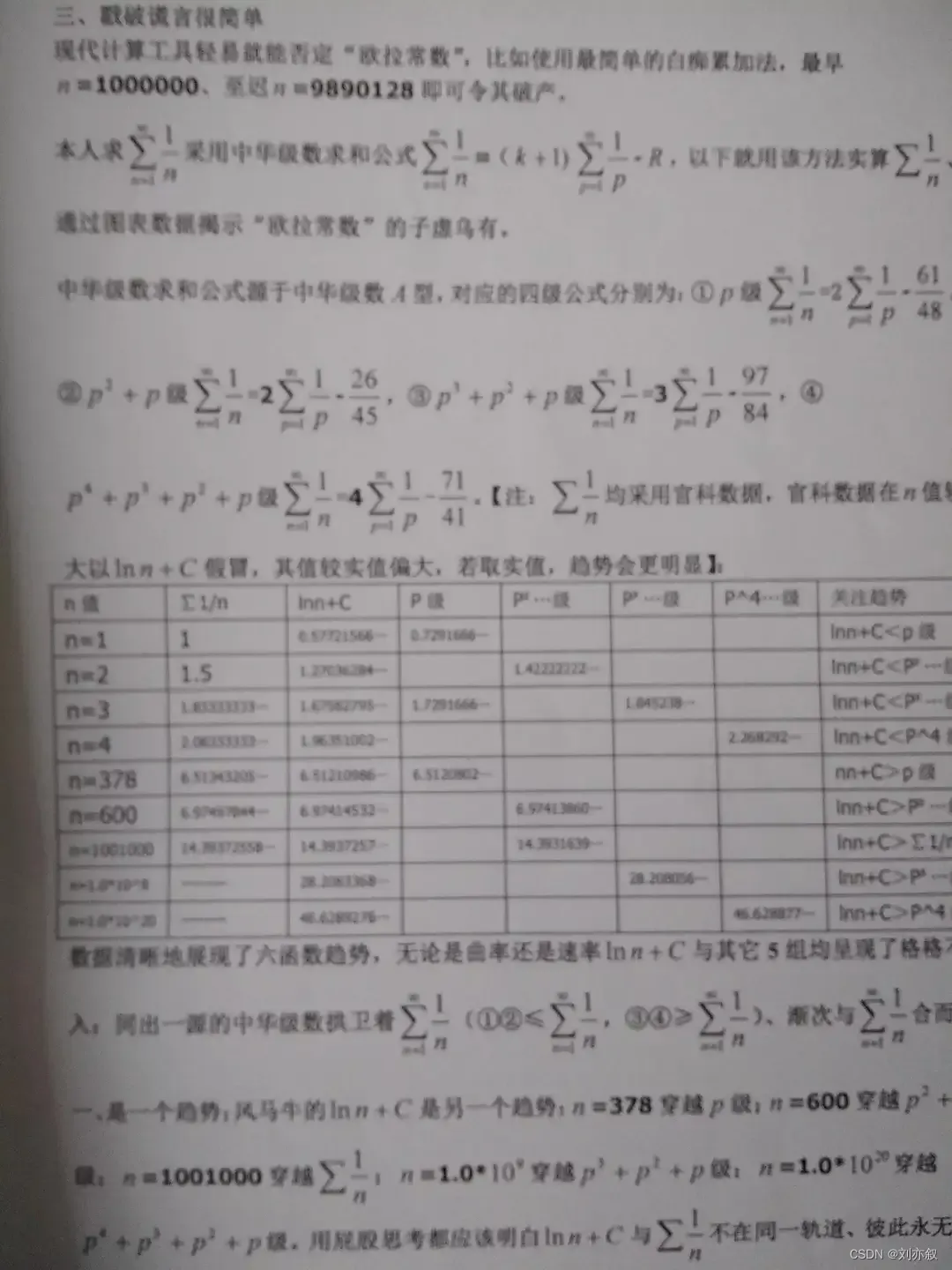
现代计算工具很容易就能否定欧拉常数,使用最简单的硬算法,Σ1/n与lnn+C的交点位于n=1000000~9890128之间。既然数学人都在说计算机功能强大,那么请计算这个小数值,验证我和欧拉哪个在说假话。
“Σ1/n=(k+1)Σ1/p-R”是我利用中华级数A型发现的解决Σ1/n求和方案,该公式有四级,每一级都可以轻松获得Σ1/n的确值或约值,比数学界目前采用的任何方法都直观精确,中华级数求和公式的四级曲率和速率都与1/n极度吻合,而lnn的曲率和速率与1/n却截然相反(如图)
中华级数求和公式实证欧拉常数荒谬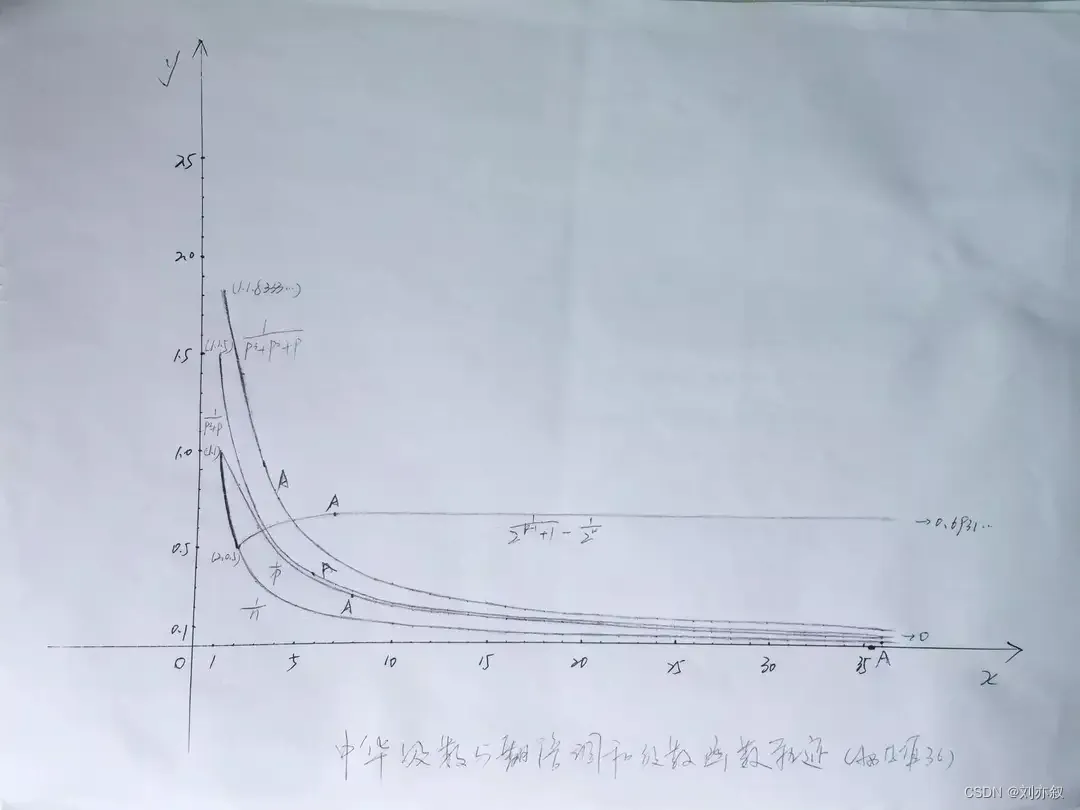
中华级数A型四级曲率与速率
此外还有一些数理常识可以证明欧拉在胡作非为。①.反证法。数理知识和趋势理论殊途同归:1/n→0,ln(1+1/n)→常数,这个前提若能推得Σ1/n>lnn=lnn+C,结论只能是“0>常数”,显然这不可能。②.Σ1/n是无限递缩级数,让它变成无限常量级数伤天害理。③.Σ1/n的任意分级(有通项的分级)都能得到收敛确值,依据“子集收敛则级数收敛”定理可证Σ1/n收敛。④.欧拉毫无理由地用lnn的翻倍级数绑架Σ1/n“翻倍求和”犯了常识性错误:lnn是ln(1+1/n)的无限积分,Σ1/n是1/n的无穷累加,lnn的无限积分是无限ln2,Σ1/n的无穷累加如何会是0.5772156649…+无限ln2?用脚指头都能掰扯明白Σ1/n与ln2不存在瓜葛、也就绝无可能产生任何关联。
“数学是严谨的”是数学人的口头禅座右铭,但面对以不严谨著称的欧拉,数学人总是听之任之故意装糊涂。欧拉知道有理数Σ1/n与无理数lnn毫不相关,彼此拉不上关系更画不上等号,但不严谨的数学习惯和急功近利的学术心理让他把表象当真相,以他命名的恒等式、定理都是这样获得的。

欧拉在中国数学界地位畸高
无论从维护教主、尊重信仰高度,还是尊重学问、对自己智商负责角度,数学人都应该站出来重新认识欧拉,这有助于破除权威迷信、认清欧拉浮皮潦草的歪理和结论给数学造成了多少混乱。
我在此向全世界呐喊:趋势理论证明Σ1/n与lnn必然相交!Σ1/n与lnn之间不可能存在常数!Σ1/n=lnn+C是伪命题!“欧拉常数”是弥天大谎!