C语言程序设计——数学运算-编程知识

基本运算符

运算符	说明	例子
=	赋值运算符	a = b;
+、-、*、/、()	基本四则运算	a = (a + c) * d;
%	取余运算符	a = b % 2
&、^、~、l	位运算	a = ~b l c
>>、<<	左移和右移	a = b >> 2

在c语言的数学运算中，所涉及到的符号如图所示，在使用过程中应该了解的就是各个符号在同一条语句中的优先级，以及在现实中很少用到的取余运算符的作用。

位运算

个人认为对于位运算的理解很大程度上能够帮助理解计算机的逻辑，所以单独讲一下，以及相关符号的使用。

在计算机中，所有的命令都是0、1来表示的，它代表的是两种情况。我们传输数据是通过电信号来传播的，那么高电平代表1，低电平代表0。从物理上来讲这是最容易实现的传输方式。我印象中在高中物理中也有过类似的扩展，开关的"打开"与"闭合两种状态"，假如说有8盏灯来传递我们的信号，那么根据特定排列方式，选择我们需要传递的数字，按照这个数字闭合和打开开关就好了。
全闭合状态是0000 0000
如果我们想要传递一个13，以二进制的传递的话就是0000 1101。只需要闭合这三盏灯的开关，使其亮起，我们就可以接收到传递的信号是13.计算机内部同理。

二进制与十进制

以125为例子
十进制： $1 * 10^2 +2*10^1+5*10^0$
二进制： $1*2^6 + 1 * 2^5 +1*2^4+1*2^3+1*2^2+0*2^1+1*2^0 =64+32+16+8+4+1$
其中十进制的10与二进制中的2叫做位权，那么不同进制间的转换就是位权的变换，他们本身的数值不会发生转换。如果不熟练，就找几个数字多练习几次就很好理解了。

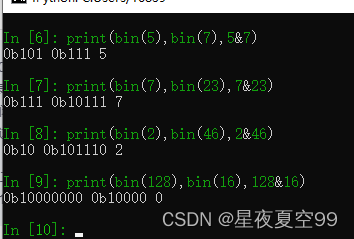
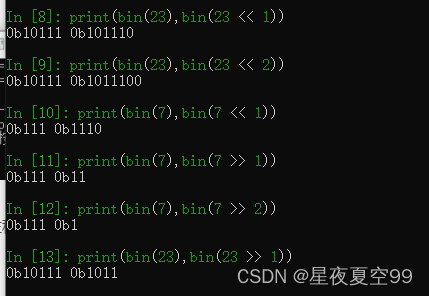
与运算：当进行位运算时，都为1时，结果才为1，出现0结果则为0。就好像我们是同一根电线上的两个开关，只有当我们都闭合的时候，才能通电，一个是打开状态都不可以。在位运算当中，每一个开关都只与自己所处电线的开关进行计算(如下图)。

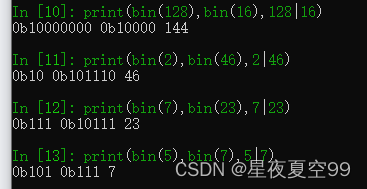
在第一个例子中5=>101，7=>111。按位进行与运算，两个二进制数中，5的第二位是0所以最后结果也就是101也就是5。
第二个例子中，7=>111，23=>10111。发现23的二进制位要多于7，这个情况下就在111前面补0，然后进行按位与运算

或运算：与运算你与我都为1结果为1，那么或就是你或我为1，结果就为1.与运算就相当于串联，或运算就相当于并联。
在这里插入图片描述
非运算：可以理解为按位取相反，0的位变成1，1的位变成0。在之前的循环读入中已经接触过了。但是需要一提的是，要注意数据类型的位数，同时在取反的时候符号位也会取反。这里没有把全部位都显示出来。
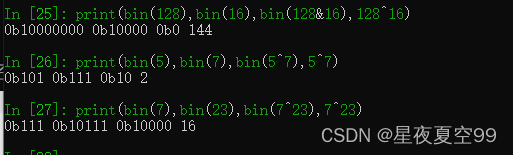
在这里插入图片描述

异或运算：

异或可以理解为理解为一种逆运算，就像a + b = c,那么b = c - a。异或的运算方式为相同为0，不同为1，为什么他是逆运算呢，5^7 = 2, 2^5 = 7,2^7 = 5。也就是两个数异或之后得出来的数，再与原任意一个数异或可以得出另外一个数字。

小练习

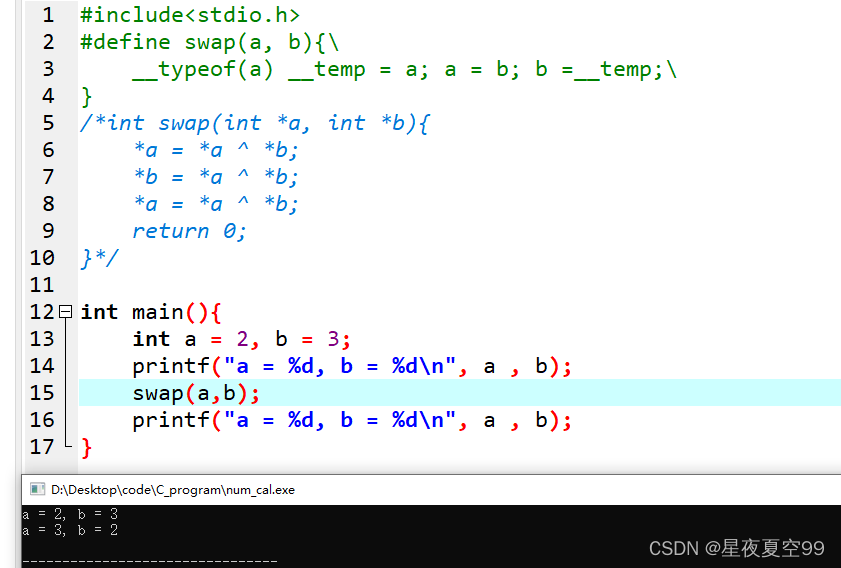
写一个函数，函数功能为交换两个变量的值。

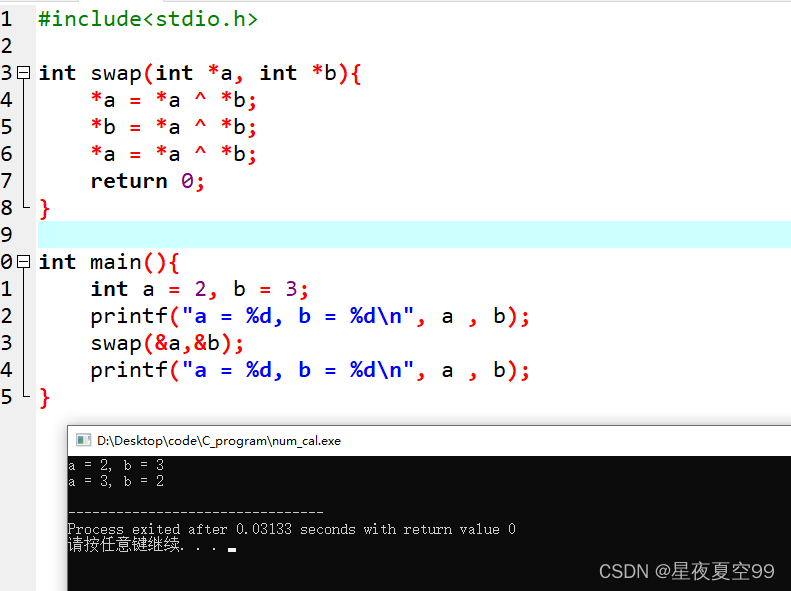
这道题的一般思路就是创建一个临时变量，存储原值，然后再相互赋值完成交换，但是当我们了解了异或之后，完全不用创建中间变量来存储。

#include<stdio.h>int swap(int *a, int *b){*a = *a ^ *b;*b = *a ^ *b;*a = *a ^ *b;return 0;
}
int main(){int a = 2, b = 3;printf("a = %d, b = %d\n", a , b);swap(&a,&b);printf("a = %d, b = %d\n", a , b);
}

在这里插入图片描述
左移“<<”和右移“>>”
顾名思义左移就是把整个二进制数据向左移动，右移就是向右移动。左移右移是二进制环境下进行的，我们假设在十进制环境中163，左移一位就是1630，右移就是16.3下取整就是16。十进制中左移就是乘以10，右移就是除以10。二级制与十进制的区别就是位权发生了变化，那么在计算机中的二进制环境下左移就是乘以2，右移就是除以2(同样也是下取整)。
在这里插入图片描述

数学函数库

头文件: math.h

常用函数	常用函数
pow(a,b)	fabs
sqrt(n)	log(n)
ceil(n)	log10(n)
floor(n)	acos(n)
abs(n)(stdlib.h)	…

pow()函数

pow()函数：指数函数头文件：math.h原型： double pow(double a, double b)a:底数b:指数返回值：a的b次幂例子：pow(2,3) = 8

sqrt()函数

sqrt()函数：平方根函数头文件：math.h原型： double pow(double x)x:被开方数返回值：x的平方根例子：sqrt(16) = 4

ceil()函数

ceil()函数：上取整函数头文件：math.h原型： double ceil(double x)x: 某个实数返回值：|x|例子：ceil(4.1) = 5

floor ()函数

floor()函数：下取整函数头文件：math.h原型： double floor(double x)x:某个实数返回值：|x|例子：floor(5.9) = 5

abs()函数

abs()函数：绝对值函数头文件：stdlib.h原型： int abs(int x)x:某个实数返回值：|x|例子：abs(-5) =5

fabs()函数

fabs()函数：实数数绝对值函数头文件：math.h原型： double fabs(double x)x: 某个实数返回值：|x|例子：fabs(-4.9) = 4.9

log()函数

log()函数：对数函数头文件：math.h原型： double log(double x)x:某个实数返回值：以e为底的x的对数例子：log(9) = 2.197225...

log10()函数

log10()函数：对数函数头文件：math.h原型： double log10(double x)x:某个实数返回值：以10为底的x的对数例子：log10(1000) = 3

可以通过换底公式求得不同的对数 $log_26 = \frac{log_{10}6}{log_{10}2}$

acos()函数

acos()函数：对数函数头文件：math.h原型： double acos(double x)x:某个实数返回值：返回arccos(x)例子：acos(-1) = 3.1415926...

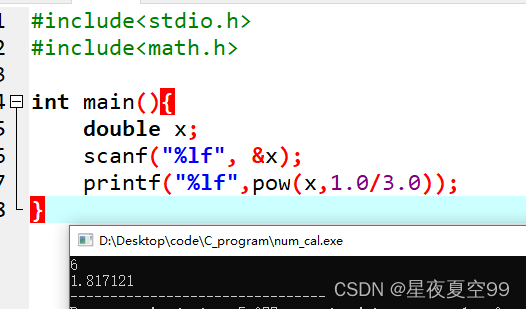
写一个程序，输入一个数字，输出一个数字的立方根。
这道题需要注意的是，函数的数据类型是double。

拓展

在上面交换两个变量的值的问题中还可以采用宏的方式。这个采用的思路就是使用中间变量的方式，宏的好处就是运算速度更快，当然也可以在宏当中采用异或的方法。在这里主要是想多展示一下__typeof()，它实际上是内置的一个宏，就是参数的数据类型。
另外就是我们应该也更多的取了解宏的用法。
在这里插入图片描述