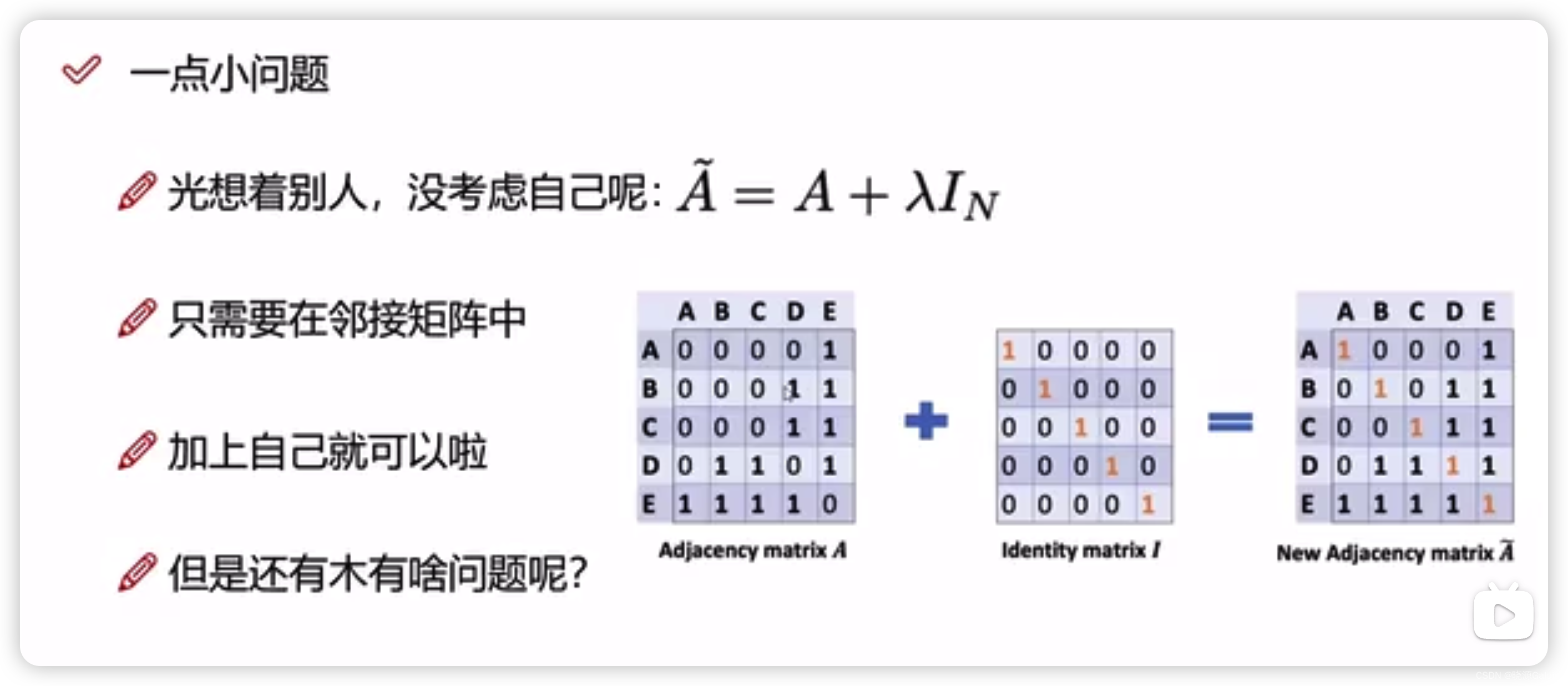
由于邻接矩阵中一般不会（i,i）等于1，除非第i个点上有自环。
而如果用邻接矩阵去乘上特征矩阵，那么将丢失自身向自身的贡献。
此时可以再邻接矩阵的基础上，再加上一个单位阵，从而使得最终的结果包含自身对整体的贡献。
但这样仍会存在问题。
就是忽略了各个点对系统的贡献比例。
也就是说需要再做一个加权平均的过程。
这个时候就可以借助度矩阵来解决这个问题

将新矩阵的每个点的度来组成对角矩阵。
并求出对角矩阵的逆矩阵。
从而得到用于求取平均值的矩阵。

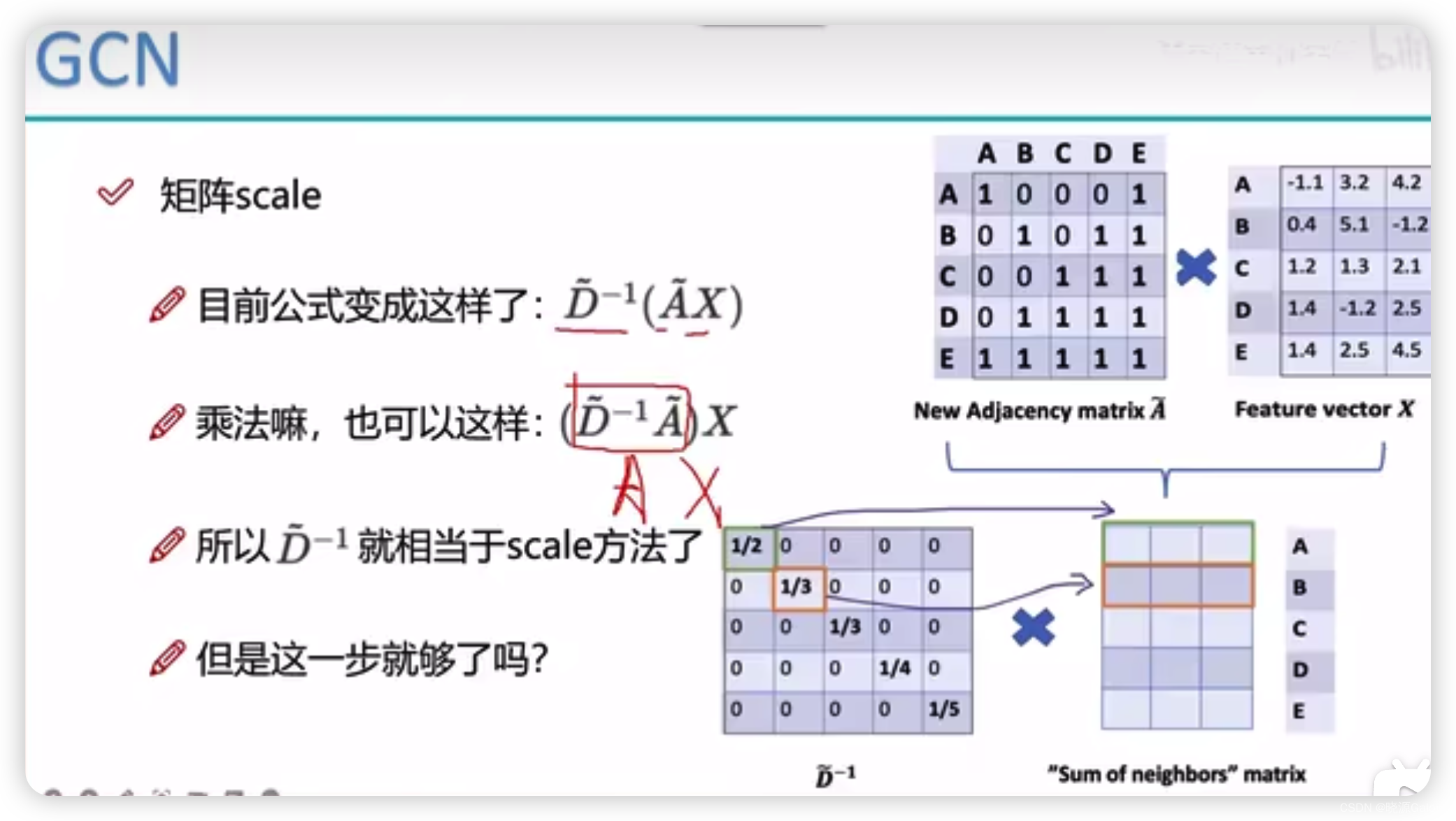
左乘度矩阵的逆只是对行向量做归一化。于是需要右乘上一个矩阵对列向量做归一化。

而这就相当于矩阵内同一个元素做了两次归一化，于是可以将度矩阵开个方（将对角矩阵开方是可以做到的）