行内公式 f ( x ) = a + b f(x)=a+b f(x)=a+b
左右各加一个$,即为行内公式
$ f(x) = a+b $
行间公式
$$ f(x) = a+b $$
f ( x ) = a + b f(x)=a+b f(x)=a+b
手动编号
$$ f(x) = a - b \tag{1.1} $$
f ( x ) = a − b (1.1) f(x)=a-b \tag{1.1} f(x)=a−b(1.1)
简单运算
+-*/以及阿拉伯字母都可以直接输入获得
使用命令\cdot表示乘法的原点,\neq表示不等号,\equiv表示恒等于,\bmod表示取模,\times表示×,\quad表示四个空格$$ x+2-3*4/6=4/y + x\cdot y $$x + 2 − 3 × 4 / 6 = 4 / y + x ⋅ y x+2-3\times4/6=4/y + x\cdot y x+2−3×4/6=4/y+x⋅y
$$ 0 \neq 1 \quad x \equiv x \quad 1 = 9 \bmod 2 $$
0 ≠ 1 x ≡ x 1 = 9 m o d 2 0 \neq 1 \quad x \equiv x \quad 1=9 \bmod 2 0=1x≡x1=9mod2
上下标
_表示下标,^表示上标
当上下标内容不止一个字符时,需要使用大括号括起来
单引号'表示求导
~可以进行分割
$$ a_{ij}^{2} + b^3_{2}=x^{t} + y' + x''_{12} $$
a i j 2 + b 2 3 = x t + y ′ + x 12 ′ ′ a_{ij}^{2} + b^3_{2}=x^{t}+y'+x''_{12} aij2+b23=xt+y′+x12′′
根号、分式
\sqrt表示平方根,\sqrt[n]表示n次方根,\frac表示分式
$$\sqrt{x} + \sqrt{x^{2}+\sqrt{y}} = \sqrt[3]{k_{i}} - \frac{x}{m}$$
x + x 2 + y = k i 3 − x m \sqrt{x} + \sqrt{x^{2}+\sqrt{y}} = \sqrt[3]{k_{i}}-\frac{x}{m} x+x2+y=3ki−mx
上下标记
\overline,\underline表示上下方画水平线
只能覆盖一个字母,是bug
$$\overline{x} \qquad \underline{a}$$
x ‾ a ‾ \overline{x} \qquad \underline{a} xa
向量
\vec表示向量,\overrightarrow表示箭头向右的向量,\overleftarrow表示箭头向左的向量
$$\vec{a} + \overrightarrow{AB} + \overleftarrow{DE}$$
a ⃗ + A B → + D E ← \vec{a} + \overrightarrow{AB} + \overleftarrow{DE} a+AB+DE
积分、极限、求和、乘积
\int表示积分,\lim表示极限, \sum表示求和,\prod表示乘积,在这些操作中,^、_表示上、下限
\to 右指箭头,\mathrm,d微分
$$ \lim_{x \to \infty} x^2_{22} - \int_{1}^{5}x\mathrm{d}x + \sum_{n=1}^{20} n^{2} = \prod_{j=1}^{3} y_{j} + \lim_{x \to -2} \frac{x-2}{x} $$
lim x → ∞ x 22 2 − ∫ 1 5 x d x + ∑ n = 1 20 n 2 = ∏ j = 1 3 y j + lim x → − 2 x − 2 x \lim_{x \to \infty} x^2_{22}-\int_{1}^{5}x\mathrm{d}x+\sum_{n=1}^{20}n^{2}=\prod_{j=1}^{3}y_{j}+\lim_{x \to -2}\frac{x-2}{x} x→∞limx222−∫15xdx+n=1∑20n2=j=1∏3yj+x→−2limxx−2
三个原点
\ldots点位于基线上,\cdots点设置为居中,\vdots使其垂直,\ddots对角线排列
$$ x_{1},x_{2},\ldots,x_{5} \quad x_{1} + x_{2} + \cdots + x_{n} $$
x 1 , x 2 , … , x 5 x 1 + x 2 + ⋯ + x n x_{1},x_{2},\ldots,x_{5} \quad x_{1}+x_{2}+ \cdots +x_{n} x1,x2,…,x5x1+x2+⋯+xn
重音字符
$ \hat{x} $$ \hat{x} $$ \tilde{x} $
x ^ x ˉ x ~ \hat{x} \quad \bar{x} \quad \tilde{x} x^xˉx~
矩阵
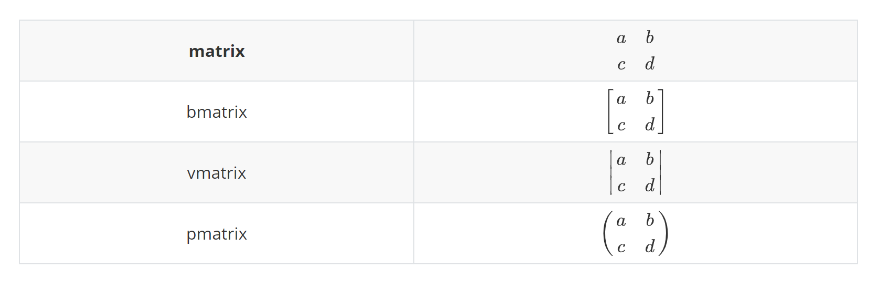
[ 1 2 ⋯ 67 95 ⋯ ⋮ ⋮ ⋱ ] \begin{bmatrix} 1 & 2 & \cdots\\ 67 & 95 & \cdots\\ \vdots & \vdots & \ddots \\ \end{bmatrix} 167⋮295⋮⋯⋯⋱
希腊字母
在LaTeX中通过反斜杠 \加上其字母读音实现,将读音首字母大写即可输入其大写形式,详见下表

$$ \alpha^{2} + \beta = \Theta $$
α 2 + β = Θ \alpha^{2} + \beta = \Theta α2+β=Θ
公式组合
通过cases环境实现公式的组合,&分隔公式和条件,还可以通过\limits来让x→0位于lim的正下方而非默认在lim符号的右下方显示
$$D(x) = \begin{cases}
\lim\limits_{x \to 0} \frac{a^x}{b+c}, & x<3 \\
\pi, & x=3 \\
\int_a^{3b}x_{ij}+e^2 \mathrm{d}x,& x>3 \\
\end{cases}$$
D ( x ) = { lim x → 0 a x b + c , x < 3 π , x = 3 ∫ a 3 b x i j + e 2 d x , x > 3 D(x)=\begin{cases} \lim\limits_{x \to 0} \frac{a^x}{b+c},& x<3 \\ \pi,&x=3\\ \int_a^{3b}x_{ij}+e^2\mathrm{d}x,& x>3 \\ \end{cases} D(x)=⎩ ⎨ ⎧x→0limb+cax,π,∫a3bxij+e2dx,x<3x=3x>3
拆分单个公式
$$\begin{split}
\cos 2x &= \cos^2x - \sin^2x \\
&=2\cos^2x-1
\end{split}$$
cos 2 x = cos 2 x − sin 2 x = 2 cos 2 x − 1 \begin{split} \cos 2x&=\cos^2x -\sin^2x\\ &=2\cos^2x-1 \end{split} cos2x=cos2x−sin2x=2cos2x−1
粗体——可以表示向量
$$ \boldsymbol{a} $$
存在、任意、空集
$\forall$ 任意
$\varnothing$ 空集
并集、交集
$\cup$
属于、不属于
$\in$
$\notin$
大于等于、小于等于
大于等于:`\geq`
小于等于:`\leq`