本篇博客将详细介绍什么是数学建模。
文章目录
- 个人简介
- 什么是数学建模
- (一)引例:高中数学里的简单线性规划问题
- 数学建模的定义及用途
- 数学建模的定义
- 数学建模的用途
- 正确认识数学建模
个人简介
本人在本科阶段获得过国赛省一、mathorcup数学建模一等奖、五一杯数学建模一等奖、华数杯数学建模一等奖、亚太杯数学建模一等奖和两次美赛一等奖。自己在数学建模这条路上摸爬滚打了几年,现在想借助博客分享自己在数学建模上的一些经验,帮助小白更快地学习数学建模。
什么是数学建模
(一)引例:高中数学里的简单线性规划问题
在了解什么是数学建模之前,我们先来复习一下高中数学里的简单线下规划问题。
线性规划问题:求线性目标函数在线性约束条件下的最大值或最小值的问题,通常称为线性规划问题。
我们来看2018年理科数学全国I卷的一道题目:

一般而言,求解线性规划问题一共有四步:
1、列出线性约束条件,确定目标函数
2、画出可行域
3、在可行域中移动目标函数,找出最优解
4、求出最值
针对这个题,约束条件和目标函数如下:

根据约束条件画出可行域,具体如下图:
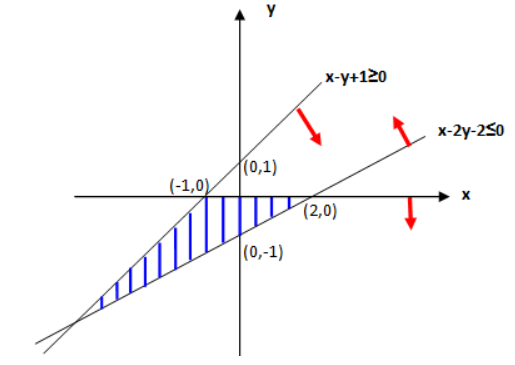
蓝色部分即为可行域。
在移动目标函数之前,现将目标函数化简成 y = k x + m z y=kx+mz y=kx+mz的形式,即 z = 3 x + 2 y z=3x+2y z=3x+2y换成 y = − 3 2 x + 1 2 z y=-\frac{3}{2}x+\frac{1}{2}z y=−23x+21z。已知题目中求 z z z的最大值,其实也就是求 y = − 3 2 x + 1 2 z y=-\frac{3}{2}x+\frac{1}{2}z y=−23x+21z这条直线在 y y y轴截距的最大值。
接下来令 z = 0 z=0 z=0,画出 y = − 3 2 x y=-\frac{3}{2}x y=−23x的图像,如下图绿色系所示,可知当直线 y = − 3 2 x y=-\frac{3}{2}x y=−23x向右移动到(2,0)点时与y轴截距最大,如下图粉色直线的位置,此时(2,0)即为最优解。
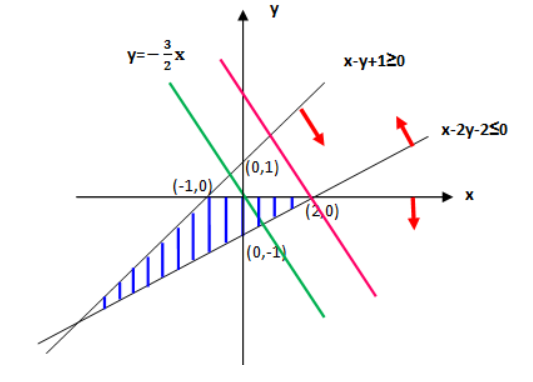
因此, z m a x = 3 ∗ 2 + 2 ∗ 0 = 6 z_{max}=3*2+2*0=6 zmax=3∗2+2∗0=6。
这道题到这里就做完了。介绍这道题的目的是让大家了解高中数学里的简单线性规划。下面再看一道高中数学里的简单线性规划的大题。
某工厂生产甲、乙两种产品,每生产1吨产品需要的电力、煤、劳动力及产值,如下表所示:
品种 电力(千度) 煤(吨) 劳动力(人) 产值(千元) 甲 4 3 5 7 乙 6 6 3 9 该厂的劳动力满员150人,根据限额每年用电不超过180千度,用煤每天不得超过150吨,问每天生成这两种产品各多少时,才能创造最大的经济效益。
按照前面的讲解,首先设每天生产甲产品 x x x吨,乙产品 y y y吨,可得产值 z z z千元。因此,目标函数为: z = 7 x + 9 y z=7x+9y z=7x+9y。按照题目要求,设置约束条件如下:
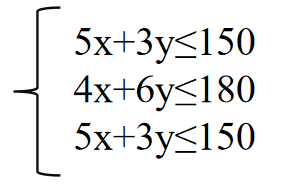
紧接着画出可行域,如下图所示:
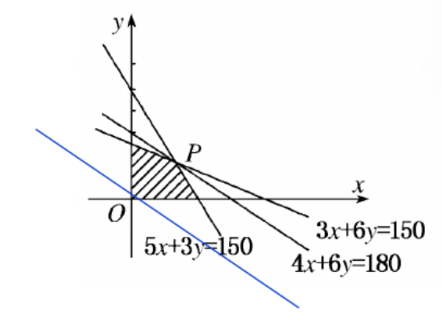
因为 y = − 7 9 x + 1 9 z y=-\frac{7}{9}x+\frac{1}{9}z y=−97x+91z,所以画出直线 y = − 7 9 x y=-\frac{7}{9}x y=−97x,并平移得到P点,此时 z z z最大。求出P点为( 150 7 \frac{150}{7} 7150, 100 7 \frac{100}{7} 7100),因此每天生产甲产品 150 7 \frac{150}{7} 7150吨,乙产品 100 7 \frac{100}{7} 7100吨。
如果能看懂这个例子,那么就可以称自己数学建模入门了。
数学建模的定义及用途
数学建模的定义
为什么学到这就可以称自己数学建模入门了呢?我们先来看看数学建模的定义:
数学建模是指根据实际问题来建立数学模型,对数学模型进行求解,然后再根据结果解决实际问题。
我们再回到上面那个应用题,题目本身就是实际问题,而我们建立的模型就是数学模型,根据这个模型我们得到了最终的结果,这难道不是数学建模吗?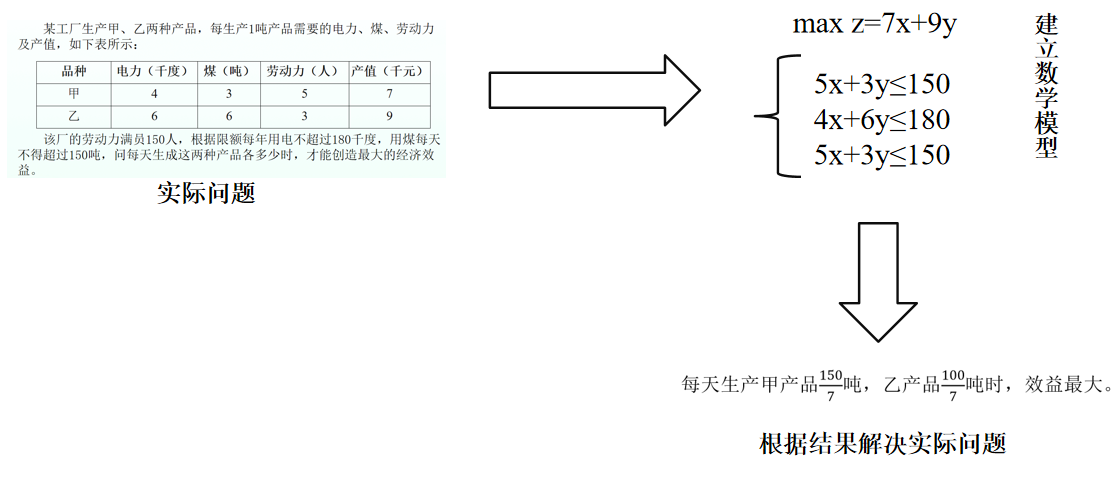
有数学建模基础的同学可能知道,上面这种题目就是数学建模里的优化问题,这部分将在后面的博客中详细讲解。
数学建模的用途
在各个学科和行业中,数学建模都扮演着重要的角色,帮助解决复杂的实际问题。例如:
1、环境科学:如预测天气、模拟气候变化、水资源管理等。
2、计算机科学:如优化算法、图像识别等。
3、交通运输:如交通流量预测、交通信号优化等。
4、金融领域:如股票价格预测、风险管理等。
5、医学:如疾病传播模型、药物效果评估等。
6、社会科学:如研究人类行为、社会网络分析等。
7、教育:如教学效果评估、排课问题等。
8、市场营销:如广告效果评估、市场份额预测等。
正确认识数学建模
数学模型一般是实际事物的一种数学简化。它常常是以某种意义上接近实际事物的抽象形式存在的,但它和真实的事物有着本质的区别,例如:
1、为了进行数学分析,问题通常需要被简化,舍弃一些次要的、难以处理的细节,以便应用数学方法求解。 现实世界的问题通常更为复杂,包含许多不确定性、非线性关系和随机因素,这些在数学建模中可能被简化或省略。
2、在数学建模中常常需要引入一些假设,以使问题变得更容易处理,同时也要考虑到数学模型的适用性。而实际问题通常受到各种现实约束,如资源限制、时间限制、技术可行性等,需要考虑多种因素。
3、模型的准确性受到模型假设和简化的影响,有时候可能只是对实际问题的近似。
本篇博客到此结束!