1. 流形学习
作为机器学习研究的热点问题之一,流形学习是要从高维数据集中发现内在的低维流形,并基于低
维流形来实现随后的各种机器学习任务,如模式识别,聚类分析。与欧氏空间不同,流形学习主要
处理的是非欧空间里的模式识别和维数约简等问题。从宇宙空间看地球,如果不借助外界力量的
话,我们只能局限于地球的表面活动,而且地球上两点的距离并不单纯是它们对应的直线的跟离,
而是测地线距离。可以证明,我们生活的地球是一个嵌入在3维欧式空间中的维流形,也就是说,
地球表面点的位置可由两个变量来控制。
从定义我们可以看出,流形就是局部欧式的拓扑空间,欧式空间的性质只在邻域内有效。值得指出
的是,当邻域定义为整个欧氏空间时,欧氏空间本身也可以视为流形。所以,流形学习并非是一种
特殊学习方法,而是基于欧氏度量学习的一种推广,具有更强的一般性。
定义:设M是一个Hausdorff拓扑空间,若对∀p∈M,都有p的邻域U和Rm的一个开集同胚,则称M
为m维拓扑流形。
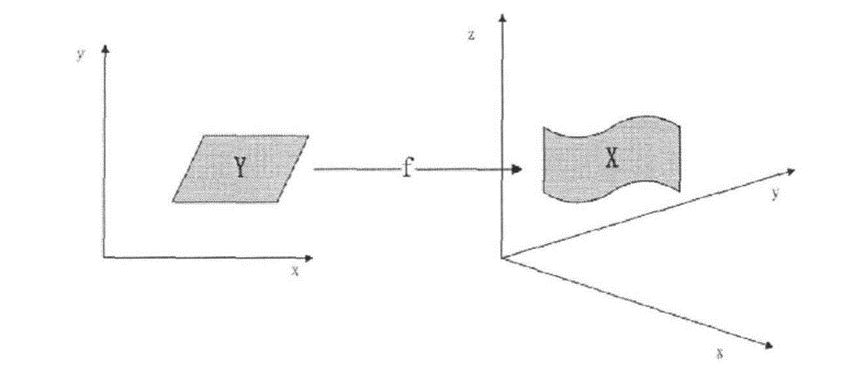
我们假设这些观测数据是由一些隐变量Y通过一个映射f:Y->X生成的,其中![]() ,
,
于是流形学习的任务就是通过观测数据把未知映射f和隐变量Y重建出来。由于m<n,故该问题是一
个病态问题,不存在唯一解,因此研究人员提出了各种各样的流形学习算法,它们试图通过添加某
些特定约束用以恢复流形的内在结构。
总体来说,流形学习兴起来源于2000年在《科学》杂志上的两篇关于流形学习的文章,其中一篇
提出了一个叫ISOMAP的方法,该方法把传统的MDS算法扩展到非线性流形上,通过对中心化的测
地线距离矩阵进行特征值分解来保持流形上的整体拓扑结构。而另一篇文章提出厂局部线性嵌入
(Local Linear Embedding (LLE))算法,该算法假设高维数据和低维数据的局部拓扑结构关系保持
不变,即邻域关系不变,然后刊用这种关系从高维数据重构出低维的流形嵌入。
1.1 PCA

该方法认为特征的方差越大提供的信息量越多,特征的方差越小提供的信息量越少。PCA 通过原
分量的线性组合构造方差大、含信息量多的若干主分量,从而降低数据的维数。
1.2 MDS

其中(a)为真实数据集的流形结构图,(b)为从(a)随机采样 2000 个点后的数据分布图,
(c)、(d)和(e)为经三次不同采样后,采样点经 MDS 算法降到二维空间后分布图。可以看
出,(c)图在一定程度上保持了数据的连续性,但并没有发现嵌入在数据的本质,改变了采样点
的拓扑结构;(d)和(e)图的效果更差,不同样本点均发生了不同程度的重叠,严重改变了采样
点的结构。
1.3 ISOMAP

Laplacian Eigenmap(LE)就是其中的一种,该算法首先构造一个邻域关系图,然后对该图的拉普拉
斯矩阵进行特征值分解来得到流形的低维表示,这样的分解保持了数据的局部关系,注意到在LE
中,我们要估计流形上的Laplacian算子。Hessian Eigenmap(HLLE) 该算法通过估计流形上的
Heosian算子,然后对该算子进行特征值分解来保持流形的局部拓扑性。SDE算法:为了得到一个
等距嵌入,用半正定规划的方法估计流形上的点对间的角度和距离,从而学习图像数据中的流形。
2. 流行学习框架
2.1 线性降维的不足
原始数据无法表示为特征的简单线性组合,比如:PCA无法表达Helix曲线流形。

真实数据中的有用信息不能由线性特征表示,比如:如何获取并表示多姿态人脸的姿态信息

比如:如何获取运动视频序列中某个动作的对应帧

2.2 流形学习框架
流形是线性子空间的一种非线性推广,拓扑学角度:局部区域线性,与低维欧式空间拓扑同胚,微
分几何角度:有重叠chart的光滑过渡,黎曼流形就是以光滑的方式在每一点的切空间上指定了欧
氏内积的微分流形。
流形学习是一种非线性的维数约简方法,高维观察数据的变化模式本质是由少数几个隐含变量所决
定的,如:人脸采样由光线亮度、人与相机的距离、人的头部姿势、人的面部表情等因素决定。从
认知心理学的角度,心理学家认为人的认知过程是基于认知流形和拓扑连续性的。
设![]() 是一个低维流形,
是一个低维流形,![]() 是一个光滑嵌入,其中 D>d 。数据集
是一个光滑嵌入,其中 D>d 。数据集![]() 是随机生成的,
是随机生成的,
且经过 f 映射为观察空间的数据![]() 。流形学习就是在给定观察样本集
。流形学习就是在给定观察样本集![]() 的条件下重
的条件下重
构 f 和![]() 。
。
经典流形学习方法一览:

3. 方法
3.1 等距映射(ISOMAP)
保持全局测地距离,测地距离反映数据在流形上的真实距离差异。
等距映射,基于线性算法MDS,采用“测地距离”作为数据差异度量。

MDS的示意图: MDS失效:

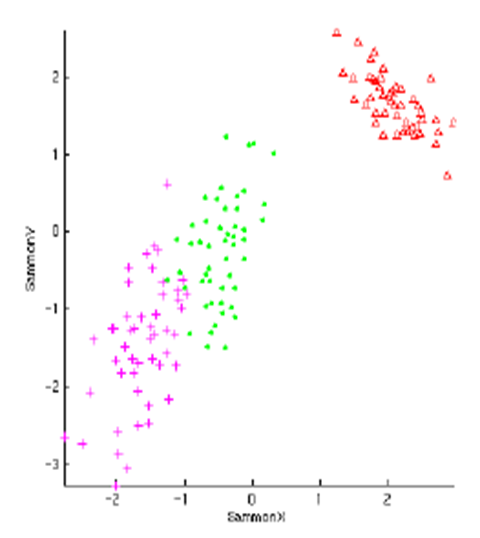
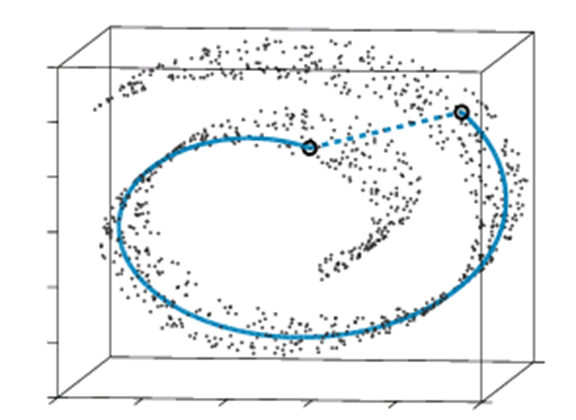
ISOMAP算法流程:
①计算每个点的近邻点 (用K近邻或ξ邻域)
②在样本集上定义一个赋权无向图,如果![]() 和
和![]() 互为近邻点,则边的权值为
互为近邻点,则边的权值为![]()
③计算图中两点间的最短距离,记所得的距离矩阵为![]()
④用MDS求低维嵌入坐标,令![]() ,低维嵌入是
,低维嵌入是
![]() 的第1大到第 d大的特征值所对应的特征向量。
的第1大到第 d大的特征值所对应的特征向量。
图距离逼近测地距离:
假设采样点是随机均匀抽取的,则渐进收敛定理 给定![]() ,则只要样本集充分大且适当选
,则只要样本集充分大且适当选
择K , 不等式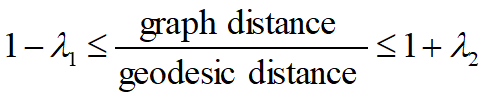 ,至少以概率
,至少以概率![]() 成立。
成立。
前提假设:数据所在的低维流形与欧式空间的一个子集整体等距,该欧式空间的子集是一个凸集。
思想核心:较近点对之间的测地距离用欧式距离代替,较远点对之间的测地距离用最短路径来逼近
算法特点:适用于学习内部平坦的低维流形,不适于学习有较大内在曲率的流形,计算点对间的最
短路径比较耗时。
继承了MDS和PCA的特点:保证渐近收敛于真结构,多项式运行时,发现任意维度流形的能力,
当数据来自单个采样良好的集群时,性能会很好。少数自由参数:为其度量保持特性提供了良好的
理论基础。
嵌入是有偏差的,以保持远点的分离,这可能导致局部几何的扭曲,不能很好地投影分布在多个集
群中的数据,条件良好的算法,但对于大数据集计算成本高,保角等高图——能够学习某些弯曲流
形的结构,Landmark Isomap——通过一个小得多的计算集来近似大的全局计算,使用k/2个最近
的物体和k/2个最远的物体重建距离。
3.2 局部线性嵌入(LLE)
前提假设:采样数据所在的低维流形在局部是线性的,每个采样点均可以利用其近邻样本进行线性
重构表示。学习目标:低维空间中保持每个邻域中的重构权值不变,在嵌入映射为局部线性的条件
下,最小化重构误差,最终形式化为特征值分解问题。
LLE算法流程:
①计算每一个点![]() 的近邻点, 一般采用K 近邻或者ξ邻域
的近邻点, 一般采用K 近邻或者ξ邻域
②计算权值![]() ,使得把
,使得把![]() 用它的K个近邻点线性表示的误差最小,即通过最小化
用它的K个近邻点线性表示的误差最小,即通过最小化![]() 来求
来求
出![]() 。
。 ![]()
③保持权值![]() 不变, 求
不变, 求![]() 在低维空间的象
在低维空间的象![]() ,使得低维重构误差最小。
,使得低维重构误差最小。
![]()
LLE算法的求解:
①计算每一个点![]() 的近邻点
的近邻点
②对于点![]() 和它的近邻点的权值
和它的近邻点的权值![]() ,
,
③令![]()
![]() ,低维嵌入是 M 的最小的第 2到第 d+1 个特征向量。
,低维嵌入是 M 的最小的第 2到第 d+1 个特征向量。
LLE (Locally linear embedding):优点:算法可以学习任意维的局部线性的低维流形,算法归结为
稀疏矩阵特征值计算,计算复杂度相对较小。
缺点:算法所学习的流形只能是不闭合的,算法要求样本在流形上是稠密采样的,算法对样本中的
噪声和邻域参数比较敏感。用于计算W的协方差矩阵可能是病态的,需要用到正则化。较小的特征
值受到数值精度误差和混合的影响,但是,该算法中使用的稀疏矩阵使其比Isomap更快。
3.3 拉普拉斯特征映射(Laplacian Eigenmap)
设 G 是一个图,v 是它的顶点,![]() 是 v 的自由度,w(u,v)是连接顶点u、v的边的权值,令
是 v 的自由度,w(u,v)是连接顶点u、v的边的权值,令
 ,
,![]() 其中 T 是对角矩阵,对角线的元素为
其中 T 是对角矩阵,对角线的元素为
 ,则称 L 为图 G 上的拉普拉斯算子。
,则称 L 为图 G 上的拉普拉斯算子。
Laplacian Eigenmap 算法流程:
①从样本点构建一个近邻图,图的顶点为样本点,离得很近两点用边相连 (K近邻或ξ邻域)
②给每条边赋予权值,如果第i个点和第j个点不相连,权值为0,否则![]()
③计算图拉普拉斯算子的广义特征向量,求得低维嵌入。令D为对角矩阵![]()
L是近邻图上的拉普拉斯算子,求解广义特征值问题![]()
LE (Laplacian Eigenmap)优点:算法是局部非线性方法,与图理论有很紧密的联系。算法通过
求解稀疏矩阵的特征值问题解析地求出整体最优解,效率非常高。算法使原空间中离得很近的点在
低维空间也离得很近,可以用于聚类。
缺点:同样对算法参数和数据采样密度较敏感,不能有效保持流形的全局几何结构。