Leetcode 494 目标和-编程知识

Leetcode 494 目标和

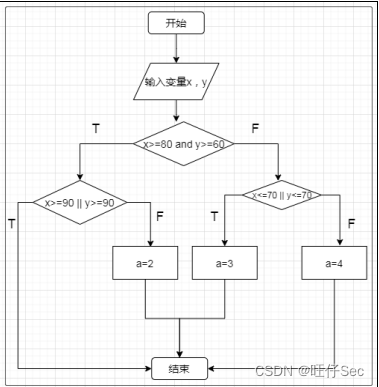
题意理解：

        给你一个非负整数数组 nums 和一个整数 target 。

        向数组中的每个整数前添加 '+' 或 '-' ，然后串联起所有整数，可以构造一个 表达式 ：

例如，nums = [2, 1] ，可以在 2 之前添加 '+' ，在 1 之前添加 '-' ，然后串联起来得到表达式 "+2-1" 。

        返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。



简单来说：就是在元素前面加‘+’或‘-’使其结果值为target。

可以将其思路转换为：将数组元素分为两部分，其差为target。

则有part1-part2=target，part1+part2=sum

part1=(sum+target)/2



固有我们需要将数组元素分为两部分，一部分较大的为part1=(sum+target)/2,较小的部分为part2=(sum-target)/2。

此时，我们再次转变思路：将其构造成0-1背包问题：

背包大小为m=(sum+target)/2

物品为[0,n]的元素，其价值和重量都是nums[]

接下来，使用动态规划中的0-1背包思路解决问题。

解题思路：

  首先理解题意，将其转换为一个背包问题，使用动态规划的思路来求解。

动态规划五部曲：

（1）dp[i][j]或dp[i]的含义

（2）递推公式

（3）根据题意初始化

（4）遍历求解:先遍历包还是先遍历物品

（5）打印——debug

1.动态规划二维dp数组

dp[i][j]表示[0,i]的元素装满大小为j的背包有多少种方法。
递推公式：dp[i][j]=dp[i-1][j]+dp[i-1][j-nums[i]]，
1. 当当前物品大于当前背包的大小时，放满大小为j的背包的方法数仍就为dp[i-1][j].
2. 当当前物品小于等于当前背包的大小时，放满大小为j的背包的方法数=dp[i-1][j]+dp[i-1][j-nums[i]]，其中dp[i-1][j-nums[i]]是增加了物品nums[i]后增加的方法数。
初始化：初始化第一列，其中特别的：放满背包大小0 有多少种方法——要么什么也不放，要么放入大小为0的物品。初始化时要根据问题，具体分析。
遍历：由于二维数组保留了两个维度所有值，所以先便利包还是先遍历物品都可以

public int findTargetSumWays(int[] nums, int target) {int sum=0;for(int num:nums){sum+=num;}//是否能按照需求分成两部分if((sum+target)%2!=0) return 0;if((sum-target)%2!=0) return 0;//把所有值当作整数，分成两部分一正一负即可，所以如果target总保持为正数if(target<0) target=-target;int size= (int)Math.ceil((float)(sum+target)/2);int dp[][]=new int[nums.length][size+1];//初始化for(int[] temp:dp) Arrays.fill(temp,0);int countZero=0;for(int i=0;i<nums.length;i++){if(nums[i]==0) countZero++;dp[i][0]=countZero+1;}for(int j=1;j<=size;j++){if(nums[0]==j) dp[0][j]=1;else dp[0][j]=0;}//遍历顺序for(int i=1;i< nums.length;i++){for(int j=0;j<=size;j++){if(j<nums[i]){dp[i][j]=dp[i-1][j];}else{dp[i][j]=dp[i-1][j]+dp[i-1][j - nums[i]];}}}return dp[nums.length-1][size];}

2.一维滚动数组——存储压缩

dp[j]表示装满大小为j的背包有多少种方式。
递推公式：dp[j]=max(dp[j],dp[j-weight[i]]+values[i])
初始化：右边的值总是由最左边的值推导而来,dp[0]表示使背包价值为0有多少种放置方法——要么什么也不放，要么放大小为0的物品。
遍历：由于以为滚动数组是二维dp数组的动态行滚动更新，所以遍历顺序总是先物品后背包。
注意：为了防止用同层修改过的值修改本行其他值，导致物体重复放置，故采用倒序遍历背包。

 public int findTargetSumWays(int[] nums, int target) {int sum=0;for(int num:nums) sum+=num;if((sum+target)%2!=0) return 0;if((sum-target)%2!=0) return 0;if(target<0) target=-target;int size= (int)Math.ceil((float)(sum+target)/2);int dp[]=new int[size+1];//初始化Arrays.fill(dp,0);dp[0]=1;//遍历顺序for(int i=0;i< nums.length;i++){for(int j=size;j>=nums[i];j--){dp[j] += dp[j - nums[i]];}}return dp[size];}