文章目录
- 一、决策树算法
- 1、基本思想
- 2、构成
- 1)节点
- 3)有向边/分支
- 3、分类步骤
- 1)第1步-决策树生成/学习、训练
- 2)第2步-分类/测试
- 4、算法关键
- 二、信息论基础
- 1、概念
- 2、信息量
- 3、信息熵:
- 二、ID3 (Iterative Dichotomiser 3)算法
- 1、基本思想:
- 2、熵引入
- 1)经验熵
- 2)条件熵
- 3)经验条件熵
- 4)信息增益(information gain)
- 3、算法
- 4、算法案例
- 5、算法特点
- 三、ID3算法问题
- 1、 属性筛选度量标准
- 2、 剪枝处理
- 1)问题
- 2)解决
- 3)案例
- 3、 连续值处理
- 4、 缺失值处理
- 5、不同代价属性的处理
一、决策树算法
1、基本思想
基本思想:采用自顶向下的递归方法,(以信息熵为度量)构造一棵(熵值下降最快的)树,(到叶子节点处的熵值为零)此时每个叶节点中的实例都属于同一类
2、构成
决策树是一种树型结构,由结点和有向边组成
1)节点
- 内部结点表示一个属性或特征
- 叶结点代表一种类别
3)有向边/分支
分支代表一个测试输出
3、分类步骤
1)第1步-决策树生成/学习、训练
利用训练集建立(并精化)一棵决策树,建立决策树模型。这个过程实际上是一个从数据中获取知识,进行机器学习的过程
step 1:选取一个属性作为决策树的根结点,然后就这个属性所有的取值创建树的分支。
step 2:用这棵树来对训练数据集进行分类:
- 如果一个叶结点的所有实例都属于同一类,则以该类为标记标识此叶结点。
- 如果所有的叶结点都有类标记,则算法终止
step 3:否则,选取一个从该结点到根路径中没有出现过的属性为标记标识该结点,然后就这个属性所有的取值继续创建树的分支;重复算法步骤step 2
2)第2步-分类/测试
利用生成的决策树对输入数据进行分类。对输入的记录,从根结点依次测试记录的属性值,直到到达某个叶结点,从而找到该记录所在的类。
4、算法关键
建立决策树的关键,即在当前状态下选择哪个属性作为分类依据
目标:每个分支节点的样本尽可能属于同一类别,即节点的“纯度”(purity)越来越高;最具区分性的属性!
根据不同目标函数,建立决策树主要有以下三种算法
◼ ID3: 信息增益
◼ C4.5: 信息增益率
◼ CART:基尼指数
二、信息论基础
1、概念
信息论与概率统计中,熵表示随机变量不确定性的大小,是度量样本集合纯度最常用的一种指标
2、信息量
信息量:具有确定概率事件的信息的定量度量
定义: I ( x ) = − l o g 2 p ( x ) I(x)=-log_2p(x) I(x)=−log2p(x) 其中p(x)为事件x发生的概率
3、信息熵:
事件集合的信息量的平均值。
定义: H ( x ) = ∑ i h ( x i ) = ∑ i p ( x i ) I ( x i ) = − ∑ i p ( x i ) l o g 2 p ( x i ) H(x) = \sum_{i}h(x_i)=\sum_{i} p(x_i)I(x_i)=-\sum_{i} p(x_i)log_2p(x_i) H(x)=∑ih(xi)=∑ip(xi)I(xi)=−∑ip(xi)log2p(xi)
熵定义了一个函数(概率密度函数pdf)到一个值(信息熵)的映射
p ( x ) → H p(x) → H p(x)→H (函数→数值)
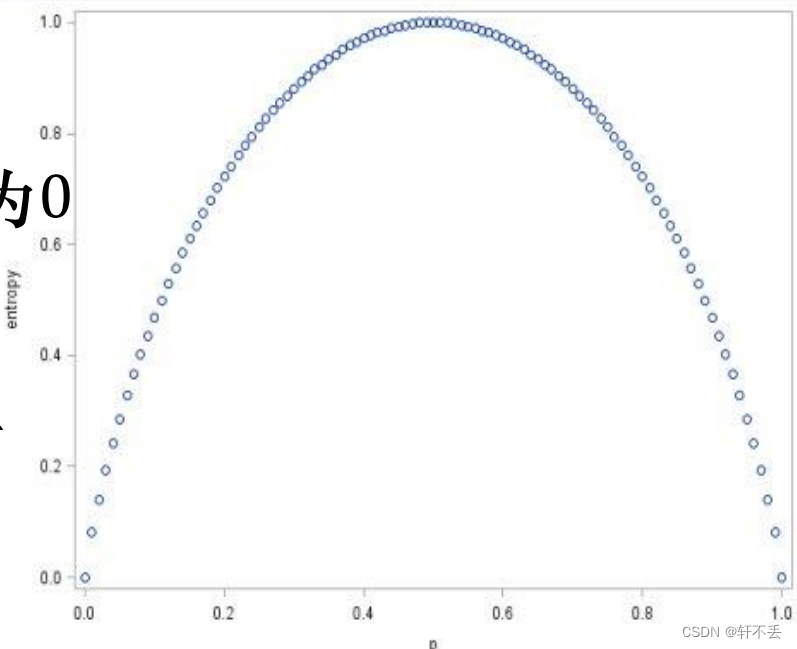
熵是随机变量不确定性的度量:
◼ 不确定性越大,熵值越大
◼ 若随机变量退化成定值,熵为0
二、ID3 (Iterative Dichotomiser 3)算法
ID3算法是一种最经典的决策树学习算法。
1、基本思想:
以信息熵为度量,用于决策树节点的属性选择,每次优先选取信息增益最大的属性,亦即能使熵值变为最小的属性,以构造一颗熵值下降最快的决策树,到叶子节点处的熵值为0。此时,每个叶子节点对应的实例集中的实例属于同一类。
熵值下降 → 无序变有序
2、熵引入
1)经验熵
假设当前样本集合D 中第c(c=1,2,…,C)类样本所占比例为 p c p_c pc(c=1,2,…,C),则D 的经验信息熵(简称经验熵)定义为:
H ( D ) = − ∑ c = 1 C p c l o g 2 p c = − ∑ c = 1 C D c D l o g 2 D c D H(D)=-\sum_{c=1}^{C}p_clog_2p_c=-\sum_{c=1}^{C}\frac{D_c}{D}log_2\frac{D_c}{D} H(D)=−∑c=1Cpclog2pc=−∑c=1CDDclog2DDc
H(D)的值越小,则D 的纯度越高
2)条件熵
对随机变量 ( X , Y ) (X, Y) (X,Y),联合分布为: p ( X = x i , Y = y i ) = p i j p(X=x_i,Y=y_i)=p_{ij} p(X=xi,Y=yi)=pij
条件熵 H ( Y ∣ X ) H(Y |X ) H(Y∣X) 表示在已知随机变量X 的条件下,随机变量Y的不确定性:
H ( Y ∣ X ) = − ∑ i = 1 n p i H ( Y ∣ X = x i ) H(Y|X)=-\sum_{i=1}^{n}p_iH(Y|X=x_i) H(Y∣X)=−∑i=1npiH(Y∣X=xi)
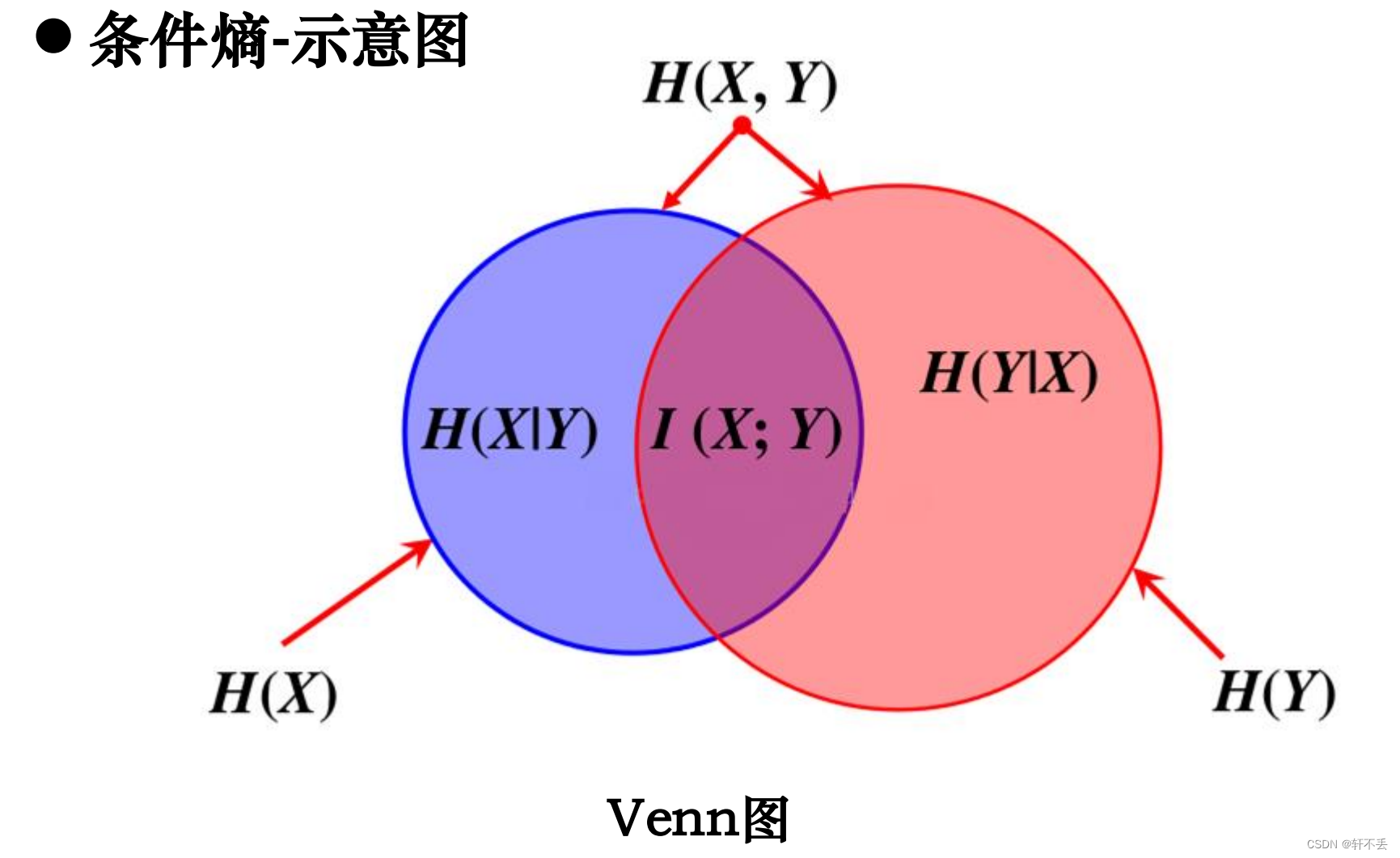
可证明:条件熵𝐻(Y|X)相当于联合熵𝐻(𝑋,𝑌)减去单独的熵𝐻(X),即
H ( Y ∣ X ) = H ( X , Y ) − H ( X ) H(Y|X)=H(X,Y)-H(X) H(Y∣X)=H(X,Y)−H(X)

3)经验条件熵

即特征a的信息对样本D 的信息的不确定性减少的程度
4)信息增益(information gain)
特征 a 对训练数据集 D 的信息增益 G ( D , a ) G(D, a) G(D,a) ,定义为集合D 的经验熵 H(D) 与特征 a 给定条件下 D 的经验条件熵 H ( D ∣ a ) H(D | a) H(D∣a) 之差,即
G ( D , a ) = H ( D ) − H ( D ∣ a ) = H ( D ) − ∑ n = 1 N D n D H ( D n ) G(D,a)=H(D)-H(D|a)=H(D)-\sum_{n=1}^{N}\frac{D^n}{D}H(D^n) G(D,a)=H(D)−H(D∣a)=H(D)−∑n=1NDDnH(Dn)
ID3算法即是以此信息增益为准则,对每次递归的节点属性进行选择的
3、算法

4、算法案例
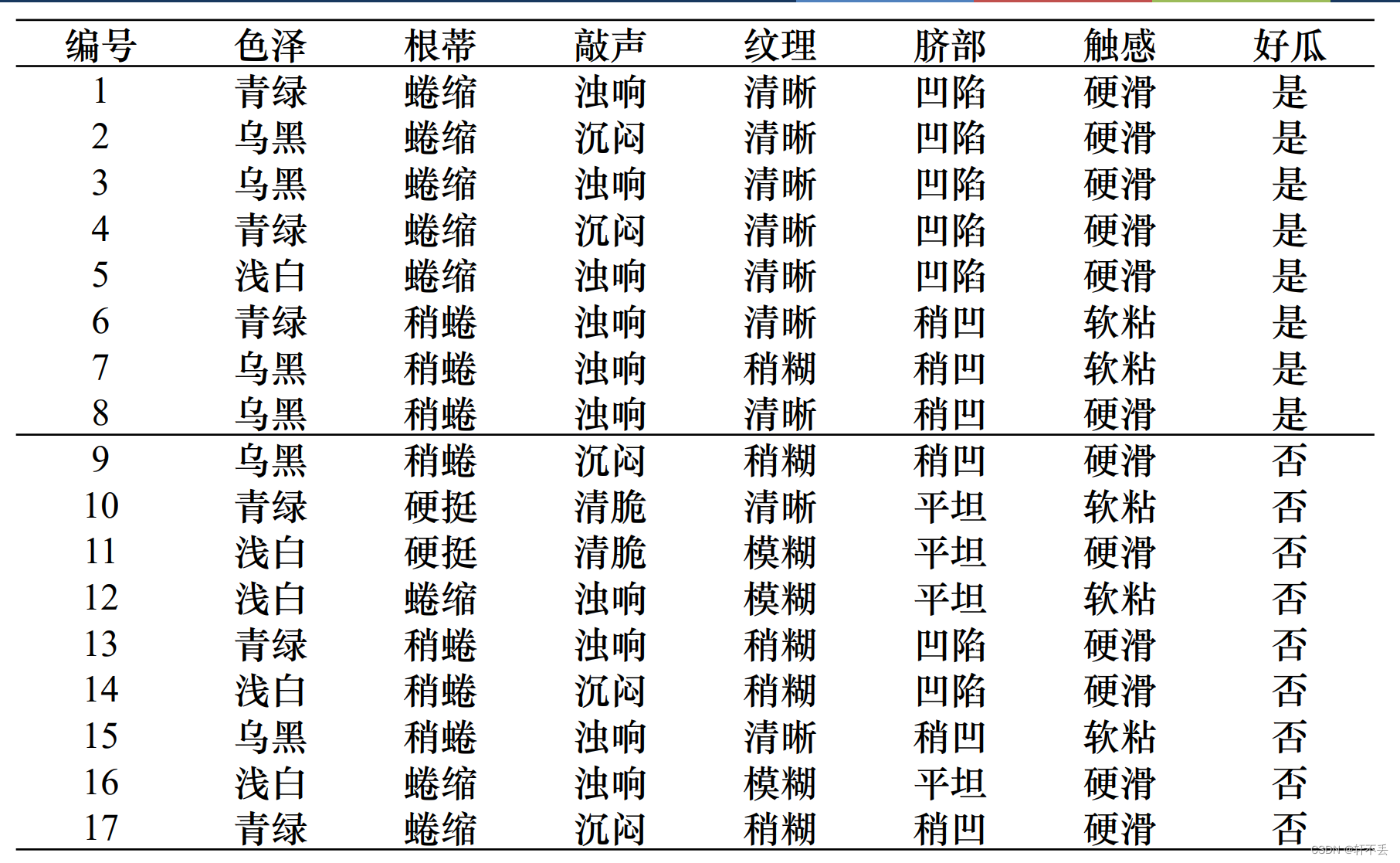


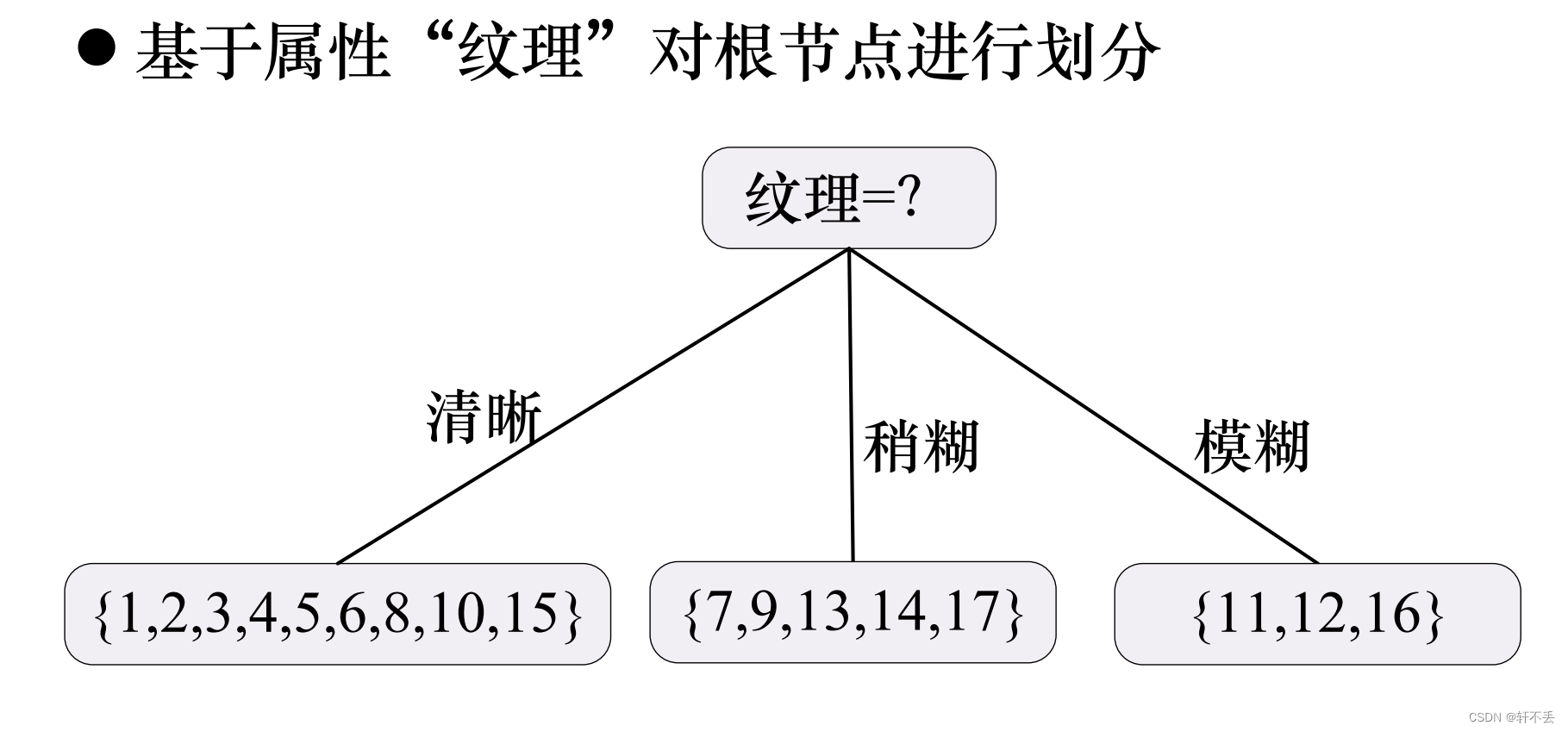

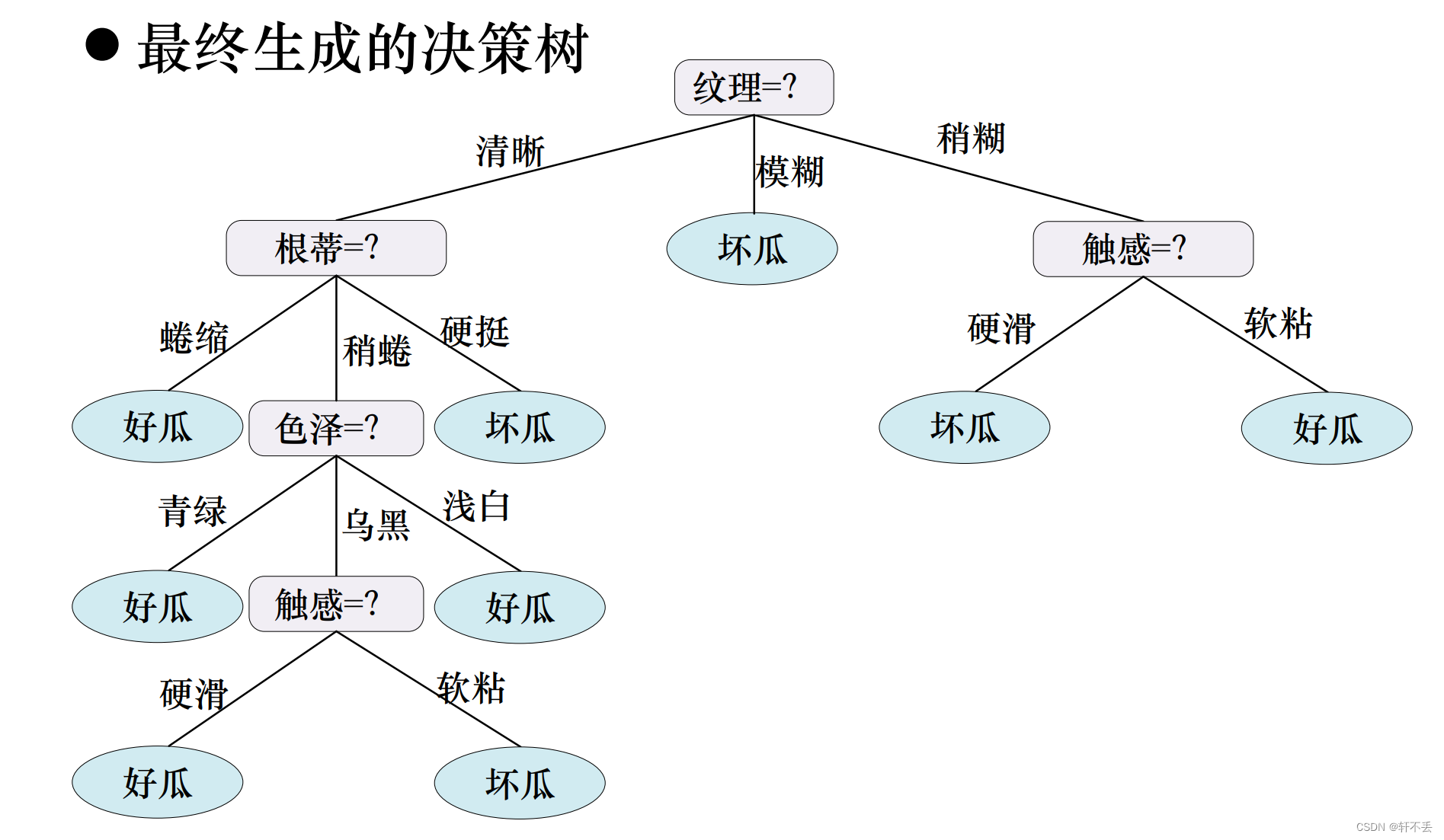
5、算法特点
最大优点是,它可以自学习:在学习的过程中,不需要使用者了解过多背景知识,只需要对训练实例进行较好的标注,就能够进行学习。
决策树的分类模型是树状结构,简单直观,比较符合人类的理解方式。
可将决策树中到达每个叶节点的路径转换为IF—THEN形式的分类规则,这种形式更有利于理解。
从一类无序、无规则的事物(概念)中推理出决策树表示的分类规则。
三、ID3算法问题
信息增益偏好取值多的属性(分散,极限趋近于均匀分布)
1、 属性筛选度量标准
可能会受噪声或小样本影响,易出现过拟合问题。
结果训练出来的形状是一棵庞大且深度很浅的树,这样的划分是极为不合理的。
改进方法:
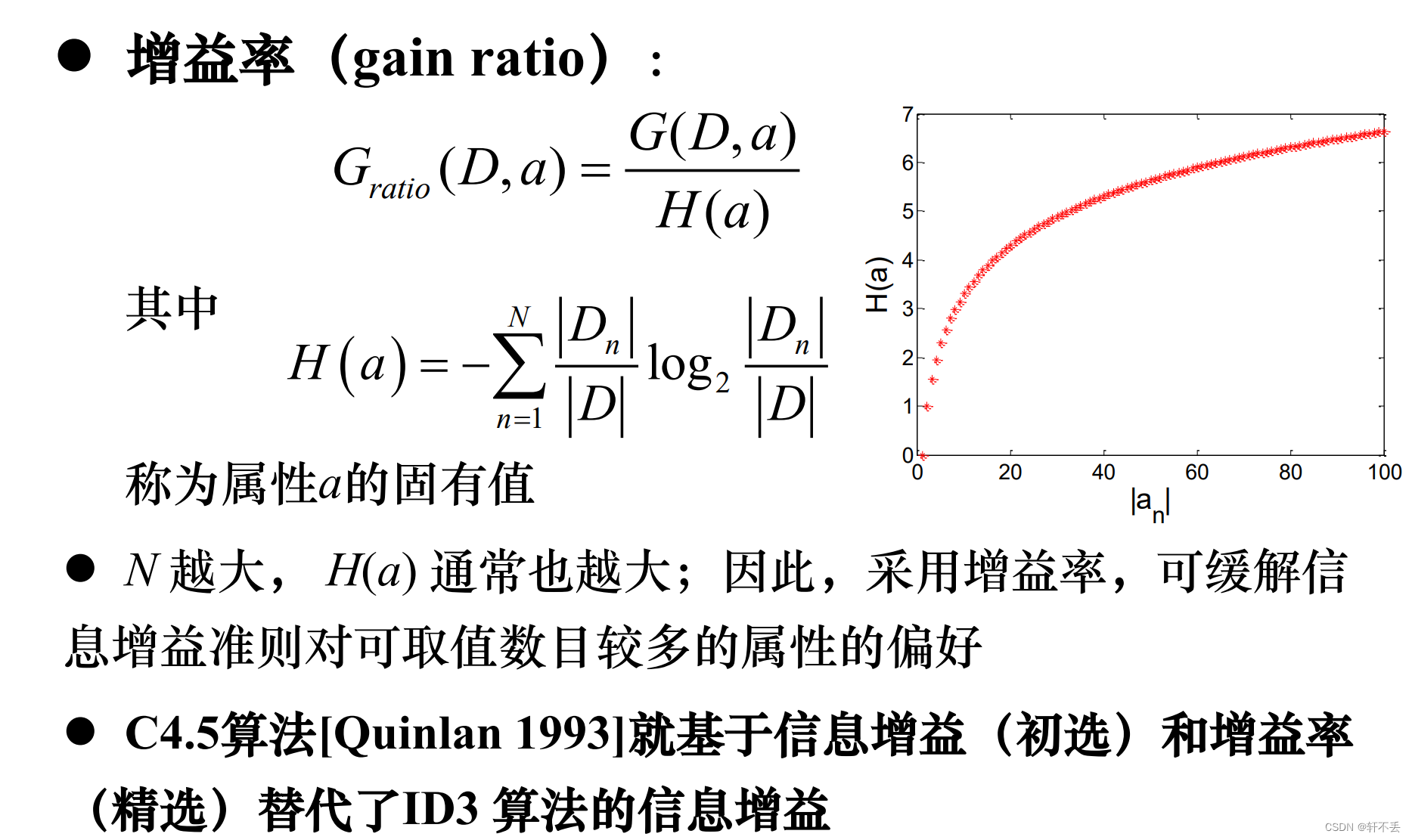

2、 剪枝处理
1)问题
无法处理连续值的属性。
决策树对训练数据有很好的分类能力,但对未知的测试数据未必有好的分类能力,泛化能力弱,即可能发生过拟合现象。
训练数据有噪声,对训练数据拟合的同时也对噪音进行拟合,影响了分类效果。
叶节点样本太少,易出现耦合的规律性,使一些属性恰巧可以很好地分类,但却与实际的目标函数并无关系。
2)解决
剪枝是决策树学习算法中对付“过拟合”的主要手段
-
预剪枝策略(pre-pruning):
决策树生成过程中,对每个节点在划分前进行估计,若划分不能带来决策树泛化性能提升,则停止划分,并将该节点设为叶节点
优点:预剪枝“剪掉了”很多没必要展开的分支,降低了过拟合的风险,并且显著减少了决策树的训练时间开销和测试时间开销
劣势:有些分支的当前划分有可能不能提高甚至降低泛化性能,但后续划分有可能提高泛化性能;预剪枝禁止这些后续分支的展开,可能会导致欠拟合 -
后剪枝策略(post-pruning):
先利用训练集生成决策树,自底向上对非叶节点进行考察,若将该叶节点对应子树替换为叶节点能带来泛化性能提升,则将该子树替换为叶节点
优点:优势:测试了所有分支,比预剪枝决策树保留了更多分支,降低了欠拟合的风险,泛化性能一般优于预剪枝决策树。
劣势:后剪枝过程在生成完全决策树后在进行,且要自底向上对所有非叶节点逐一评估;因此,决策树的训练时间开销要高于未剪枝决策树和预剪枝决策树
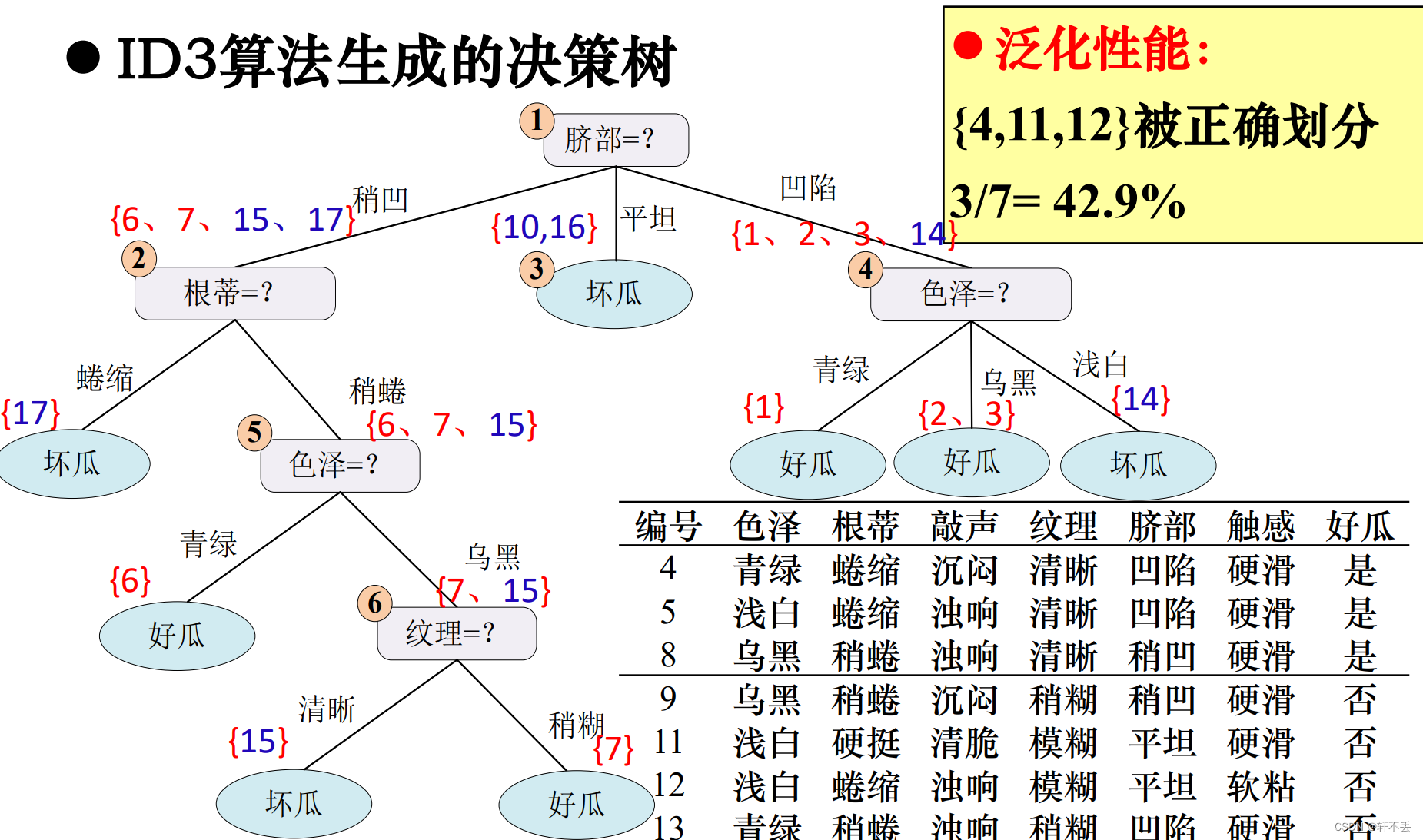
3)案例
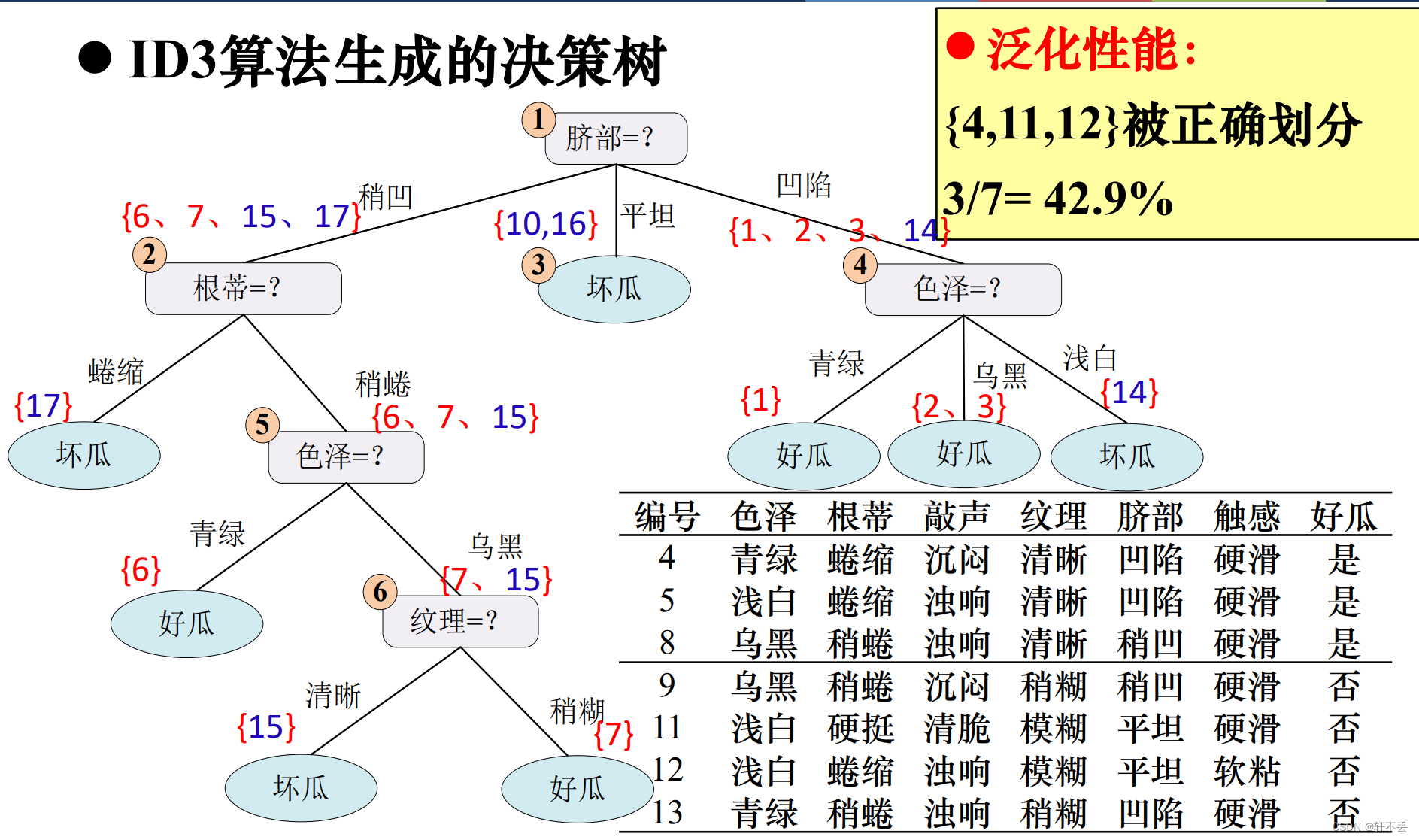
预剪枝算法


后剪枝算法





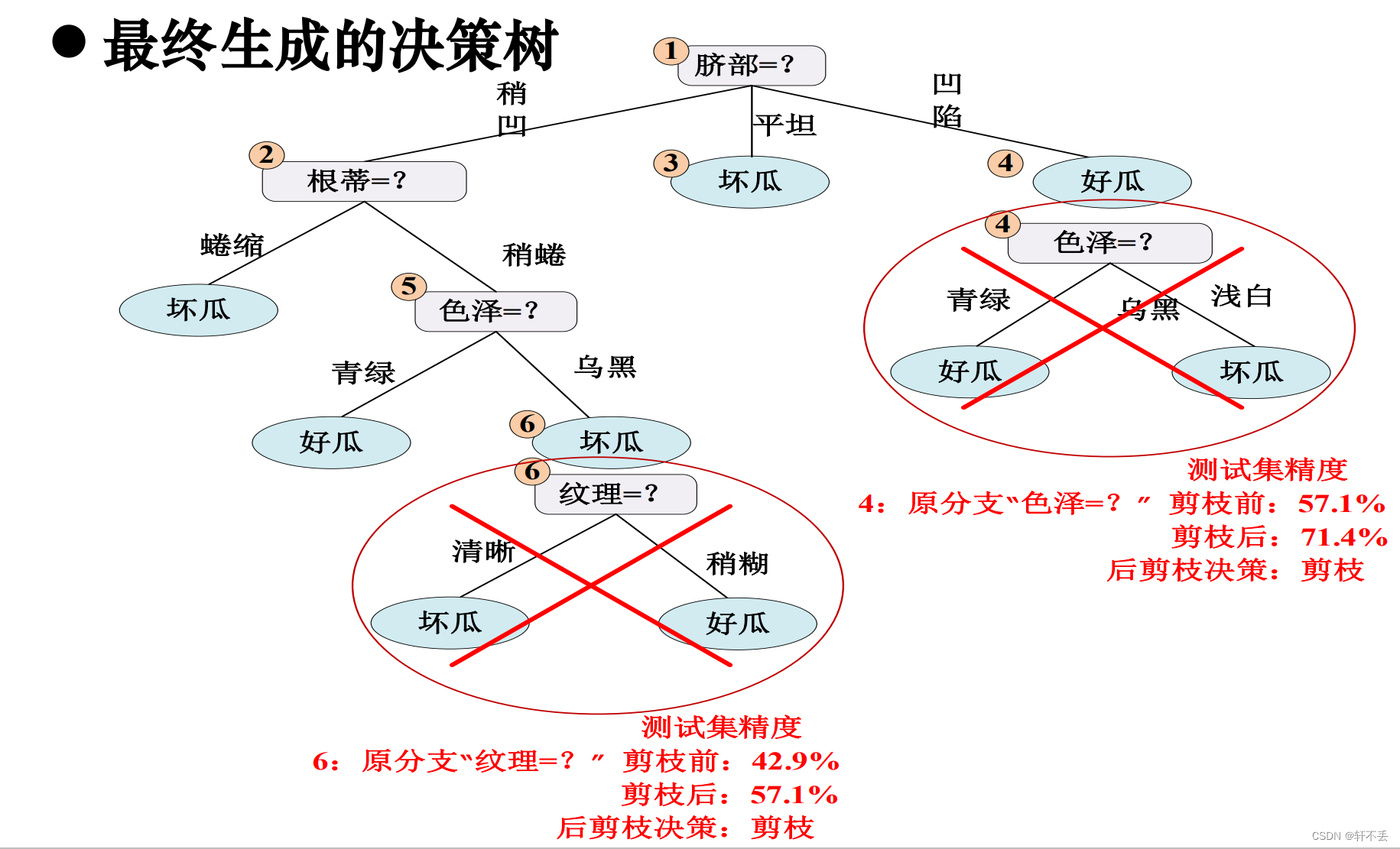
3、 连续值处理
无法处理属性值不完整的训练数据
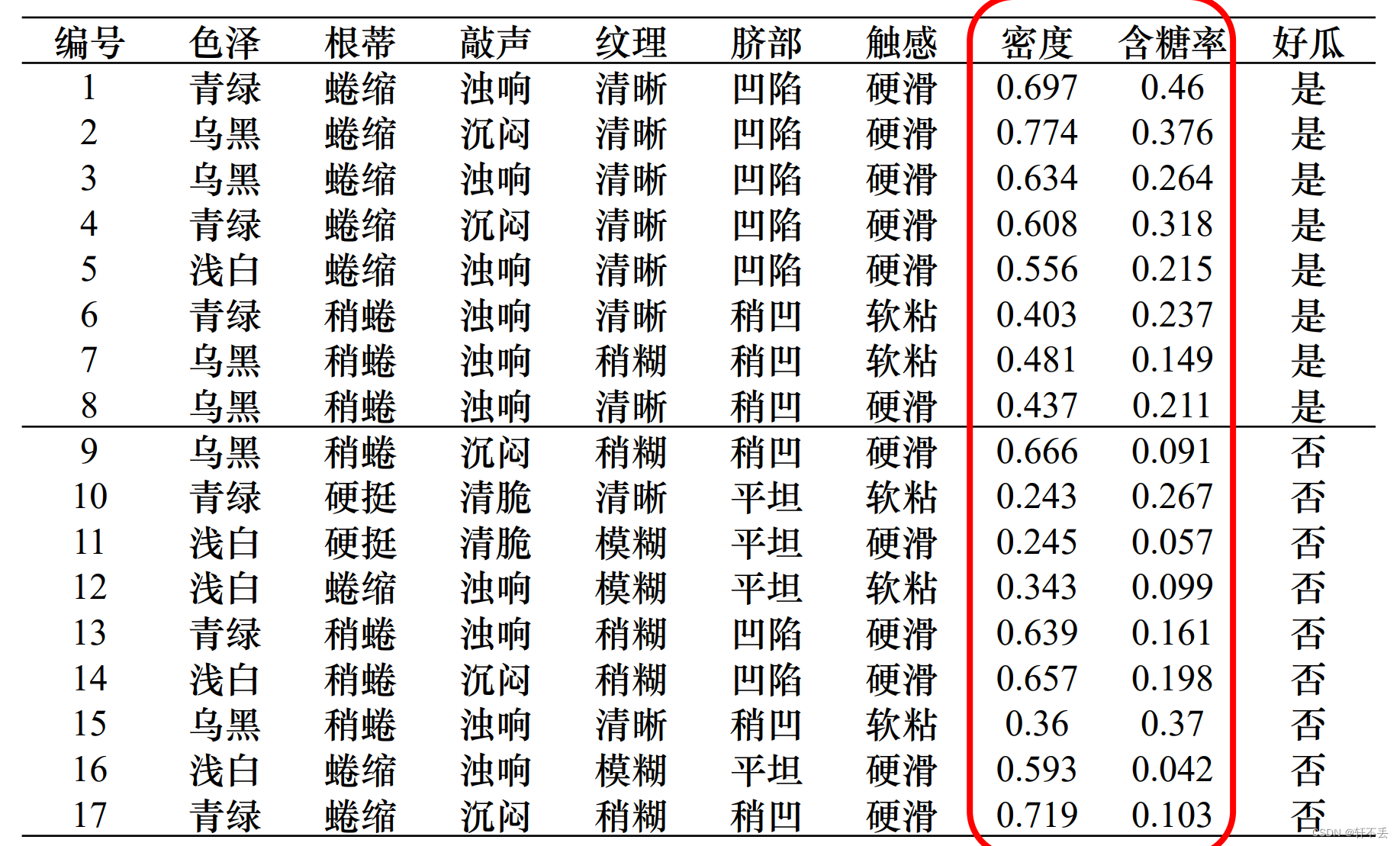
基本思想:采用二分法(bi-partition)进行离散化


4、 缺失值处理
无法处理不同代价的属性
前面假设:所有样本的属性完整
实际情况:存在不完整样本:即样本的某些属性缺失;特别是属性数目较多时
如果简单放弃不完整样本,会导致数据信息的浪费
实际中确实需要属性缺失情况下进行决策
◼ 不同代价属性的处理
需要解决的两个问题
- 如何在属性值缺失的情况下进行划分属性选择(计算信息增益)?



- 给定划分属性,若样本在该属性上的值缺失,如何对样本进行划分?

案例:
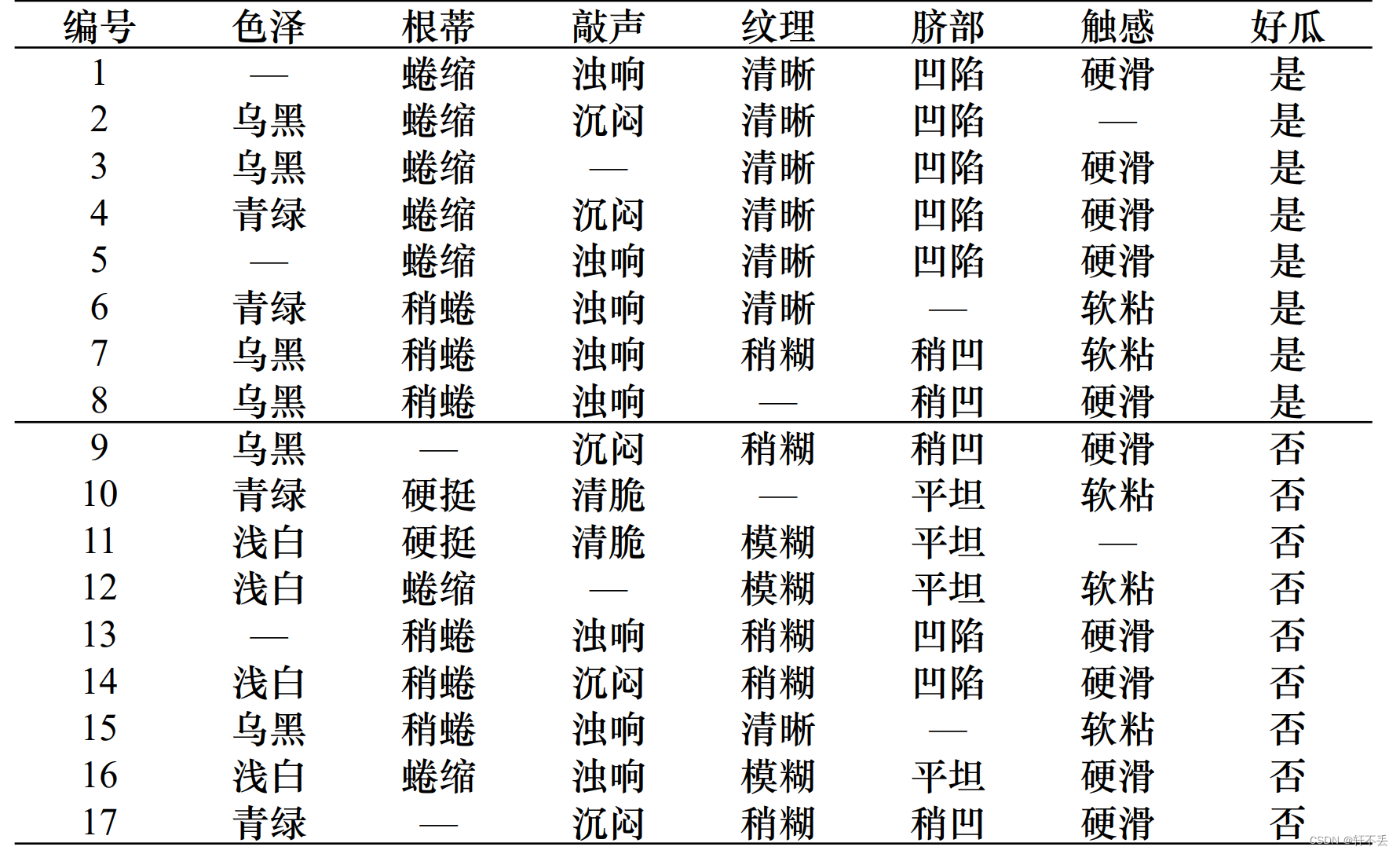



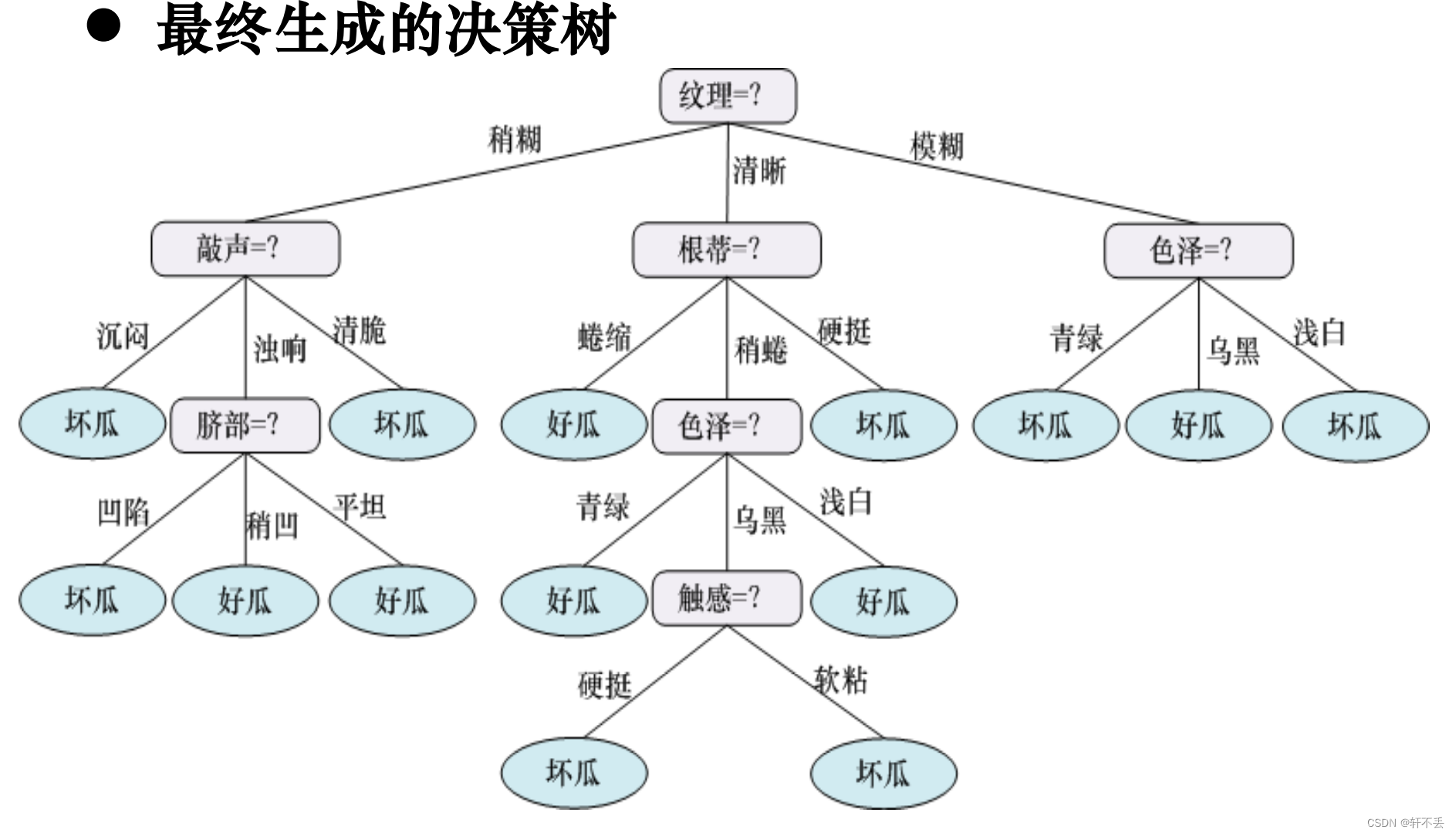
5、不同代价属性的处理
不同的属性测量具有不同的代价
在属性筛选度量标准中考虑属性的不同代价
优先选择低代价属性的决策树
必要时才依赖高代价属性