一、定义、理解
非零子式的最高阶数。
如何理解?什么叫做非零子式的最高阶数???
举个例子:有一个5阶矩阵
首先什么叫子式?
例如2阶子式就是,任取某两行某两列组成的行列式,就叫做子式
同理,3阶子式就是任取谋三行三列组成的行列式。
其次,什么叫做非零子式的最高阶数?
很好理解,例如,这个矩阵A的3阶子式均不为0
但是,A的4阶、5阶子式全都为0
那么,此时,这个矩阵A的非零子式的最高阶数就是3
但是一般来说,这种理解很抽象,也很繁杂,难道我取算一个矩阵的秩要从它的1阶、2阶...直到算出为0的n阶子式为止吗?很明显,这简直式脑子抽了。
但是,就没有办法了吗?
有。这就是初等变换。
二、初等行变换求矩阵的秩(重点)
为什么可以使用初等变换求矩阵的秩?
核心:初等变换不改变矩阵的秩
由于这个性质,A乘一个可逆矩阵B,不改变A的秩。
因为可逆矩阵可以视为一系列初等矩阵的乘积组合。
所以,我们只用初等行变换将A化成一个更简单的矩阵,来判断非零子式的最高阶。
(注意,学长标出的式行变换,而不是列变换,为什么?第一,足够化出来;第二,后期求线性防方程的基础解析会用到,基础解系是重点的重点!)
例题:
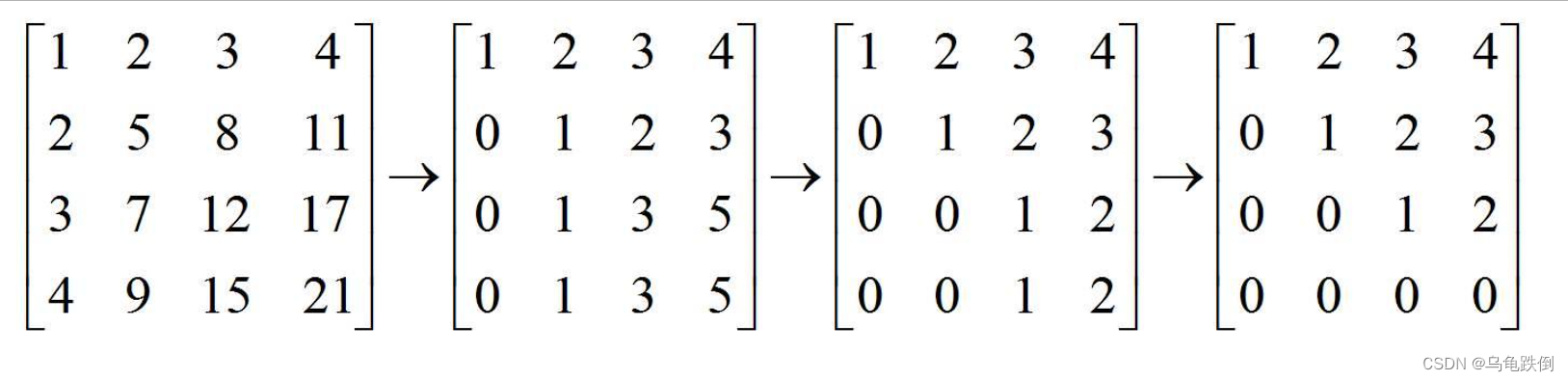
这个矩阵的秩为3,为什么?
因为最后一行为0,如果将最后一行包括进去,那么行列式就为0.
如果矩阵的秩为4,叫做满秩。