1.小美的外卖订单

简单的加法逻辑,需要注意的是各个数据的边界问题
- 折扣价不能超过原价
- 减的价格不能超过满的价格
- 满减优惠仅限原价购入
const rl = require("readline").createInterface({ input: process.stdin });
void (async function () {let count = 0;let list = [];let man = 0,jian = 0;rl.on("line", function (line) {if (count === 0) {count = parseInt(line);} else if (list.length < count) {const item = line.split(" ");list.push([parseFloat(item[0]), parseFloat(item[1])]);} else {const item = line.split(" ");man = parseFloat(item[0]);jian = parseFloat(item[1]);console.log(getPrices(list, man, jian));}});
})();function getPrices(list, man, jian) {if(jian > man || man <= 0 || jian <= 0) return 'error'let prices1 = 0,prices2 = 0;for (let i = 0; i < list.length; i++) {if (list[i][1] > list[i][0] || list[i][1] <= 0 || list[i][0] <= 0) return "error";prices1 += list[i][0];prices2 += list[i][1];}if (prices1 >= man) {prices1 -= jian;}return prices1 > prices2 ? prices2.toFixed(2) : prices1.toFixed(2);
}2.小美的字符串匹配度

- 第一步计算s和t中不操作的匹配度,也就是s[i] === t[i] 的个数
- 第二步,计算对t操作一次能增加的匹配的
const rl = require("readline").createInterface({ input: process.stdin });void async function () {let length = 0;let s = '',t = '';// Write your code hererl.on('line',function(line){if(length === 0) {length = parseInt(line)} else if(s === '') {s = line;} else {t = line;console.log(computed(s,t))}})
}()
function computed(s, t) {//计算原本的匹配度let baseCount = 0;//记录无需交换操作的下标let used = new Array(s.length).fill(false);for (let i = 0; i < s.length; i++) {if (s[i] == t[i]) {used[i] = true;baseCount++;}}//计算操作一次增加的匹配度 1 or 2let changeCount = 0;for (let i = 1; i < t.length; i++) {//原本就匹配的,无需交换if (used[i]) continue;for (let j = i + 1; j < s.length; j++) {//原本就匹配的,无需交换if (used[j]) continue;// 满足交换后一个相等 继续执行// 满足两个相等,直接返回,操作一次最多怎加两个pipeiduif (t[i] === s[j]) {changeCount = 1;if (t[j] === s[i]) {return baseCount + 2;}}}}return baseCount + changeCount;
}3.小美的树上染色

贪心算法: 最优解就是从每条路径的叶子节点开始染红
const rl = require("readline").createInterface({ input: process.stdin });
let nodeValue = [];
let edgeMap = new Map()
void async function () {let start = 0;let nodeCount = 0;rl.on('line',function(line) {if(nodeCount === 0) {nodeCount = parseInt(line);} else if(nodeValue.length === 0) {nodeValue = line.split(' ').map(_ => parseInt(_))} else {start++;const item = line.split(' ')edgeMap.set(item[0],[...(edgeMap.get(item[0]) || []),item[1]])if(start == nodeCount - 1) {let hasVisited = []dfs('1',hasVisited);console.log(hasVisited.length)}}})
}()function dfs(u,hasVisited) {//循环可到达if(edgeMap.has(u)) {for(let x of edgeMap.get(u)) {dfs(x,hasVisited);//遍历到每条线的末尾,叶子节点if(Math.sqrt(nodeValue[x-1] * nodeValue[u - 1]) % 1 === 0 && !hasVisited.includes(x) && !hasVisited.includes(u)) {hasVisited.push(x);hasVisited.push(u);}}}
}4.小美的排列询问

简单无脑过: 找到x的位置,如果在x前后找到y就是yes
const rl = require("readline").createInterface({ input: process.stdin });void (async function () {let nodeCount = 0;let list = [];let x = null,y = null;rl.on("line", function (line) {if (nodeCount === 0) {nodeCount = parseInt(line);} else if (list.length === 0) {list = line.split(" ");} else {[x, y] = line.split(" ");let flag = "No";for (let i = 0; i < nodeCount - 1; i++) {if ((list[i] == x && list[i + 1] == y) ||(list[i] == y && list[i + 1] == x)) {flag = "Yes";break;}}console.log(flag);}});
})();
5.小美的排列构造

要让相邻两项的和的差值最小,排列需要满足第一大挨着第一小,第二大挨着第二小。例如n=6,满足要求的排列可以是[6,1,5,2,4,3],也可以是[1,6,2,5,3,4],权值都是0
题外话: n为偶数,权值为0,n为奇数,权值为 Math.ceil(n / 2)
const rl = require("readline").createInterface({ input: process.stdin });void (async function () {let count = 0;rl.on("line", function (line) {if (count === 0) {count = parseInt(line);let list = "";let i = 1,j = count;while (i < j) {list = list + i + " " + j + " ";j--;i++;}if (count % 2 === 1) {list += j;}console.log(list.trimEnd());}});
})();
6.小美走公路

公路是环形的,可以顺时针走,也可以逆时针走,要求最短距离。
设x到y的直线距离是distanceA,从任意点顺时针走一圈的距离是distanceB, distanceB-distanceA代表x到y的绕圈距离,答案就是distanceA和distanceB-distanceA的最小值
const rl = require("readline").createInterface({ input: process.stdin });void (async function () {let stationCount = 0;let distance = [];let start = 0,end = 0;rl.on("line", function (line) {if (stationCount === 0) {stationCount = parseInt(line);} else if (distance.length === 0) {distance = line.split(" ").map((_) => parseInt(_));} else {[start, end] = line.split(" ").map((_) => parseInt(_));console.log(getDistance(distance, start, end));}});
})();function getDistance(distance, start, end) {//跑一圈 a点到a点const oneCircle = distance.reduce((total, cur) => total + cur, 0);//记录距离let total = 0;if (start > end) {//直线距离[start, end] = [end, start];}for (let i = start; i < end; i++) {total += distance[i - 1];}//直线距离 ? 还是绕一圈 ?return Math.min(total, oneCircle - total);
}
7.小美的好矩阵

直接遍历矩阵,然后判定
const rl = require("readline").createInterface({ input: process.stdin });void (async function () {let n = 0,m = 0;let matrix = [];rl.on("line", function (line) {if (n == 0) {const item = line.split(" ");n = parseInt(item[0]);m = parseInt(item[1]);} else {matrix.push(line.split(""));if (matrix.length === n) {console.log(getButyNum(matrix, n, m));}}});
})();
function getButyNum(matrix, n, m) {let count = 0;if (n < 3 || m < 3) return count;for (let i = 0; i <= n - 3; i++) {for (let j = 0; j <= m - 3; j++) {if (isButy(matrix, i, j)) {count++;}}}return count;
}
function isButy(matrix, p, q) {let a = false,b = false,c = false;for (let i = p; i < p + 3; i++) {for (let j = q; j < q + 3; j++) {if (matrix[i][j] === "A") {a = true;} else if (matrix[i][j] === "B") {b = true;} else if (matrix[i][j] === "C") {c = true;} else {return false;}if (i - 1 >= p && matrix[i][j] === matrix[i - 1][j]) {return false;}if (i + 1 < p + 3 && matrix[i][j] === matrix[i + 1][j]) {return false;}if (j - 1 >= q && matrix[i][j] === matrix[i][j - 1]) {return false;}if (j + 1 < q + 3 && matrix[i][j] === matrix[i][j + 1]) {return false;}}}return a && b && c;
}
8.小美的蛋糕切割
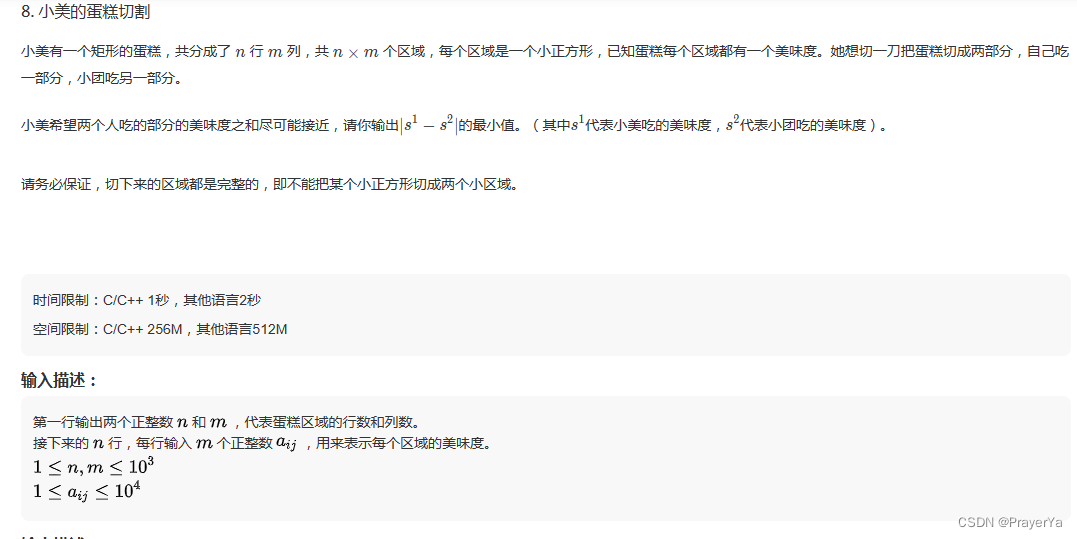
由于不能把某个小正方形切成两个区域,所有的切法就是n-1种沿着行切开和m-1种沿着列切开,分别计算n+m-2种美味度的差值,取最小值
const rl = require("readline").createInterface({ input: process.stdin });void async function () {let n = 0,m = 0;let matrix = [];rl.on('line',function(line) {if(n == 0) {const item = line.split(" ")n = parseInt(item[0])m = parseInt(item[1])} else {matrix.push(line.split(" "));if(matrix.length === n) {console.log(getMiniDiff(matrix, n, m));}}})
}()
function getMiniDiff(matrix, n, m) {//分别计算每行每列美味值,以及整个蛋糕的美味值let rows = new Array(n).fill(0);let columns = new Array(m).fill(0);let total = 0;for(let i=0;i<n;i++) {for(let j=0;j<m;j++) {const value = parseInt( matrix[i][j])rows[i] += valuecolumns[j] += valuetotal += value}}let diff = total;//查询按照行切割,美味差值let sum = 0;for(let i=0;i<rows.length;i++) {sum += rows[i];diff = Math.min(diff,Math.abs(2*sum - total))}//查询按照列切割,美味差值sum = 0;for(let j=0;j<columns.length;j++) {sum+=columns[j];diff = Math.min(diff,Math.abs(2*sum - total))}//return diff
}
9.小美的字符串变换

先暴力算出满足要求的矩阵的x,y组合,再挨个计算出每种矩阵的连通块数量(深度遍历dfs),取最小值
const rl = require("readline").createInterface({ input: process.stdin });void (async function () {let count = 0;rl.on("line", function (line) {if (count === 0) {count = parseInt(line);} else {console.log(getBlocks(count, line));}});
})();
function getBlocks(count, str) {//计算可能x y组合let group = [];for (let i = 1; i <= count; i++) {for (let j = 1; j <= count; j++) {if (i * j == count) {group.push([i, j]);}}}//分别计算矩阵let result = str.length;for (let k = 0; k < group.length; k++) {const x = group[k][0];const y = group[k][1];let temp = 0;//记录当前矩阵连通块数量let list = str.split("");for (let i = 0; i < x; i++) {for (let j = 0; j < y; j++) {if (list[i * y + j] !== "0") {temp++;dfs(x, y, list, i, j, list[i * y + j]);}}}result = Math.min(result, temp);}return result;
}
function dfs(x, y, list, i, j, flag) {//判定i,j合法性if (!(i >= 0 && i < x && j >= 0 && j < y)) {return;}//不和参考相等就退出if (list[i * y + j] != flag) {return;}//当前重置为0,再向上下左右拓展list[i * y + j] = "0";dfs(x, y, list, i - 1, j, flag);dfs(x, y, list, i + 1, j, flag);dfs(x, y, list, i, j - 1, flag);dfs(x, y, list, i, j + 1, flag);
}
总结: 稍微难一点的是3题和9题,需要对【贪心算法+图+深度优先算法】有一些了解,其余的都是考验基本编程能力和动点小脑筋的题目(考察透过题目直击根本逻辑的能力)。
不足:虽然都做出来了,但是耗时太长。大概是有做题恐惧症>.< ,一想到自己在做题,脑袋就不能思考了,一旦停止考试,脑袋就工作正常了。害,还是经历的少了,多做几套大概就好了。