1.傅里叶处理图片原理和代码实现-编程知识

在这里首先声明，本文纯粹看了别的博主的文章，觉得博主写的原理清晰明了，容易理解，很详细，在这里写一遍是作为笔记，方便以后再翻看时容易查找。大家可以参考下面这个博文：

图像的傅里叶变换_图像傅里叶变换-CSDN博客，若觉得抄袭，可以提醒我删了，这里只是记笔记，没有其他目的。

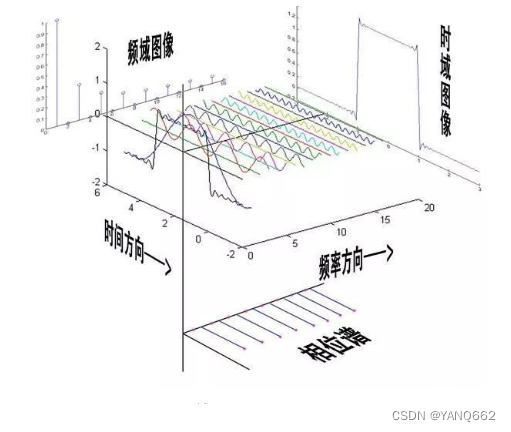
傅里叶基础

法国数学家吉恩·巴普提斯特·约瑟夫·傅里叶被世人铭记的最大的贡献是：他指出任何周期函数都可以表示为不同频率的正弦和/或余弦之和的形式，每个正弦项和/或余弦项乘以不同的系数（现在称该和为傅里叶级数）。无论函数多么复杂，只要它是周期的，并且满足某些适度的数学条件，都可以用这样的和来表示。即一个复杂的函数可以表示为简单的正弦和余弦之和。甚至非周期函数（单该曲线下的面积是有限的）也可以用正弦和/或余弦乘以加权函数的积分来表示。在这种情况下的公式就是傅里叶公式。 whaosoft aiot http://143ai.com

比如说我们以制作一个饮料的过程，使用时域的角度来看就是这样：

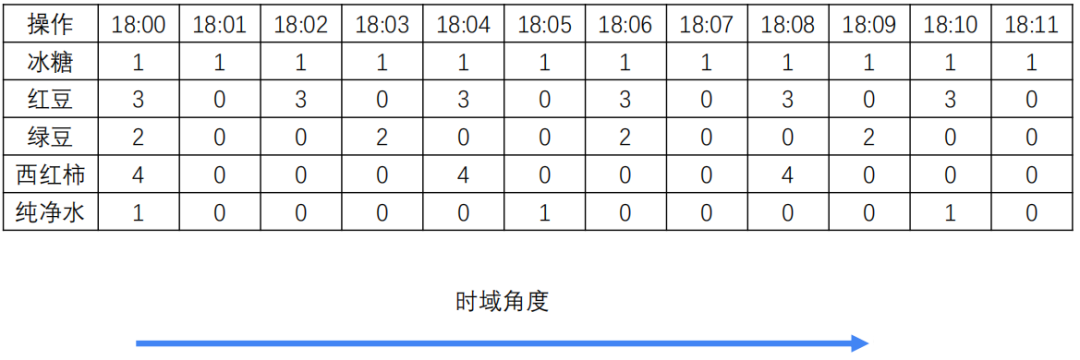
这里是什么意思呢，就是说一个饮料的制作需要在18点整放1个单位冰糖、3个单位红豆、2个单位的绿豆、4个单位的西红柿，还有1个单位的纯净水。然后再18：01分只需要假如一个单位的纯净水。后面也是一致。
而频域是怎么描述这件事的呢？

具体来说就是说他发现了一个规律，就是说这个制作过程，每分钟都要加入冰糖，每两分钟都要加入红豆，每三分钟都要加入一次绿豆…

对于时域角度我们这样描述。

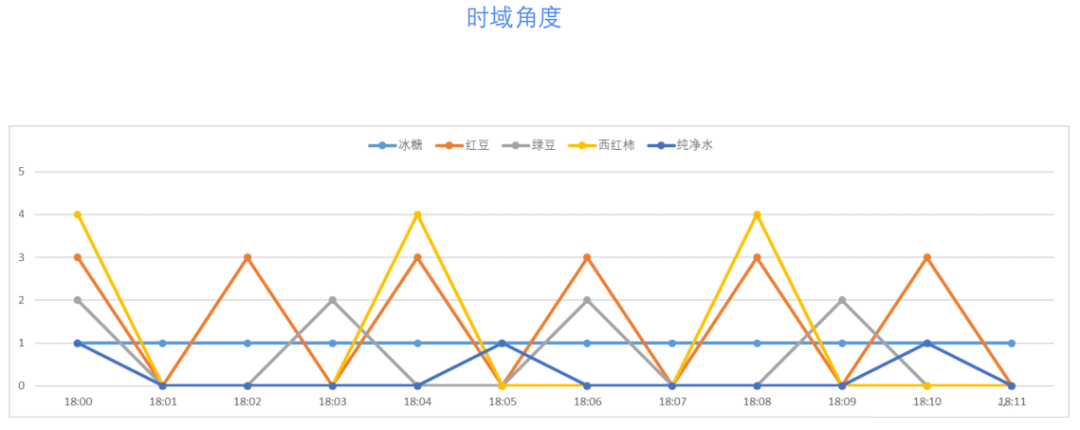
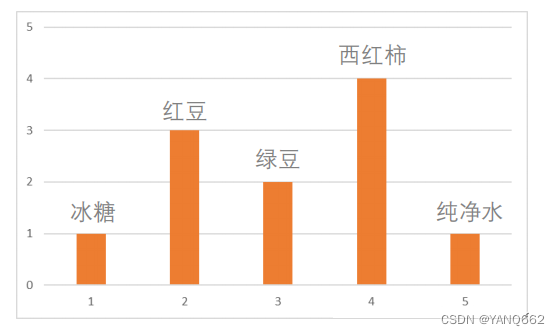
对于频域角度我们这样描述这件事，用直方图表示就是：

如果要考虑更精准的时间精度，我们就要引入相位这个概念，它是一个和时间差有关的一个表述。

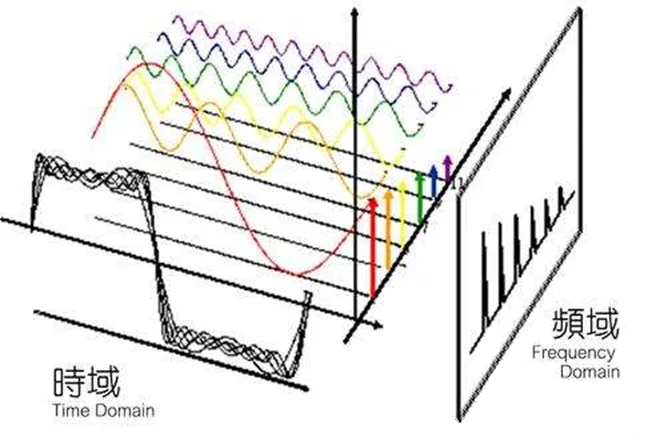
这里我们说明一下就是时域和频域的表述是互逆的，对于时域我们是时间为横坐标，振幅为纵坐标。对于频域我们以频率为横坐标，振幅为纵坐标。但是可以看得出来频域的表述更加简单，但是比较抽象，不容易理解。

傅里叶说：任何连续周期信号，可以由一组适当的正弦曲线组合而成。

注意这里是一组而不是一个。比如对于这样的一个图像：

f(x)=3np.sin(0.8x)+7np.sin(1/3x)+2np.sin(0.2x)

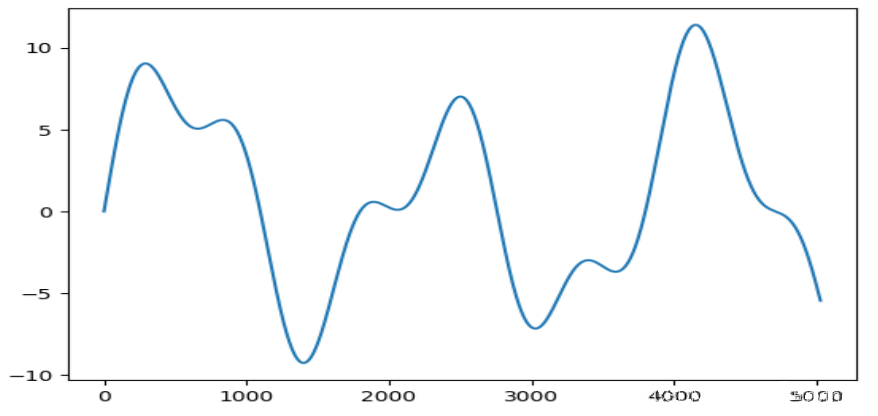
看上去是毫无规律可言吧，但是它也可以由一组正弦函数组成。

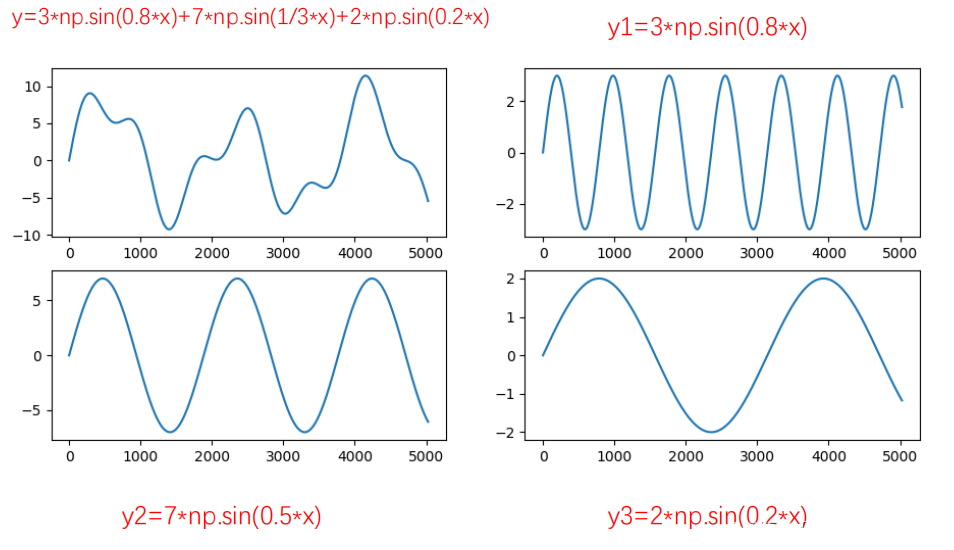
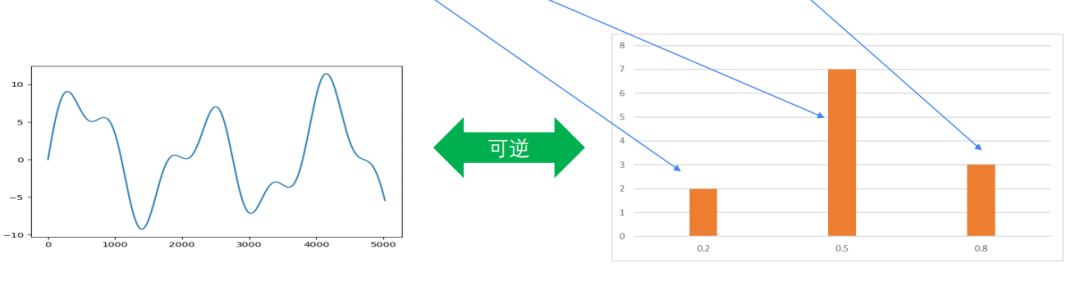
他们是可逆的，想不到吧，乱七八糟的东西也有规律了。但是他们就是这样组合而成的吗？不可能吧，所以这里就是不是同时开始的一组余弦函数，在叠加时要体现开始的时间。也就说组合的函数他们的开始时间是不一样的。在这里分别对应0，2，3，看公式就看出来啦。

这里多说一嘴就是傅里叶变换从时域角度来看，这个世界是动态的！从频域角度来看这个世界是静止的。

从数学角度来讲：傅里叶变换将一个任意的周期函数分解成为无穷个正弦函数的和的形式。

从物理角度来讲：傅里叶变换实现了将信号从空间域到频率域的转换。

傅里叶基础numpy实现

python是可以实现傅里叶变换的，这里就要说到三剑客的numpy了。对应的函数是：numpy.fft.fft2返回一个复数数组(complex ndarray)。numpy.fft.fftshift这个函数时表示把将零频率分量移到频谱中心。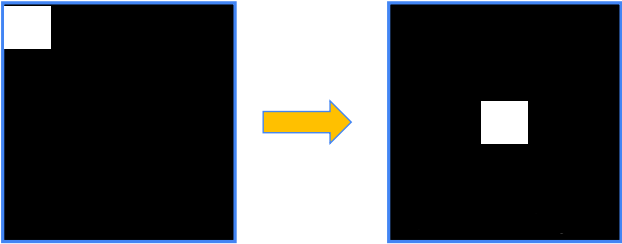

还要设置频谱的范围20*np.log(np.abs(fshift))，对于图像来说就是255了。

import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('image\\lena.bmp',0)
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
result = 20*np.log(np.abs(fshift))
plt.subplot(121)
plt.imshow(img, cmap = 'gray')
plt.title('original')
plt.axis('off')
plt.subplot(122)
plt.imshow(result, cmap = 'gray')
plt.title('result')
plt.axis('off')
plt.show()

结果是：

原图和频谱图像。

傅里叶得到低频、高频信息，针对低频、高频处理能够实现不同的目的。
傅里叶过程是可逆的，图像经过傅里叶变换、逆傅里叶变换后，能够恢复到原始图像。
在频域对图像进行处理，在频域的处理会反映在逆变换图像上。

逆傅里叶numpy实现

对于傅里叶的逆操作这里没有什么可说的，就是把频域图像转回原图像。

函数是：numpy.fft.ifft2，那么还有一个操作就是把中间移动回去。numpy.fft.ifftshift。

iimg = np.abs(逆傅里叶变换结果)而第二个图就表示低频部分，边缘就表示为高频部分。

import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('image\\boat.bmp',0)
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
ishift = np.fft.ifftshift(fshift)
iimg = np.fft.ifft2(ishift)
iimg = np.abs(iimg)
plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('original'),plt.axis('off')
plt.subplot(122),plt.imshow(iimg, cmap = 'gray')
plt.title('iimg'),plt.axis('off')
plt.show()

首先我们要进行傅里叶变换，才可以进行逆操作。结果是：

完全一致！！！

频域的高通滤波

首先我们来看看到底什么是高频，什么是低频，在图像中如何理解。

低频对应图像内变化缓慢的灰度分量。例如，在一幅大草原的图像中，低频对应着广袤的颜色趋于一致的草原。

高频对应图像内变化越来越快的灰度分量，是由灰度的尖锐过渡造成的。例如，在一幅大草原的图像中，其中狮子的边缘等信息。

对于滤波我们之前也了解过了，就是说过滤掉不需要的部分。

通过低频的滤波器称为低通滤波器。

通过高频的滤波器称为高通滤波器。

修改傅里叶变换以达到特殊目的，然后计算IDFT返回到图像域。比如我们可以利用傅里叶变换进行，图像增强、图像去噪、边缘检测、特征提取、图像压缩、图像加密等。

衰减高频而通过低频，低通滤波器，将模糊一幅图像。

衰减低频而通过高频，高通滤波器，将增强尖锐的细节，但是会导致图像的对比度降低。

那么我们只需要再滤波中来一个掩膜操作，具体看下面：

对于这个掩膜我们这样做：

rows, cols = img.shape
crow,ccol = int(rows/2) , int(cols/2)
fshift[crow-30:crow+30, ccol-30:ccol+30] = 0

具体代码是：

import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('image\\boat.bmp',0)
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
rows, cols = img.shape
crow,ccol = int(rows/2) , int(cols/2)
fshift[crow-30:crow+30, ccol-30:ccol+30] = 0
ishift = np.fft.ifftshift(fshift)
iimg = np.fft.ifft2(ishift)
iimg = np.abs(iimg)
plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('original'),plt.axis('off')
plt.subplot(122),plt.imshow(iimg, cmap = 'gray')
plt.title('iimg'),plt.axis('off')
plt.show()

得到后的图象是这样的：

可以出来把边缘描绘的非常完整，但是图像的对比度降低了。

傅里叶OpenCV实现

对于OpenCV中的傅里叶变换函数是：返回结果=cv2.dft(原始图像，转换标识)

返回结果是双通道的，第一个是实数部分，第二个通道是虚数部分。

输入图像要首先转换成np.float32格式，np.float32(img)

flags = cv2.DFT_COMPLEX_OUTPUT，输出一个复数阵列

移动频谱部分和numpy一致，是这样的，numpy.fft.fftshift，然后进行返回值=cv2.magnitude(参数1，参数2)，这里参数1就是实数部分，参数2就是虚数部分，并且进行𝑑𝑠𝑡 𝐼 = 根号𝑥(𝐼)2 + 𝑦(𝐼)2操作。

import numpy as np
import cv2
import matplotlib.pyplot as plt
img = cv2.imread('image\\lena.bmp',0)
dft = cv2.dft(np.float32(img),flags = cv2.DFT_COMPLEX_OUTPUT)
dftShift = np.fft.fftshift(dft)
result = 20*np.log(cv2.magnitude(dftShift[:,:,0],dftShift[:,:,1]))
plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('original'),plt.axis('off')
plt.subplot(122),plt.imshow(result, cmap = 'gray')
plt.title('result'), plt.axis('off')
plt.show()

得到的图像和numpy一致。

傅里叶OpenCV逆变换实现

对于傅里叶变换的逆操作，使用OpenCV的函数就是返回结果=cv2.idft(原始数据)，然后计算幅度函数仍然是返回值=cv2.magnitude(参数1，参数2)，numpy.fft.ifftshift

import numpy as np
import cv2
import matplotlib.pyplot as plt
img = cv2.imread('image\\lena.bmp',0)
dft = cv2.dft(np.float32(img),flags = cv2.DFT_COMPLEX_OUTPUT)
dftShift = np.fft.fftshift(dft)
ishift = np.fft.ifftshift(dftShift)
iImg = cv2.idft(ishift)
iImg= cv2.magnitude(iImg[:,:,0],iImg[:,:,1])
plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('original'), plt.axis('off')
plt.subplot(122),plt.imshow(iImg, cmap = 'gray')
plt.title('inverse'), plt.axis('off')
plt.show()

频域的低通滤波

我们这里的想法就是：

自己构建一个低通滤波器，把中间位置设置成255，其余部分为0。那么我们做一个与操作，就可以把高频过滤了。

rows, cols = img.shape
crow,ccol = int(rows/2) , int(cols/2)
mask = np.zeros((rows,cols,2),np.uint8)
mask[crow-30:crow+30, ccol-30:ccol+30] = 1

低通滤波器构建代码。
然后我们完整代码就是：

import numpy as np
import cv2
import matplotlib.pyplot as plt
img = cv2.imread('image\\lena.bmp',0)
dft = cv2.dft(np.float32(img),flags = cv2.DFT_COMPLEX_OUTPUT)
dftShift = np.fft.fftshift(dft)
rows, cols = img.shape
crow,ccol = int(rows/2) , int(cols/2)
mask = np.zeros((rows,cols,2),np.uint8)
mask[crow-30:crow+30, ccol-30:ccol+30] = 1
fShift = dftShift*mask
ishift = np.fft.ifftshift(fShift)
iImg = cv2.idft(ishift)
iImg= cv2.magnitude(iImg[:,:,0],iImg[:,:,1])
plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('original'), plt.axis('off')
plt.subplot(122),plt.imshow(iImg, cmap = 'gray')
plt.title('inverse'), plt.axis('off')
plt.show()

结果是：

傅里叶变换有什么应用场景

傅里叶变换可以将一个时域信号转换成在不同频率下对应的振幅及相位，其频谱就是时域信号在频域下的表现，而反傅里叶变换可以将频谱再转换回时域的信号。最简单最直接的应用就是时频域转换，比如在移动通信的LTE系统中，要把接收的信号从时域变成频域，就需要使用FFT（快速傅里叶变换）。又例如对一个采集到的声音做傅立叶变化就能分出好几个频率的信号。比如南非世界杯时，南非人吹的呜呜主拉的声音太吵了，那么对现场的音频做傅立叶变化（当然是对声音的数据做），会得到一个展开式，然后找出呜呜主拉的特征频率，去掉展开式中的那个频率的sin函数，再还原数据，就得到了没有呜呜主拉的嗡嗡声的现场声音。而对图片的数据做傅立叶，然后增大高频信号的系数就可以提高图像的对比度。同样，相机自动对焦就是通过找图像的高频分量最大的时候，就是对好了。
————————————————
版权声明：本文为CSDN博主「whaosoft143」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_29788741/article/details/126414345