🚀前言

大家好啊！本文阿辉讲介绍插入排序和希尔排序，并将解释为什么希尔排序比插入排序更快。

🚀插入排序（insertsort）

✈️原理

插入排序，实际上是我们平时都使用过的排序，为什么这么说呢😆？想必大家都玩过扑克牌吧，大家是如何整理手中的牌的呢？一定是想下面这样对吧👇

没错，插入排序也是的么实现的

其实关于插入排序，一句话足以概括：对于要排序的数据，从前往后遍历所有数据，遍历到的数据与之前的数据进行比较，以升序为例，若遍历位置的数据比前一个数据小两者就交换，然后接着与前一个位置比较如果还小就继续交换，直到比前一个数据大就停止交换
给铁子们上动图😘

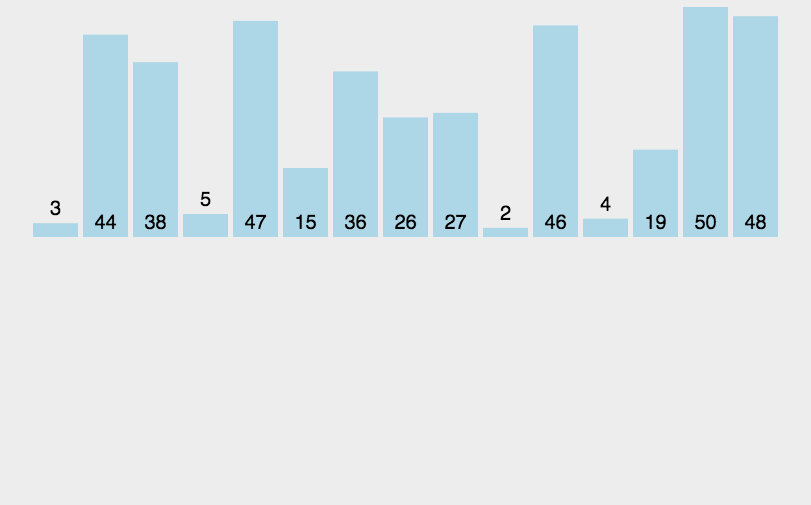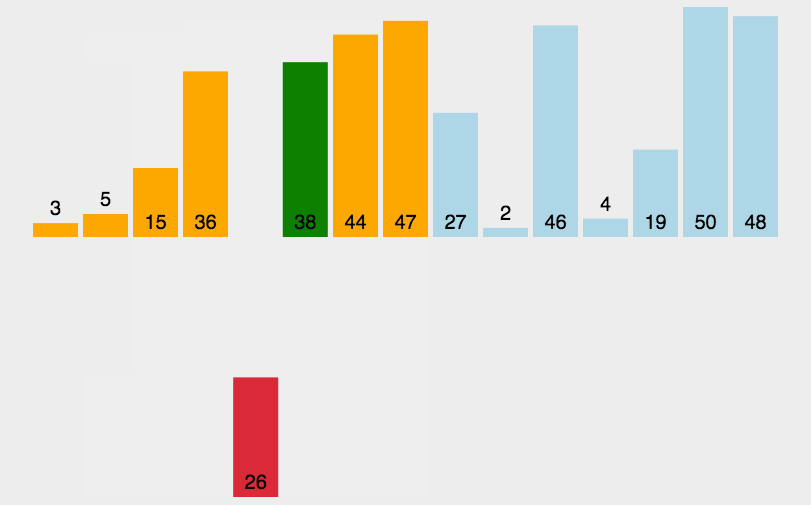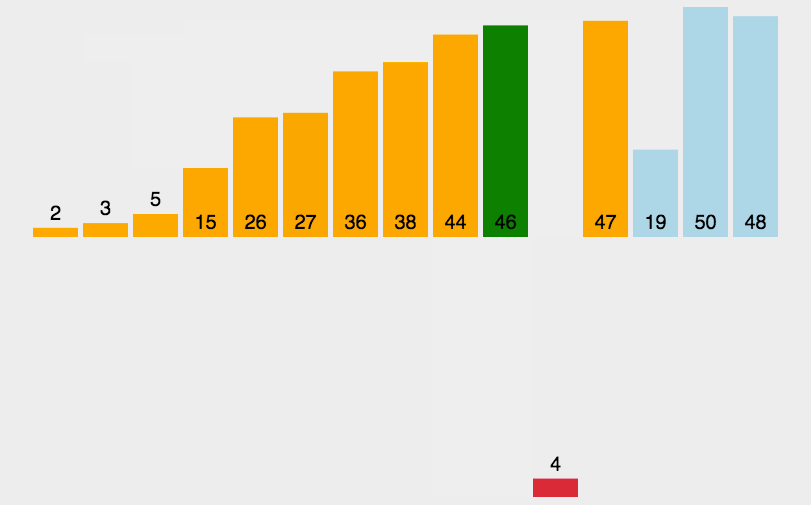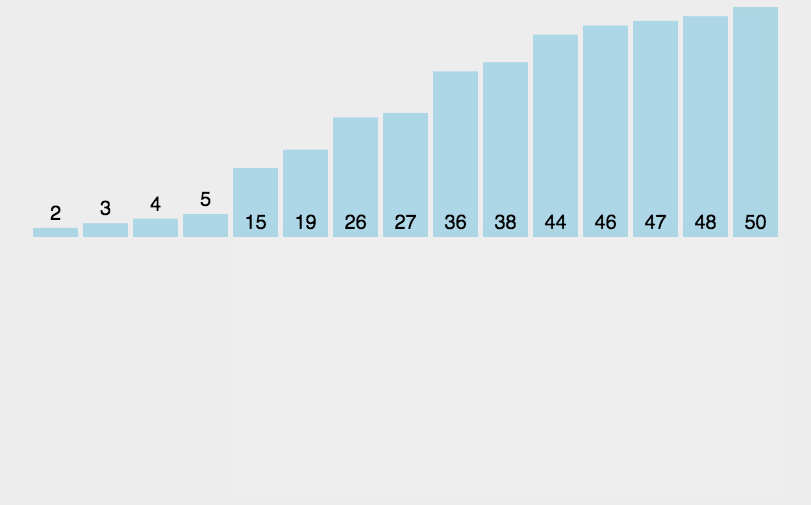
✈️代码实现（coding）

对于插入排序，我们需要两个循环来控制，一个循环来遍历所有数据，另  一个循环用来遍历已排好序的部分与要插入数据比较

coding

void insertsort(int arr[],int sz){int insert = 0;//遍历要插入的位置for(insert = 1;insert < sz;insert++){int cur = insert;//记录待排序的位置int pre = cur - 1;//记录待排序的前一个位置while(cur < pre && cur > 0){//没前一个位置大就交换，待排序位置来到0位置就退出循环int tmp = arr[cur];arr[cur] = arr[pre];arr[pre] = tmp;--cur,--pre;//待排序位置和前一个位置同时--}}
}

🚀总结

稳定性的定义

说到稳定性，与之对应就是不稳定性，那么排序算法的稳定性又为何意呢？通俗地讲就是，能保证排序前两个相等的数其在序列的前后位置顺序与排序后它们的前后位置顺序一致。形式化解释如下：一列数中，如果Ai = Aj，Ai位于Aj的前置位，那么经过升降序排序后Ai仍然位于Aj的前置位

阿辉之前介绍的 冒泡和选择排序和今天的插入排序，到现在排序中三个最挫的排序已经介绍完了，这三个的时间复杂度都是O(n²),选择排序是最挫的，冒泡和插入排序都可以做到有稳定性而选择排序做不到

为什么选择排序不行，一个简单的例子就能解释
比如一串数字 83482，一趟选择下来，第一个8与2交换，这样第一个8和第二个8之间的稳定性就被打破了

🚀希尔排序（shellsort）

希尔排序（Shell Sort）是一种基于插入排序的排序算法，也被称为“缩小增量排序”（Diminishing Increment Sort）。它通过将整个列表分割成多个较小的子序列，并对这些子序列进行插入排序，从而逐步减少排序的范围，最终完成整个列表的排序。希尔排序在提供了一种平衡了性能和简单性的排序方法。

好吧上面百度粘的说得不是人话

其实希尔排序就是将数据分组，在每个组内进行插入排序（对就是直接进行插入排序），那么如何分组呢？设置一个增量序列，开始的增量通常是数组长度的一半，然后下一次增量减半，增量设为gap，给铁子们上图

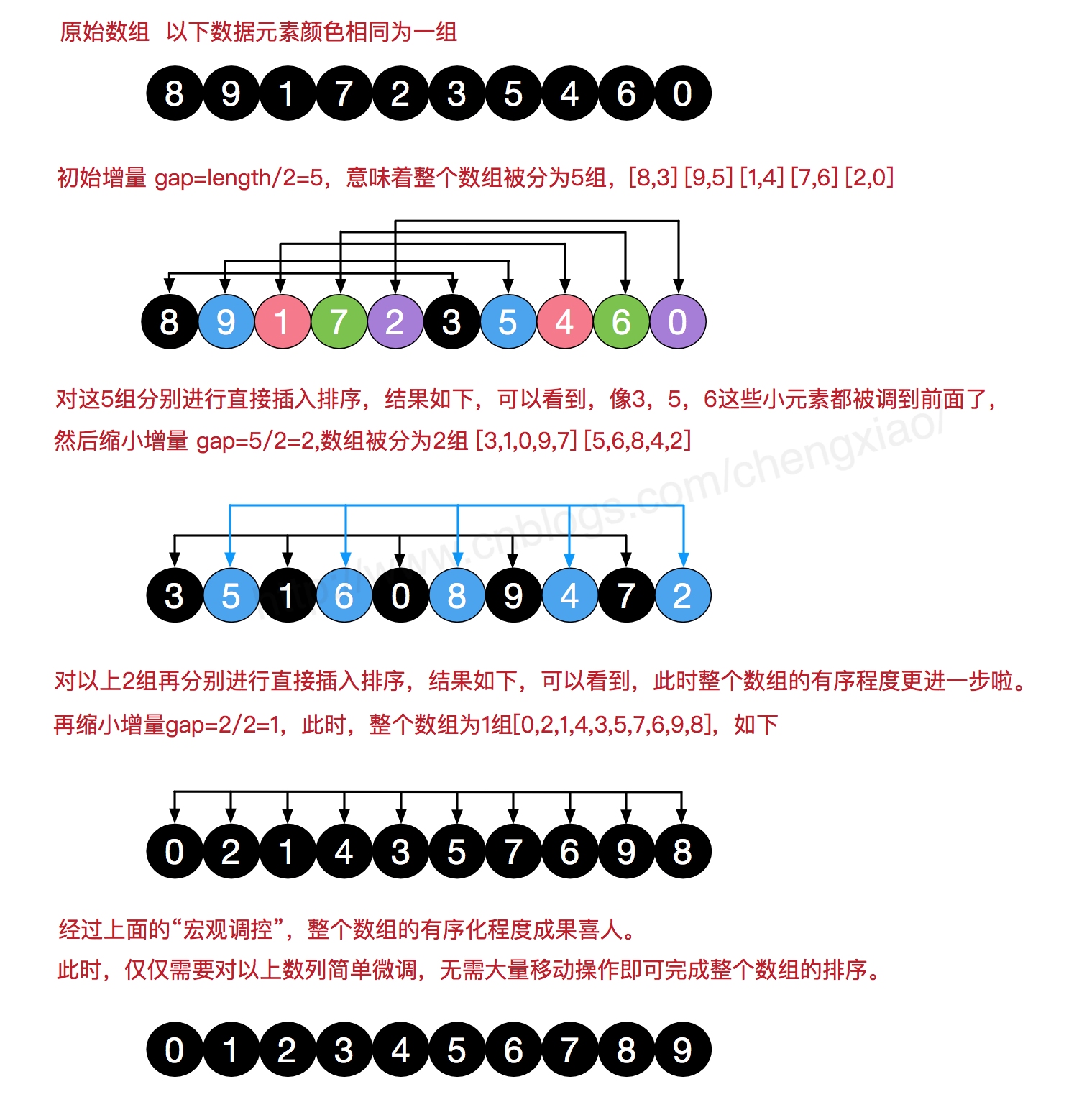
✈️代码实现（coding）

void shellsort(int arr[],int sz){for(int gap = sz/2;gap > 0;gap /= 2){for(int i = gap;i < n;++i){//i从每组的第二个数遍历，因为每组的第一个数不用进行插入排序int k = arr[i];//记录当前进行插入排序的数据for(int j = i;j >= gap && k < arr[j - gap];j -= gap)//如果待插入的数据比前一个数据小就将前一个数移到待排序的位置，接着与下一个位置比较arr[j] = arr[j-gap];arr[j] = k;//最后将要插入的数据插到合适的位置}}
}

希尔排序没有稳定性，是阿辉介绍的第一个时间复杂度突破O(n²)的排序，时间复杂度在O(nlogn)~O(n²)之间，有同学可能会问为啥仅仅分了各组就让希尔排序更快了，问的好重点来了

✈️为啥希尔排序能比插入排序更快

其实一个列子就能让你明白，比如下列这个数组：

对于最后的1插入排序需要交换5次才能来到正确的位置
而如果使用希尔排序，对于第一个增量3，1将与8一组，一次交换就让1跨过了3和4下标的位置，从而少了2次交换，所以希尔排序比插入排序更快，它降低了交换的次数

---

其实，阿辉介绍的这些比较挫的排序，之所以挫就是因为它们大量浪费了交换，后续阿辉介绍的时间复杂度在O(nlogn)的排序都减少了交换的次数