在acwing学习算法的一点思考和总结

---

 状态压缩dp可以用来解决两种问题：一种是棋盘式的，也就是表示一行有2^N种摆法，另一种是表示一类集合

状压——棋盘式

 思路：可以类比一下蒙德里安的梦想的解题过程，每一行的状态都只会受到上一层状态的影响。那么我们在更新第i行的状态时，我们枚举一下第i - 1行的状态。也就是当这两行的对应状态是个合法状态的话，我们就进行方案数的累加。

确定状态转移方程：f[i][a] += f[i-1][b]，表示前i行，并且第i行是第j种摆法 的最大种植方案数

预处理：为了判断哪两种行状态是对应合法的，我们需要进行预处理，找出相邻两行能进行转移的状态（二进制表达）。具体题目具体分析，在这个题目中，第一要满足左右相邻不能都是1，第二要满足上下相邻不能都是1

/*
前i行，并且第i行是第j种摆法 的最大种植方法
*/
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>using namespace std;
const int N = 14, M = 1<<12, mod = 1e8;
vector<int> head[M]; //存储合法的转移状态
vector<int> state;
int f[N][M];
int n,m;
int g[N];bool check(int x)
{for(int i = 0; i < m; i ++){if(( (x >> i) & 1) && (x>> (i+1) & 1) )return false;}return true;
}int main()
{cin>>n>>m;for(int i = 1; i <= n; i ++)for(int j = 0; j < m; j ++){int t;cin>>t;g[i] += !t * (1 << j);            }for(int i = 0; i < 1<<m; i ++ ){if(check(i)){state.push_back(i); //初次筛选：左右相邻不能同时为1}}for(int i = 0; i < state.size(); i ++){for(int j = 0; j < state.size(); j ++){int a = state[i], b = state[j];if( (a & b) == 0) //上下相邻不能同时为1{head[i].push_back(j); //若是合法就加入到可转移数组中}}}f[0][0] = 1;for(int i = 1; i <= n + 1; i ++){for(int a = 0; a < state.size(); a ++){if(!(state[a] & g[i]))for(int b : head[a])f[i][a] =(f[i][a] + f[i-1][b]) % mod;}}cout<<f[n+1][0];}

状压——集合

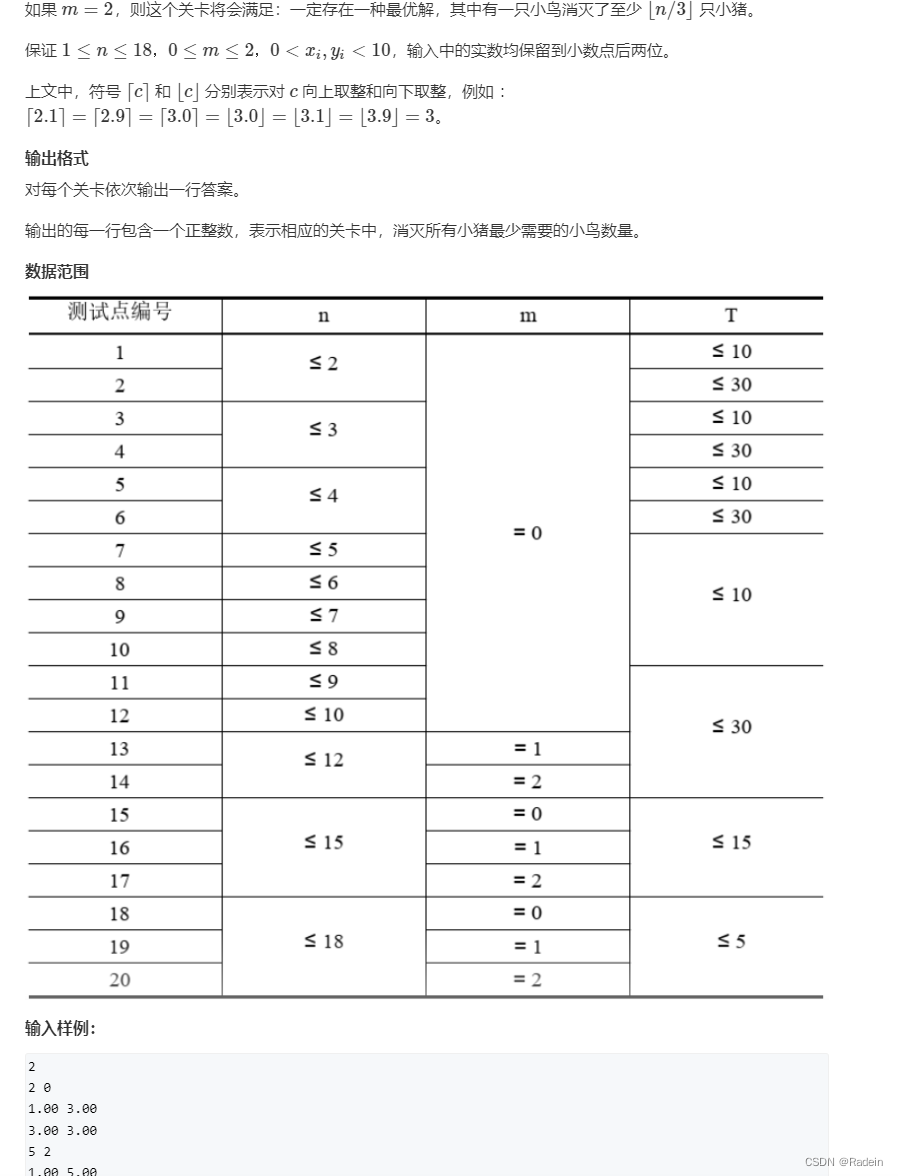
所有小猪击中状态由一串二进制数来表达，若一个小猪能被击中，那么该小猪对应到二进制表达上的位置就制成1。那么我们接下来要做的就是枚举所有抛物线，并求一下抛物线能击中哪些小猪。并将这个结果存放在path数组里。

state: 二进制表达式，如1100，表示前两只小猪没被击中，后两只被击中了

path[i][j] = state : 含义：经过点i和j的抛物线； 属性：遗传二进制数，表示所有小猪的状态

f[i]: i其实就是state，从0~2^N枚举i的二进制表达，直到枚举到111111（所有位上都是1时）说明所有小猪均已经被击落。 那么f[i]的含义就是所有小猪在该状态下最少可以用多少条抛物线覆盖

那么接下来就是枚举所有状态下的小猪的覆盖方式，更新最小覆盖的抛物线数量

#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
#include<cmath>#define x first
#define y secondusing namespace std;
typedef pair<double, double> PDD;
const int N = 18, M = 1<<18;
const double eps = 1e-8;
int f[M];
PDD q[N];
int path[N][N];
int n,m;int cmp(double x, double y)
{if(fabs(x - y) < eps) return 0;if(x < y) return -1;return 1;
}int main()
{int T;cin>>T;while(T--){cin>>n>>m;for(int i = 0; i<n; i ++) cin>>q[i].x>>q[i].y;memset(path, 0, sizeof path);for(int i = 0; i < n; i ++)  //枚举所有的二次函数方程（两点确定一个抛物线，因为抛物线过原点），这里是找第一个点{path[i][i] = 1 << i;for(int j = i; j < n; j ++) //找这个函数的第二个点{double x1 = q[i].x, x2 = q[j].x;double y1 = q[i].y, y2 = q[j].y;if(!cmp(x1,x2)) continue;double a = (y1 / x1 - y2 / x2) / (x1 - x2); //通过两点，解出抛物线方程double b = y1 / x1 - a * x1;if(cmp(a, 0) >= 0) continue;int state = 0;for(int k = 0; k < n; k ++) //计算有多少点在这条抛物线上{   double x = q[k].x, y = q[k].y;if(!cmp(a*x*x + b * x, y)) state +=1 << k;}path[i][j] = state;}}memset(f, 0x3f, sizeof f);f[0] = 0;                          for(int i = 0; i < 1<<n; i ++) //枚举所有小猪击中状态{int x = 0;for(int j = 0; j < n; j ++) //若找到没被击中的小猪，那就要更新f[i]。{if(!( i >> j & 1)){x = j;break; //注意到这里是break，即只用更新一次，因为后面还会进行一次更新，避免掉重复的更新工作}}for(int k = 0; k < n; k ++){f[i | path[x][k]] = min(f[i | path[x][k]], f[i] + 1);}}cout<<f[(1<<n) - 1]<<endl;}
}