文中程序以Tensorflow-2.6.0为例
部分概念包含笔者个人理解,如有遗漏或错误,欢迎评论或私信指正。
截图和程序部分引用自北京大学机器学习公开课
TF2基础常用函数
1、张量处理类
强制数据类型转换:
a1 = tf.constant([1,2,3], dtype=tf.float64)
print(a1)
a2 = tf.cast(a1, tf.int64) # 强制数据类型转换
print(a2)
查找数据中的最小值和最大值:
print(tf.reduce_min(a2), tf.reduce_max(a2))
上一行例子中是对整个张量查找,也按照一定的方向查找,只按照行或只按照列,这由axis变量决定。通常axis=0代表按列查找,axis=1代表按行查找
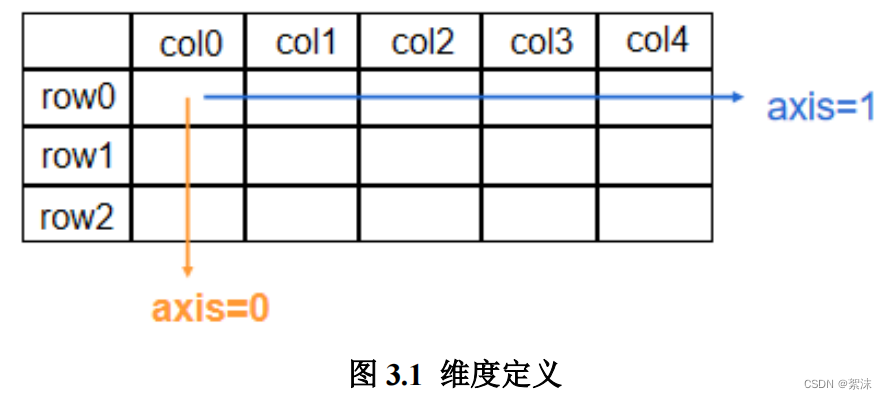
a1 = tf.constant([[1,2,3],[2,3,4]])
print(a1)
print(tf.reduce_max(a1, axis=0)) # 按照列查找最大的行
print(tf.reduce_sum(a1,axis=1)) # 按照行计算各列的和
常见的张量检索类函数在tf.reduce_xxx可以查看
张量中数据的索引,可以按照行,或者按照列索引一个张量数据中的最大值和最小值
test = np.array([[1, 2, 3],[2, 3, 4],[5, 6, 7], [7, 8, 2]])
print(test)
print(tf.argmax(test, axis=0)) # 按列查找,找到每一列的最大值序列号
print(tf.argmax(test, axis=1)) # 按行查找,找到每一行的最大值序列号
2、数学运算类
四则运算类:(注意:只有维度相同的数据才可以做四则运算,运算均是对应位置元素进行计算,同时tf中,除非指定,默认生成的张量数据时类型为int32或float32)
a1 = tf.constant([[1,2,3],[1,2,3]])
a2 = tf.constant([[2,3,4],[2,3,4]])
print(tf.add(a1, a2)) # 加
print(tf.subtract(a1, a2)) # 减
print(tf.multiply(a1, a2)) # 乘
print(tf.divide(a1, a1)) # 除
平方与开根号:(这里的计算同样是对应位置元素进行计算)
a1 = tf.fill([1,3], 3.) # 这里的指定值为3. 小数点是为了生成float32类型数据
print(a1)
print(tf.pow(a1, 3)) # 开三次方根,第二个参数就是开根的次数
print(tf.square(a1)) # 平方
print(tf.square(a1)) # 开方
张量的叉乘(向量积):
a = tf.ones([3, 2]) # 3行2列
b = tf.fill([2, 3], 3.) # 2行3列
print(tf.matmul(a, b)) # 矩阵叉乘得6行6列,叉乘的两个矩阵,前者的列数必须和后者的行数相等
3、训练处理类
标记训练参数,网络训练的过程实质上最重要的就是更新网络中的参数,所以需要告知网络中哪一个参数是可以被跟新的,这样tensorflow框架会自动的在网络反向传播的过程中记录每一层的梯度信息,便于处理。
# tf.Variable(初始值) 函数用于标记可变参数
tf.Variable(tf.random.normal([2,2],mean=0,stddev=1))
标签/特征数据处理,训练之前,预先准备的特征数据和标签数据往往是区分开的,所以需要将他们一 一对应上。将输入数据的特征和标签对应匹配,构建出新的用于训练的变量:
# data = tf.data.Dataset.from_tensor_slices((特征数据, 标签数据)) 可以直接输入numpy或者tensor格式的数据
features = tf.constant([12, 15, 20, 11]) # 特征数据
labels = tf.constant([0, 1, 1, 0]) # 标签
dataset = tf.data.Dataset.from_tensor_slices((features, labels)) # 对应结合
for element in dataset:print(element) # 输出
在上面的程序中from_tensor_slices()函数要求两个数据的第一个维度的大小必须相同即可,所以第一行的特征数据也可以改为:
features = tf.constant([[12,13], [15,16], [20,21], [10,11]]) # 第一个维度任然是4
记录梯度,以及自动微分,在训练的过程中自动跟新参数是一个循环加反向传播的过程,反向传播时,我们需要知道每个网络层中损失函数的梯度,在tf中可以使用上下文记录器自动在迭代过程中记录每个层的梯度信息。这主要由两个函数组成tf.GradientTape() 函数起到上下文记录的作用,用于记录层信息,gradient()函数用于求导即求梯度
with tf.GradientTape() as tape: # 记录下两行的层信息w = tf.Variable(tf.constant(3.0)) # 标记可变参数loss = tf.pow(w, 2) # 设置损失函数类型
grad = tape.gradient(loss, w) # 损失函数对w求导
print(grad)
在上面的代码中tf.pow(w, 2)表示损失函数为 l o s s = w 2 loss = w^2 loss=w2 梯度求导后得到 ∂ w 2 ∂ w = 2 w \frac{\partial w^2}{\partial w} = 2w ∂w∂w2=2w 由于初始的参数w为3.0,求导后结果为6.0,程序结果grad为6。注意此处使用的with as结构中必须申明被导的变量,这样才能正常生效记录数据。
枚举数据,为了遍历数据并逐个处理,使用python中内置的enumerate(列表名)进行数据的枚举,通常配合for使用。
# 枚举列表
data = ['one', 'two', 'three']
for i, element in enumerate(data): # 返回的第一个是序列号,第二个是内容print(i, element)
独热编码,在分类的问题中我们还需要了解独热码的概念,通常使用独热码作为标签数据,在被标记的类别中1表示是,0表示非,可以通俗理解为:有几类被分类数据独热码就有几个,每一类数据对应一个的独热码,类似译码器选址原理。
举例,有3个类
那么第一类的独热码是: 1 0 0
第2类的独热码是: 0 1 0
第3类的独热码是: 0 0 1
在tf中转化独热码:
classes = 4 # 标签数
labels = tf.constant([1, 0, 6 ,3]) # 输入标签数据
output = tf.one_hot(labels, depth=classes) # 独热码转换,第一个变量为输入的标签数据,第二个为类别数
print(output)
上面使用了tf.one_hot()函数用来转化独热码,值得注意的是输入的数据会自动的从小到大排序后再转化对应的独热码。所以上面的程序输出了
tf.Tensor(
[[0. 1. 0. 0.] # 对应1[1. 0. 0. 0.] # 对应0[0. 0. 0. 0.] # 对应6[0. 0. 0. 1.]], # 对应3shape=(4, 4), dtype=float32)
softmax()函数,在网络输出的结果中,如果直接按照最终输出的值判断类型结果往往比较抽象。比如网络最终会输出一个矩阵[2.52, -3.1, 5.62],那么如何确定这个矩阵是对应哪一个类别。这里我们需要通过归一化和概率来判断,假设这个输出的三列矩阵分别对应三个类别的得分数值,那我们可以将三个值相加求和再分别除以各自来得到每个数的百分比占比。当然在机器学习中softmax()也是类似这样做的,不过为了避免负数和特殊0值以及数据的连续性,引入指数函数辅助计算:
S o f t m a x ( y i ) = e y i ∑ j = 0 n e y i \mathit{Softmax(y_{i} )=\frac{e^{y_{i} } }{ {\textstyle \sum_{j=0}^{n}e^{y_{i} {\LARGE {\ } } } } } } Softmax(yi)=∑j=0neyi eyi 同时softmax()函数的输出符合概率分布定义: ∀ x , P ( X = x ) ∈ [ 0 , 1 ] 且 ∑ x P ( X = x ) = 1 \mathit{{\LARGE } \forall x, P(X=x)\in [0, 1] 且\sum_{x}^{} P(X=x)=1 } ∀x,P(X=x)∈[0,1]且x∑P(X=x)=1 所以在上面的[2.52, -3.1, 5.62]例子中不难计算得到对应结果为[0.256, 0.695, 0.048]
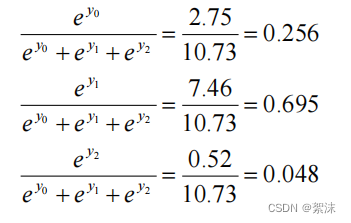
第二列最大,所以我们可以认为这个输出举证表示第二类的可能性最大。综上softmax()的属性决定它大多数时候应用在网络的输出位置。
y = tf.constant([1.01, 2.02, -1.11])
y_out = tf.nn.softmax(y)
print("data {}, after softmax is {}".format(y, y_out))
跟新权重参数,在上面的程序中完成了数据的读入,损失梯度计算那么计算过的结果就需要计时更新到权重上。值得注意,跟新参数之前一定要申明参数是可训练自更新的。通常计算得到梯度后直接跟新参数就可以完成一次反向传播。
w = tf.Variable(4) # 申明可变参数,并赋初值为4
w.assign_sub(1) # 对可变参数执行一次自减跟新,传入参数为被减数
print(w)
根据鸢尾花数据进行简单的分类任务
软件环境:
cuda = 11.2
python=3.7
numpy==1.19.5
matplotlib== 3.5.3
notebook==6.4.12
scikit-learn==1.2.0
tensorflow==2.6.0
分类时主要有以下几步:
1、加载数据:
# 导入所需模块
import tensorflow as tf
from sklearn import datasets
from matplotlib import pyplot as plt
import numpy as np
# 导入数据,分别为输入特征和标签
x_data = datasets.load_iris().data
y_data = datasets.load_iris().target
2、打乱数据顺序(由于这里的数据是直接加载已有数据,所以先打乱,对于其他数据不一定要这步),分割数据为训练部分和测试部分:
# 随机打乱数据(因为原始数据是顺序的,顺序不打乱会影响准确率)
# seed: 随机数种子,是一个整数,当设置之后,每次生成的随机数都一样
np.random.seed(116) # 使用相同的seed,保证输入特征和标签一一对应
np.random.shuffle(x_data)
np.random.seed(116)
np.random.shuffle(y_data)
tf.random.set_seed(116)
# 将打乱后的数据集分割为训练集和测试集,训练集为前120行,测试集为后30行
x_train = x_data[:-30]
y_train = y_data[:-30]
x_test = x_data[-30:]
y_test = y_data[-30:]
3、转换数据类型格式,匹配特征数据和标签数据,设置训练可变参数
# 转换x的数据类型,否则后面矩阵相乘时会因数据类型不一致报错
x_train = tf.cast(x_train, tf.float32)
x_test = tf.cast(x_test, tf.float32)# from_tensor_slices函数使输入特征和标签值一一对应。(把数据集分批次,每个批次batch组数据)
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)# 生成神经网络的参数,4个输入特征故,输入层为4个输入节点;因为3分类,故输出层为3个神经元
# 用tf.Variable()标记参数可训练
# 使用seed使每次生成的随机数相同(方便教学,使大家结果都一致,在现实使用时不写seed)
w1 = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1, seed=1))
b1 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1))
4、初始化超参数
lr = 0.1 # 学习率为0.1
train_loss_results = [] # 将每轮的loss记录在此列表中,为后续画loss曲线提供数据
test_acc = [] # 将每轮的acc记录在此列表中,为后续画acc曲线提供数据
epoch = 500 # 循环500轮
loss_all = 0 # 每轮分4个step,loss_all记录四个step生成的4个loss的和
5、开始训练
# 训练部分
for epoch in range(epoch): #数据集级别的循环,每个epoch循环一次数据集for step, (x_train, y_train) in enumerate(train_db): #batch级别的循环 ,每个step循环一个batchwith tf.GradientTape() as tape: # with结构记录梯度信息y = tf.matmul(x_train, w1) + b1 # 神经网络乘加运算y = tf.nn.softmax(y) # 使输出y符合概率分布(此操作后与独热码同量级,可相减求loss)y_ = tf.one_hot(y_train, depth=3) # 将标签值转换为独热码格式,方便计算loss和accuracyloss = tf.reduce_mean(tf.square(y_ - y)) # 采用均方误差损失函数mse = mean(sum(y-out)^2)loss_all += loss.numpy() # 将每个step计算出的loss累加,为后续求loss平均值提供数据,这样计算的loss更准确# 计算loss对各个参数的梯度grads = tape.gradient(loss, [w1, b1])# 实现梯度更新 w1 = w1 - lr * w1_grad b = b - lr * b_gradw1.assign_sub(lr * grads[0]) # 参数w1自更新b1.assign_sub(lr * grads[1]) # 参数b自更新
6、训练的同时在每个epoch中进行一次测试(实际训练时,若果测试输出需要耗时较高,可以每10次进行一次测试)
# 测试部分# total_correct为预测对的样本个数, total_number为测试的总样本数,将这两个变量都初始化为0total_correct, total_number = 0, 0for x_test, y_test in test_db:# 使用更新后的参数进行预测y = tf.matmul(x_test, w1) + b1y = tf.nn.softmax(y)pred = tf.argmax(y, axis=1) # 返回y中最大值的索引,即预测的分类# 将pred转换为y_test的数据类型pred = tf.cast(pred, dtype=y_test.dtype)# 若分类正确,则correct=1,否则为0,将bool型的结果转换为int型correct = tf.cast(tf.equal(pred, y_test), dtype=tf.int32)# 将每个batch的correct数加起来correct = tf.reduce_sum(correct)# 将所有batch中的correct数加起来total_correct += int(correct)# total_number为测试的总样本数,也就是x_test的行数,shape[0]返回变量的行数total_number += x_test.shape[0]# 总的准确率等于total_correct/total_numberacc = total_correct / total_numbertest_acc.append(acc)
7、输出结果,可视化训练过程
# 绘制 loss 曲线
plt.title('Loss Function Curve') # 图片标题
plt.xlabel('Epoch') # x轴变量名称
plt.ylabel('Loss') # y轴变量名称
plt.plot(train_loss_results, label="$Loss$") # 逐点画出trian_loss_results值并连线,连线图标是Loss
plt.legend() # 画出曲线图标
plt.show() # 画出图像# 绘制 Accuracy 曲线
plt.title('Acc Curve') # 图片标题
plt.xlabel('Epoch') # x轴变量名称
plt.ylabel('Acc') # y轴变量名称
plt.plot(test_acc, label="$Accuracy$") # 逐点画出test_acc值并连线,连线图标是Accuracy
plt.legend()
plt.show()