自然数平方倒数求和Σ1/n²是一个并不复杂的问题,但它困扰了欧洲大陆整整90年,在欧系数学里它被称为“巴塞尔级数”。
解决巴塞尔级数让欧拉一战成名,然而欧拉采用的方法对数学这门学问是严重的侮辱。数学是工具学科,数学的宗旨是化繁为简,欧拉则反其道而行,他的方法并非依据数学规则,而是个人的胡作非为;虽然最终他给出了正确答案,但利用的原理、采用的方法对后世影响、对数学发展贻害巨大。
 整理后的欧拉Σ1/n²证明方法
整理后的欧拉Σ1/n²证明方法
欧拉对Σ1/n²的证明方法极其繁杂,他的答案不是出于逻辑推导、而是出于某种猜想,是他事先实算、为了附会π²/6答案而倒逼来的步骤。
 拥趸对欧拉证明Σ1/n²予以无限溢美和附会
拥趸对欧拉证明Σ1/n²予以无限溢美和附会
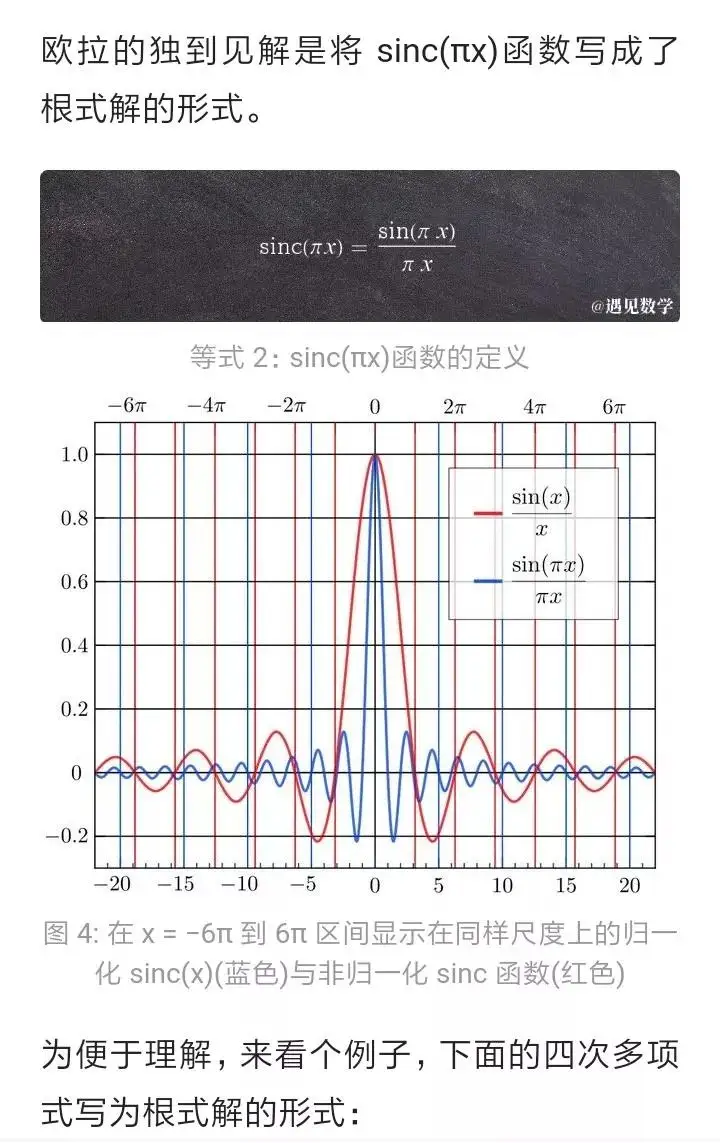 sinc、sin、πx及无厘头等式被认为是独到见解
sinc、sin、πx及无厘头等式被认为是独到见解
 欧拉关于巴塞尔级数的证明概述
欧拉关于巴塞尔级数的证明概述
多达10个突兀而来的“演变等式”,全是欧拉一个人的随心所欲,他看似玄妙的思维,其实不过都是“预设”而来的无事生非,以sinc(πx)=sin(πx)/πx而言,它是什么道理、与1/n²有什么关联?我说欧拉就是在自以为是自欺欺人,他不管谁是谁、谁跟谁,分数式、数据量、圆周率π、代数x、三角函数sin全都来得莫名其妙,这事儿如果常人所为必定是学术欺诈,但用于欧拉却是“独到见解”。
欧拉对巴塞尔级数的证明,没有一个人能真正看明白,大家因为自己不懂而不敢去直视,就如同“皇帝的新装”一样生怕被人看扁,欧洲人觉得“π²/6”这个答案太清新脱俗了,就不问过程给予了掌声,问题是270年来就没有人能认真一点、勇敢一点吗?
我不明白为什么欧洲人会对Σ1/n²一筹莫展,在我看来这个问题十分简单。2016年我与一个吧友打赌“微积分能解决的问题,算术法都能解决(他认为Σ1/n²非微积分不能解决)”,仅一周时间我就找到了三种算术方法,其中最简单的一种只需要“三步(第一步辅以中国定理,第二步辅以灭项数列,第三步得出答案)”:1+1/4+1/9+…+1/n²+…=1+(1/4+1/16+…+1/4^k)+(1/9+1/81+…+1/9^k)+(1/25+1/625+…+1/25^k)+…+[1/n²+1/n^4+…+1/n^(2k)]=1+1/3+1/8+1/24+…+1/(n²-1)【注n≠M,M表示灭项数列(n+1)^(k+1)】=1+Σ1/(n²-1)-Σ1/(M²-1)=1+3/4-0.1050659331…=1.6449340668…=π²/6。这种基于数学原理、初通数学就能看懂的解法才是真正的数学!欧拉的拥趸会说“你求的是数值、不能用圆周率π表示”,对此我想提醒他们:比起欧拉的“π如何来历”弄虚作假,1.6449340668…=π²/6是严格的等量计算,须知π只是代码,π=周长/直径=3.1415926535…才是π的本质。
欧拉对巴塞尔级数的装神弄鬼设计严重地误导了数学人在此类问题上的思路,导致了数学界在相关问题上一直在化简为繁、陷在级数、积分坑里走不出来。
 据统计Σ1/n²有23种证明方法
据统计Σ1/n²有23种证明方法
 对Σ1/n²最简单的一种证明方法
对Σ1/n²最简单的一种证明方法
欧拉以后,欧系数学家又整理搜罗了22种Σ1/n²证明方法。这23种方法每一个都艰涩繁琐、都脱离了1/n²本身、都属于画蛇添足,给人的感觉是:北京到天津东去120公里即可,偏偏要绕行成都新加坡迪拜巴黎纽约海参崴沈阳一大圈!难道对1+1/4+1/9+…+1/n²+…直接使用加减乘除,不比用傅里叶级数、微分积分更简便吗?
纯粹数学现在之所以步入了死胡同,是因为它为了形式冥顽不化、为达目的不择手段;现代数学越来越艰难、越来越花哨,是由于纯粹数学在反客为主,而纯粹数学因为欧拉的上梁不正脱离实践、难度系数至少增加了10倍以上。