🌈个人主页:秦jh__https://blog.csdn.net/qinjh_?spm=1010.2135.3001.5343
🔥 系列专栏:《数据结构》https://blog.csdn.net/qinjh_/category_12536791.html?spm=1001.2014.3001.5482

目录
二叉树遍历规则
前序遍历
中序遍历
后序遍历
递归结构遍历
前序
中序
求节点个数
求叶子节点个数
求树的高度
求第k层节点个数
前言
💬 hello! 各位铁子们大家好哇。
今日更新了树的遍历,递归的相关内容
🎉 欢迎大家关注🔍点赞👍收藏⭐️留言📝
二叉树遍历规则

前序遍历
注意:N代表空
分析:根据前序遍历的规则(根左右),先访问根1,然后左子树2,2的左子树3,3的左子树是N,右子树也是N,然后返回到2的右子树N,然后返回到1的右子树4,接着是4的左子树5,5的左右子树都是N,然后返回到4的右子树6,6的左右子树都是N。
中序遍历
分析:根据规则(左根右),1的左子树2,2的左子树3,3的左子树N,起始即为N,接着是根3,接着是3的右子树N,返回到根2,然后是2的右子树N,返回到根1,接着是1的右子树,以此类推。
后序遍历
分析:过程变为左右根,其实质与前面两种一样。
递归结构遍历

上图是要遍历的树的模型。
前序
假设树已构建好,下图是前序遍历的函数,执行后即可得到前序遍历的结果。

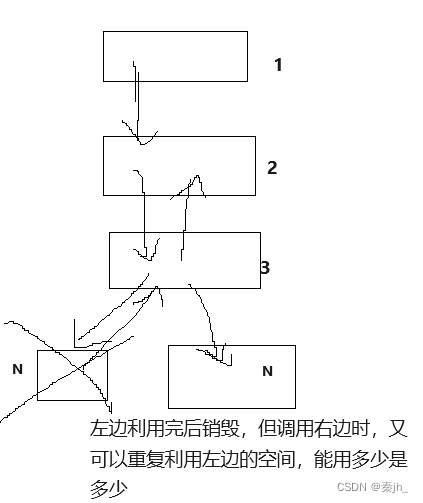
下图是递归的流程图:
分析:开始先打印根1,然后递归调用根2,以此类推到3的左子树N。此时左子树遍历完,返回到3的右子树,每次调用完就返回到上一层的函数中。
上图是递归调用占用的大致空间,每次调用完函数,返回到上一层,上一层接着调用,就会重复利用之前销毁的空间,如果空间不足,能用多少是多少。因此,递归的空间复杂度是看递归的深度。
中序

上图是中序遍历的函数,递归过程参考前序遍历过程。
后序遍历大致过程也同上,这里就不再写出。
求节点个数

递归过程图如下:

分析:如果根结点为空,则返回0。此递归过程会先找出左子树的节点个数,当遇到空节点时就返回0,然后加上根结点自身数量1,返回到上一层,以此类推。
求叶子节点个数
 参考前面的递归过程理解。
参考前面的递归过程理解。
求树的高度

求第k层节点个数
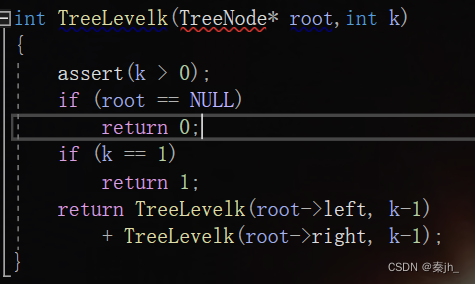
分析:k-1目的是当到达第k层后,直接返回1到上一层
我的博客即将同步至腾讯云开发者社区,邀请大家一同入驻:https://cloud.tencent.com/developer/support-plan?invite_code=3cd3jqfe6fwg0





![[Python] 如何通过ctypes库来调用C++ 动态库 DLL?](https://img-blog.csdnimg.cn/direct/b81cb698689c4fc98e15de89afdd3b24.png)