📚博客主页:爱敲代码的小杨.
✨专栏:《Java SE语法》
❤️感谢大家点赞👍🏻收藏⭐评论✍🏻,您的三连就是我持续更新的动力❤️
🙏小杨水平有限,欢迎各位大佬指点,相互学习进步!

文章目录
- 1. 什么是汉诺塔
- 2. 问题分析
1. 什么是汉诺塔
汉诺塔(Tower of Hanoi),又称河内塔,是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
2. 问题分析
首先我们假设三根柱子为A(起始柱子),B(中转柱子),C(结束柱子);有N个圆盘。
- 当
N = 1时,就只需要移动1次,即A->C

-
当
N = 2时,就需要移动是3次:即A->B、A->C、B->C
-
当
N = 3,就需要移动7次,A->C、A->B、C->B、A->C、B->A、B->C、A->C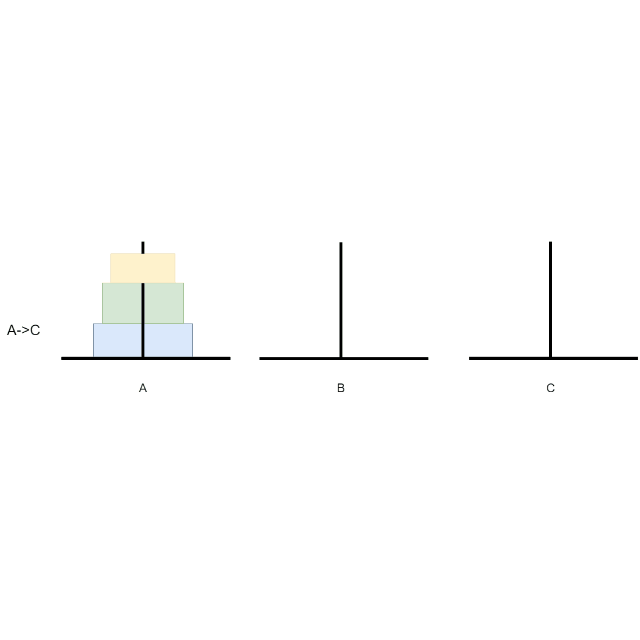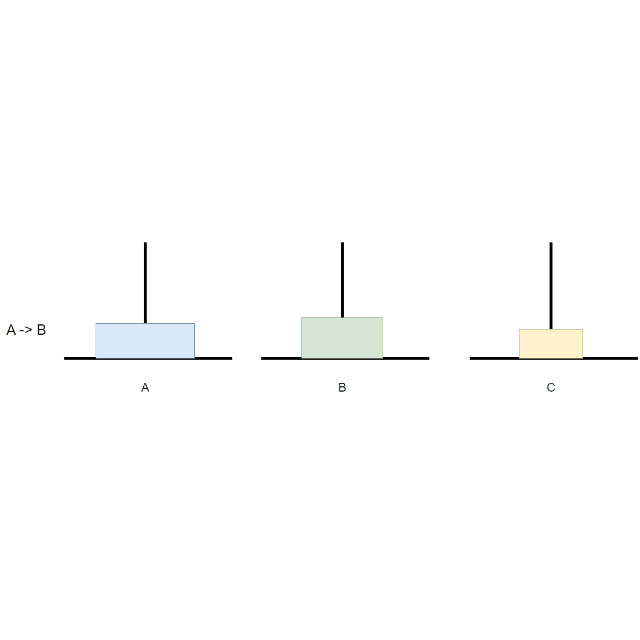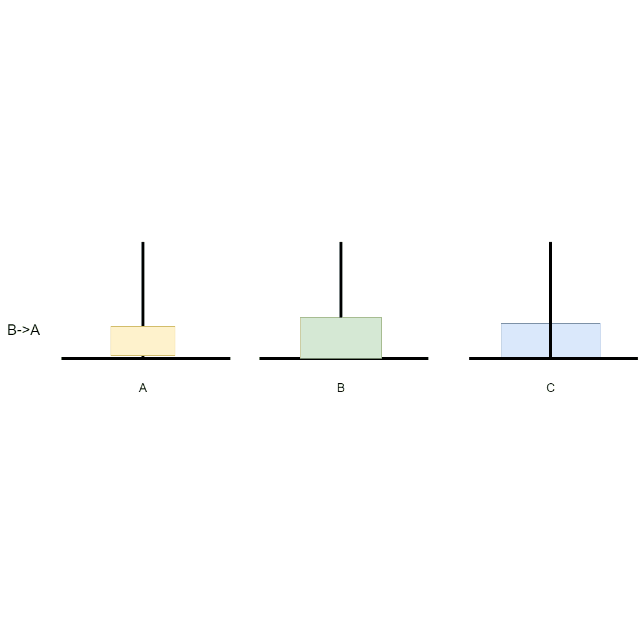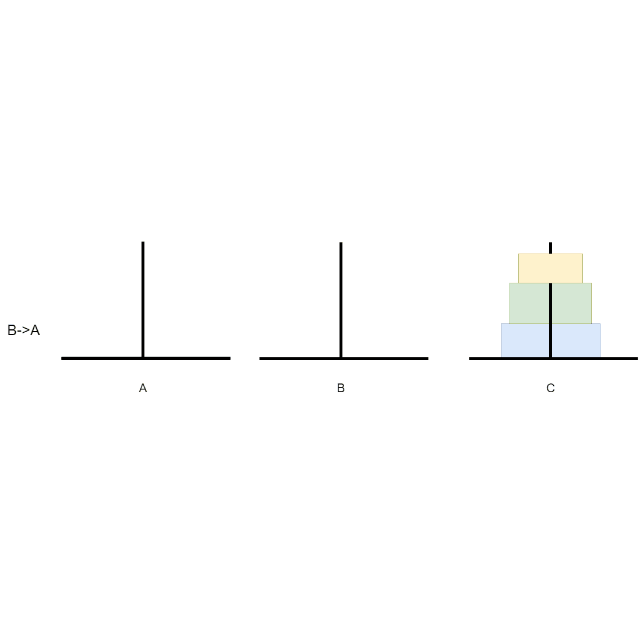
以此类推:移动次数 = 2 ^ 圆盘个数 - 1
所以若有64个圆盘那将会移动 2 ^ 64 - 1次(即:18,446,744,073,709,551,615次),若每次移动需要1s时间,则需要将近5849亿年的时间才能够做到。可见大梵天有多恨婆罗门,这绝对是在坑人啊!!
综上我们可以将问题分解为以下三个步骤:
- 将A柱上的
n-1个盘子移动到B柱上 - 将A柱上剩下的一个盘子移动到C柱上。
- 将B柱上的
n-1个盘子移动到C柱上。
通过递归地执行这三个步骤,我们最终可以实现将所有盘子从A柱移动到C柱的目标。
【注意事项】
- 递归的终止条件:当只有一个盘子时,可以直接将其从A柱移动到C柱,此时递归终止。
- 递归的分解:将问题分解为三个步骤,每次递归调用都是为了完成这三个步骤中的一个。
- 递归的回溯:在完成一个递归调用后,需要将问题状态恢复到递归调用前的状态,以便进行下一个递归调用。
- 递归的效率:汉诺塔问题的递归解法时间复杂度为O(2^n),其中n表示盘子的数量。因此,当盘子数量较大时,递归解法的时间复杂度会非常高。
动画演示:

代码:
public class Test6 {public static void main(String[] args) {hanoi(3, 'A', 'B','C');}/*** 将盘子从pos1移动到pos2* @param pos1 起始柱子* @param pos2 结束柱子*/public static void move(char pos1, char pos2){System.out.print(pos1 + "->" + pos2 + " ");}/**** @param n 盘子个数* @param pos1 起始柱子* @param pos2 中转柱子* @param pos3 目标柱子*/public static void hanoi(int n, char pos1, char pos2, char pos3){if (n == 1){move(pos1, pos3);return;} else{hanoi(n-1, pos1, pos3, pos2);move(pos1, pos3);hanoi(n-1, pos2, pos1, pos3);}}
}
运行结果: