【特征工程】分类变量：简洁而高效的频数编码（Frequency Encoding）-编程知识

【特征工程】分类变量：简洁而高效的频数编码（Frequency Encoding）

频数编码（Frequency Encoding）：一个简洁而高效的特征编码方法

1. 频数编码是什么？

频数编码的主要思想是用每个类别在数据集中出现的频率来替代原始的类别标签。这样可以用一个单一的数值来代表每个类别，而不引入高维度或额外的关系。

这里引入一个数学概念——基数（Cardinality）

基数，即集合中不同元素的数量，也可以用于描述关系数据库中表中列的唯一值的数量。
比如现在有A、B两个集合，其中：

集合 A：[ A = {1, 2, 3, 4, 5, 6, 7} ]
集合 B：[ B = {2, 4, 6, 8, 10} ]

所以，集合 A 的基数是 7，而集合 B 的基数是 5。

**频数编码通常适用于具有高基数（Cardinality）的分类特征。**高基数表示该特征有大量不同的类别或水平。对于低基数的分类特征，意味着元素或值的种类相对较，通常使用独热编码等方法更为合适。

以下是适合使用频数编码的一些情况：

城市/地区名称： 如果你有一个表示城市或地区的分类特征，并且有大量不同的城市或地区，那么使用频数编码可能是一个合理的选择。
用户ID或产品ID： 对于表示用户或产品的唯一标识符的分类特征，如果类别数量很大，频数编码可能会比独热编码更有效。
标签或类别型变量： 当你处理具有大量不同标签或类别的变量时，例如商品类别、文章标签等，频数编码也可以考虑使用。
自然语言处理中的词汇： 在文本数据中，如果你将文本中的词汇转换为分类特征，并且词汇量很大，频数编码可能是一个有用的工具。

2. 优缺点

优点：

简单直观： 频数编码是一种简单而直观的方法，不引入复杂的转换规则，易于理解和实现。
适用于树状模型： 频数编码特别适用于树状模型，如决策树、随机森林和梯度提升树等，因为这些模型能够有效地处理数值型特征。

缺点：

忽略类别之间的内在关系： 频数编码并不考虑类别之间的内在关系，可能无法捕捉潜在的信息。
对于线性模型效果有限： 在处理线性模型时，频数编码可能效果较差，因为线性模型通常更适用于数值型变量。

3. 参考代码案例

以下是使用Python进行频数编码的简单示例：

import pandas as pd# 创建示例数据
data = {'Category': ['A', 'B', 'A', 'B', 'A', 'A', 'B', 'A']}
df = pd.DataFrame(data)# 计算每个类别的频数
frequency_map = df['Category'].value_counts(normalize=True).to_dict()
#frequency_map = df.groupby('Category').size()/len(df)# 将频数编码应用到数据集
df['Category_Frequency'] = df['Category'].map(frequency_map)# 打印编码后的数据
print(df[['Category', 'Category_Frequency']])

输出结果：
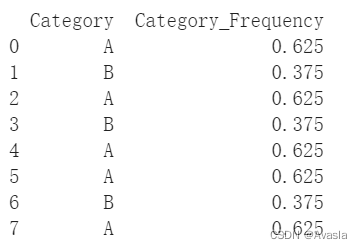
在这里插入图片描述

计算代码解释

代码：df['Category'].value_counts(normalize=True).to_dict()
这行代码的最终目的是返回一个字典，其中包含了’Category’列中每个唯一值的相对频率。下面是代码的解释：

df['Category']: 选择DataFrame中名为’Category’的列，返回一个Series对象，其中包含了该列的所有数值。
.value_counts(): 对该列中的每个唯一值进行计数，返回一个包含唯一值及其对应计数的Series。这个Series按计数值从高到低排序。
normalize=True: 在进行计数时，将计数值除以总数，得到每个唯一值的相对频率（归一化），而不是绝对计数。这样可以得到每个唯一值在列中的比例。
.to_dict(): 将上一步得到的Series转换为一个字典，其中唯一值是字典的键，相对频率是字典的值。

代码： df.groupby('Category').size()/len(df)
这行代码的目的是计算每个’Category’值在整个数据集中的相对频率。结果是一个Series，其中索引是’Category’的唯一值，而值是每个唯一值的相对频率。下面是代码的解释：

df.groupby('Category'): 根据’Category’列的唯一值进行分组，返回一个GroupBy对象。这意味着数据根据’Category’列中的不同值被划分成多个组。
.size(): 对每个分组计算其大小，即每个’Category’值出现的次数。
/len(df): 将每个分组的大小除以整个DataFrame的长度，即总行数。这一步得到的是每个分组的相对频率，因为它是该分组大小占整个数据集大小的比例。