- 一、方差与标准差
- 二、协方差
- 三、皮尔逊系数
- 四、斯皮尔曼系数
- 五、卡方检验
- 六、四分位法和箱线图
- 七、
一、方差与标准差
总体方差
V a r ( x ) = σ 2 = ∑ i = 1 n ( x i − x ˉ ) 2 n = ∑ i = 1 n x i 2 − n x ˉ 2 n = E ( x 2 ) − [ E ( x ) ] 2 Var(x)=\sigma^2=\frac {\sum\limits_{i=1}^{n} (x_i - \bar{x})^2} {n} =\frac{\sum\limits_{i=1}^nx_i^2-n\bar{x}^2} {n} =E(x^2)-[E(x)]^2 Var(x)=σ2=ni=1∑n(xi−xˉ)2=ni=1∑nxi2−nxˉ2=E(x2)−[E(x)]2
样本方差
V a r ( x ) = s 2 = ∑ i = 1 n ( x i − x ˉ ) 2 n − 1 = ∑ i = 1 n x i 2 − n x ˉ 2 n − 1 Var(x)=s^2=\frac {\sum\limits_{i=1}^{n} (x_i - \bar{x})^2} {n-1} =\frac{\sum\limits_{i=1}^nx_i^2-n\bar{x}^2} {n-1} Var(x)=s2=n−1i=1∑n(xi−xˉ)2=n−1i=1∑nxi2−nxˉ2
标准差
S D ( x ) = σ ∣ s = V a r ( x ) SD(x)=\sigma|s=\sqrt{Var(x)} SD(x)=σ∣s=Var(x)
方差用来衡量随机变量离其期望值的分散程度,标准差在方差的基础上消除了量纲的影响。
二、协方差
总体协方差
C o v ( x , y ) = ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) n = ∑ i = 1 n x i y i − n x ˉ y ˉ n {Cov}(x, y) = \frac {\sum\limits_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})} {n} =\frac{\sum\limits_{i=1}^nx_iy_i-n\bar{x}\bar{y}} {n} Cov(x,y)=ni=1∑n(xi−xˉ)(yi−yˉ)=ni=1∑nxiyi−nxˉyˉ
样本协方差
C o v ( x , y ) = ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) n − 1 = ∑ i = 1 n x i y i − n x ˉ y ˉ n − 1 {Cov}(x, y) = \frac {\sum\limits_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})} {n-1} =\frac{\sum\limits_{i=1}^nx_iy_i-n\bar{x}\bar{y}} {n-1} Cov(x,y)=n−1i=1∑n(xi−xˉ)(yi−yˉ)=n−1i=1∑nxiyi−nxˉyˉ
对协方差公式的直观理解:以 ( x ˉ , y ˉ ) (\bar{x}, \bar{y}) (xˉ,yˉ)为坐标原点,计算各个点到原点构成的矩形面积之和,然后除以n-1。其中一三象限面积为正,二四象限面积为负。
协方差的含义可以从以下几个方面理解:
- 正值和负值: 协方差为正表示两个变量呈正相关关系,即一个变量增大,另一个变量也倾向于增大;协方差为负表示两个变量呈负相关关系,即一个变量增大,另一个变量倾向于减小。
- 绝对值的大小: 协方差的绝对值大小表示变量之间的线性关系的强度。绝对值越大,说明两个变量之间的线性关系越强;绝对值越小,说明关系越弱。
- 零值: 协方差为零表示两个变量之间没有线性关系。但需要注意,协方差为零并不意味着两个变量之间没有其他类型的关系,只是没有线性关系。
- 单位: 协方差的单位是两个变量单位的乘积,即结果受量纲的影响。
直观理解可以参考https://www.youtube.com/watch?v=J9pXAfd_Kmc
三、皮尔逊系数
公式1
r = ∑ ( x i − x ˉ ) ( y i − y ˉ ) ∑ ( x i − x ˉ ) 2 ∑ ( y i − y ˉ ) 2 = C o v ( x , y ) σ x σ y r=\frac {\sum (x_i - \bar{x}) (y_i - \bar{y})} {\sqrt{\sum(x_i - \bar{x})^2 \sum(y_i - \bar{y})^2}} =\frac{Cov(x,y)} {\sigma_x\sigma_y} r=∑(xi−xˉ)2∑(yi−yˉ)2∑(xi−xˉ)(yi−yˉ)=σxσyCov(x,y)
公式2
r = 1 n ∑ i = 1 n x i y i − x ˉ y ˉ σ x σ y r=\frac{\frac1n\sum\limits_{i=1}^nx_iy_i-\bar{x}\bar{y}} {\sigma_x\sigma_y} r=σxσyn1i=1∑nxiyi−xˉyˉ
公式1表明皮尔逊系数其实就是x, y的协方差与x, y各自标准差的乘积之比。皮尔逊系数的值域范围为[-1, 1],不受量纲的影响。
下面分别给出值域的证明和公式1–>公式2的推导。
(1)值域证明:
- 令 x i − x ˉ = a i , y i − y ˉ = b i x_i-\bar{x}=a_i,y_i-\bar{y}=b_i xi−xˉ=ai,yi−yˉ=bi,则公式1= ∑ a i b i ∑ a i 2 ∑ b i 2 \frac{\sum{a_ib_i}} {\sqrt{\sum{a_i}^2\sum{b_i}^2}} ∑ai2∑bi2∑aibi
- 根据柯西不等式的一般形式有: ∑ i = 1 n a i 2 ∑ i = 1 n b i 2 ≥ ( ∑ i = 1 n a i b i ) 2 \sum\limits_{i=1}^{n}a_i^2 \sum\limits_{i=1}^{n}b_i^2\ge(\sum\limits_{i=1}^{n}a_ib_i)^2 i=1∑nai2i=1∑nbi2≥(i=1∑naibi)2
- 由1、2知道原式中的分子 ∑ a i b i \sum{a_ib_i} ∑aibi的绝对值必小于等于分母 ∑ a i 2 ∑ b i 2 \sqrt{\sum{a_i}^2 \sum{b_i}^2} ∑ai2∑bi2,所以对应值域[-1,1]
看到一个关于柯西不等式的证明很有意思,分享下。原地址https://zhuanlan.zhihu.com/p/397034475

(2)公式1–>公式2推导:
r = ∑ ( x i − x ˉ ) ( y i − y ˉ ) ∑ ( x i − x ˉ ) 2 ∑ ( y i − y ˉ ) 2 = ∑ ( x i y i − x ˉ y i − x i y ˉ + x ˉ y ˉ ) ∑ ( x i 2 − 2 x i x ˉ + x ˉ 2 ) ∑ ( y i 2 − 2 y i y ˉ + y ˉ 2 ) = ∑ x i y i − n x ˉ y ˉ − n x ˉ y ˉ + n x ˉ y ˉ ( ∑ x i 2 − 2 n x ˉ 2 + n x ˉ 2 ) ( ∑ y i 2 − 2 n y ˉ 2 + n y ˉ 2 ) = ∑ x i y i − n x ˉ y ˉ ( ∑ x i 2 − n x ˉ 2 ) ( ∑ y i 2 − n y ˉ 2 ) \begin{aligned} r&=\frac {\sum(x_i - \bar{x}) (y_i - \bar{y})} {\sqrt{\sum(x_i - \bar{x})^2 \sum(y_i - \bar{y})^2}}\\ &=\frac{\sum(x_iy_i-\bar{x}y_i-x_i\bar{y}+\bar{x}\bar{y})} {\sqrt{\sum(x_i^2-2x_i\bar{x}+\bar{x}^2) \sum(y_i^2-2y_i\bar{y}+\bar{y}^2)}}\\ &=\frac{\sum{x_iy_i}-n\bar{x}\bar{y}-n\bar{x}\bar{y}+n\bar{x}\bar{y}} {\sqrt{(\sum{x_i^2}-2n\bar{x}^2+n\bar{x}^2) (\sum{y_i^2}-2n\bar{y}^2+n\bar{y}^2)}}\\ &=\frac{\sum{x_iy_i}-n\bar{x}\bar{y}} {\sqrt{(\sum{x_i^2}-n\bar{x}^2) (\sum{y_i^2}-n\bar{y}^2)}} \end{aligned} r=∑(xi−xˉ)2∑(yi−yˉ)2∑(xi−xˉ)(yi−yˉ)=∑(xi2−2xixˉ+xˉ2)∑(yi2−2yiyˉ+yˉ2)∑(xiyi−xˉyi−xiyˉ+xˉyˉ)=(∑xi2−2nxˉ2+nxˉ2)(∑yi2−2nyˉ2+nyˉ2)∑xiyi−nxˉyˉ−nxˉyˉ+nxˉyˉ=(∑xi2−nxˉ2)(∑yi2−nyˉ2)∑xiyi−nxˉyˉ
分子分母除以n,结合上面方差的公式即可证明。
四、斯皮尔曼系数
斯皮尔曼系数的计算和皮尔逊系数相同,唯一区别只是将皮尔逊系数中的原始值替换为了原始值所对应的秩(序号)。
假设有两个 ( x , y ) (x,y) (x,y)的变量,对应的顺序编号为 ( R ( x ) , R ( y ) ) (R(x),R(y)) (R(x),R(y)),将 ( R ( x ) , R ( y ) ) (R(x),R(y)) (R(x),R(y))当做 ( x , y ) (x,y) (x,y)代入到皮尔逊系数公式则得到斯皮尔曼系数的一般计算公式:
ρ = ∑ ( R ( x i ) − R ( x i ) ˉ ) ( R ( y i ) − R ( y i ) ˉ ) ∑ ( R ( x i ) − R ( x i ) ˉ ) 2 ∑ ( R ( y i ) − R ( y i ) ˉ ) 2 = C o v ( R ( x ) , R ( y ) ) σ R ( x ) σ R ( y ) \rho=\frac {\sum (R(x_i) - \bar{R(x_i)}) (R(y_i) - \bar{R(y_i)})} {\sqrt{\sum(R(x_i) - \bar{R(x_i) })^2 \sum(R(y_i) - \bar{R(y_i)})^2}} =\frac{Cov(R(x),R(y))} {\sigma_{R(x)} \sigma_{R(y)}} ρ=∑(R(xi)−R(xi)ˉ)2∑(R(yi)−R(yi)ˉ)2∑(R(xi)−R(xi)ˉ)(R(yi)−R(yi)ˉ)=σR(x)σR(y)Cov(R(x),R(y))
当 x , y x,y x,y中均不包含重复值时,可以使用下面的简单公式计算:
r = 1 − 6 ∑ d i 2 n ( n 2 − 1 ) r=1-\frac{6\sum{d_i^2}} {n(n^2-1)} r=1−n(n2−1)6∑di2
其中 d i = R ( x i ) − R ( y i ) d_i=R(x_i)-R(y_i) di=R(xi)−R(yi),表示 x , y x,y x,y之间的序号差。下面先举个例子了解实际如何计算,再给出一般公式到简单公式的证明。
(1)实际计算
这里直接拿维基百科上的截图,下面的数据中, X , Y X,Y X,Y分别表示智商和每周看电视的时间。
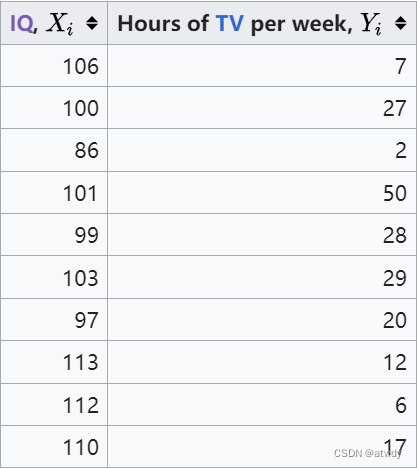
接下来先根据 X i X_i Xi进行排序,得到rank x i x_i xi,再在 X i X_i Xi排完序的基础上,对 Y i Y_i Yi进行排序,得到rank y i y_i yi,然后分别计算它们之间的序号差 d i d_i di和 d i 2 d_i^2 di2。
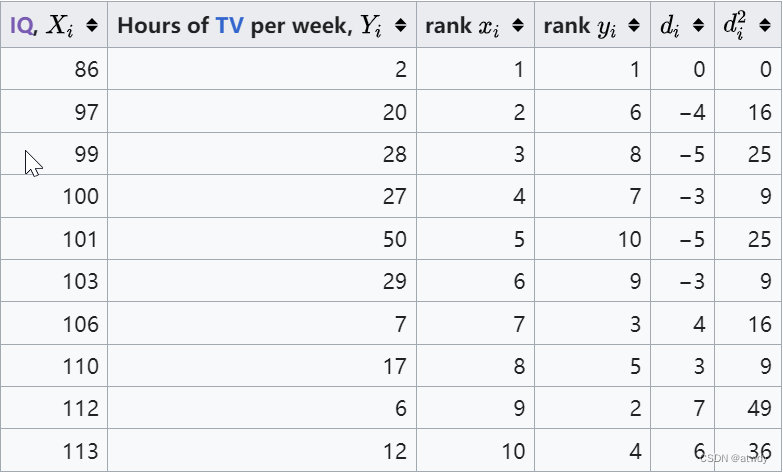
最后代入到公式 1 − 6 ∑ d i 2 n ( n 2 − 1 ) 1-\frac{6\sum{d_i^2}}{n(n^2-1)} 1−n(n2−1)6∑di2得到 r = 1 − 6 ∗ 194 10 ( 1 0 2 − 1 ) ≈ − 0.1758 r=1-\frac{6*194}{10(10^2-1)}\approx-0.1758 r=1−10(102−1)6∗194≈−0.1758。
简单公式只适用于 X i , Y i X_i,Y_i Xi,Yi中均无重复值的情况,任一列有重复值使用简单公式计算的结果就会有偏差。至于为什么有偏差,可以从下面(2)中的公式推导看出。
当有重复值时,一般采用平均顺序作为所有重复值的序号,例如对于序列[1, 1, 1, 2, 3],1的序号为(1+2+3)/3,均为2。原序列对应的序号为[2, 2, 2, 4, 5],经过验证在pandas的corr方法中采用的就是平均顺序计算。
(2)一般公式到简单公式的推导
推导可以从皮尔逊系数的计算公式2开始,只不过这里的 x i , y i x_i,y_i xi,yi代表的不是原值,而是原值对应的秩。下面推导过程中的前置条件为: x i , y i x_i,y_i xi,yi均服从类似1, 2, 3, 4, …这样的分布,均为正整数且不含重复值,因为这里的 x i , y i x_i,y_i xi,yi表示的是序号。这就要求原值中不能包含重复值。
ρ = 1 n ∑ i = 1 n x i y i − x ˉ y ˉ σ x σ y = 1 n ∑ i = 1 n 1 2 ( x i 2 + y i 2 − d i 2 ) − x ˉ 2 σ x σ y = 1 2 n ∑ i = 1 n x i 2 + 1 2 n ∑ i = 1 n y i 2 − 1 2 n ∑ i = 1 n d i 2 − x ˉ 2 σ x σ y = ( 1 n ∑ i = 1 n x i 2 − x ˉ 2 ) − 1 2 n ∑ i = 1 n d i 2 σ x σ y = σ x 2 − 1 2 n ∑ i = 1 n d i 2 σ x σ y = σ x σ y − 1 2 n ∑ i = 1 n d i 2 σ x σ y = 1 − 1 2 n ∑ i = 1 n d i 2 σ x σ y = 1 − 1 2 n ∑ i = 1 n d i 2 1 n ∑ i = 1 n x i 2 − x ˉ 2 \begin{aligned} \rho&=\frac{\frac1n\sum\limits_{i=1}^nx_iy_i-\bar{x}\bar{y}} {\sigma_x\sigma_y}\\ &=\frac{\frac1n\sum\limits_{i=1}^n\frac12(x_i^2+y_i^2-d_i^2)-\bar{x}^2} {\sigma_x\sigma_y}\\ &=\frac{\frac1{2n}\sum\limits_{i=1}^nx_i^2+\frac1{2n}\sum\limits_{i=1}^ny_i^2-\frac1{2n}\sum\limits_{i=1}^nd_i^2-\bar{x}^2} {\sigma_x\sigma_y}\\ &=\frac{(\frac1n\sum\limits_{i=1}^nx_i^2-\bar{x}^2)-\frac1{2n}\sum\limits_{i=1}^nd_i^2} {\sigma_x\sigma_y}\\ &=\frac{\sigma_x^2-\frac1{2n}\sum\limits_{i=1}^nd_i^2} {\sigma_x\sigma_y}\\ &=\frac{\sigma_x\sigma_y-\frac1{2n}\sum\limits_{i=1}^nd_i^2} {\sigma_x\sigma_y}\\ &=1-\frac{\frac1{2n}\sum\limits_{i=1}^nd_i^2} {\sigma_x\sigma_y}\\ &=1-\frac{\frac1{2n}\sum\limits_{i=1}^nd_i^2} {\frac1n\sum\limits_{i=1}^nx_i^2-\bar{x}^2} \end{aligned} ρ=σxσyn1i=1∑nxiyi−xˉyˉ=σxσyn1i=1∑n21(xi2+yi2−di2)−xˉ2=σxσy2n1i=1∑nxi2+2n1i=1∑nyi2−2n1i=1∑ndi2−xˉ2=σxσy(n1i=1∑nxi2−xˉ2)−2n1i=1∑ndi2=σxσyσx2−2n1i=1∑ndi2=σxσyσxσy−2n1i=1∑ndi2=1−σxσy2n1i=1∑ndi2=1−n1i=1∑nxi2−xˉ22n1i=1∑ndi2
其中 ∑ i = 1 n x i 2 = 1 2 + 2 2 + 3 2 + . . . + n 2 = n ( n + 1 ) ( 2 n + 1 ) 6 \sum\limits_{i=1}^nx_i^2=1^2+2^2+3^2+...+n^2=\frac{n(n+1)(2n+1)}{6} i=1∑nxi2=12+22+32+...+n2=6n(n+1)(2n+1)(金字塔数), x ˉ 2 = ( 1 + n 2 ) 2 \bar{x}^2=(\frac{1+n}{2})^2 xˉ2=(21+n)2,代入上面得到 ρ = 1 − 6 ∑ d i 2 n ( n 2 − 1 ) \rho=1-\frac{6\sum{d_i^2}}{n(n^2-1)} ρ=1−n(n2−1)6∑di2。
斯皮尔曼系数值域同样为[-1, 1],因为本身的计算还是基于皮尔逊系数公式。
参考https://en.wikipedia.org/wiki/Spearman%27s_rank_correlation_coefficient
五、卡方检验
皮尔逊系数和和斯皮尔曼系数都只适合度量数值型变量之间的相关关系,对于离散型的分类变量,可以通过卡方检验分析它们之间是否相互独立还是有相关关系。
下面随机生成100条数据,每条数据中均包含性别与是否打游戏这两个特征,基于此测试数据创建交叉表,统计不同性别中打游戏与不打游戏各自出现的频次。并基于交叉表进行卡方检验分析是否打游戏与性别之间是否存在关系。
首先提出零假设与备择假设:
- 零假设(H0):性别与是否打游戏之间没有联系
- 备择假设(H1):性别与是否打游戏之间存在联系
import pandas as pd
import numpy as np# 设置随机数种子并生成100条测试数据
np.random.seed(12)
data = {'性别': np.random.choice(['男', '女'], size=100),'是否打游戏': np.random.choice(['是', '否'], size=100)}
df = pd.DataFrame(data)# 创建交叉表
# margins、margins_name参数只是在频次结果的基础上增加个统计,这里是为了后续手工计算验证中方便对比,实际不需要带
frequency = pd.crosstab(df['性别'], df['是否打游戏'], margins=True, margins_name='总计')
frequency
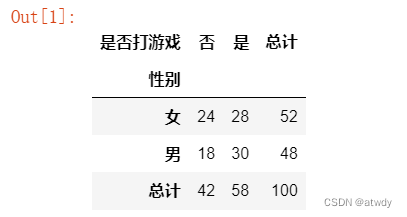
基于上面频次统计结果,进行卡方检验,分别获取卡方值、P值、自由度和期望频数。
from scipy.stats import chi2_contingency# 执行卡方检验,分别获取卡方值、P值、自由度和期望频数
# 该方法默认会对结果进行修正,correction参数设置为False是为了获取结果的原值方便后续对比
chi2, p, dof, expected = chi2_contingency(frequency.iloc[:2, :2], correction=False)
chi2, p, dof, expected

卡方值、P值、自由度分别为0.77、0.38、1。对结果的解读有两种方式:
- 实际分析中一般关注P值,若P值<0.05,则代表可以拒绝原假设,即分类变量间存在影响。这里P值为0.38,表示是否打游戏和性别之间可以认为存在联系。这里说下对P值的理解:指的是在原假设成立即分类变量间相互独立的情况下,当前观测值出现的概率。
- 也可以根据卡方值和自由度通过比对卡方分布表选择是否拒绝原假设。在卡方值分布表中通过自由度和自己选定的概率找到对应位置的卡方值,如果结果的卡方值比表中的卡方值大,则可以拒绝原假设,即分类变量间存在联系。卡方值可以理解成当分类变量间相互独立时的期望值与实际观测值之间的差异。后面会手工计算卡方值。
P值可以通过卡方值和自由度得到:
from scipy.stats import chi2# 输入卡方统计量和自由度
chi_square_value = 0.7673361121636983
degrees_of_freedom = 1# 计算P值
p_value = 1 - chi2.cdf(chi_square_value, degrees_of_freedom)
p
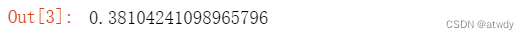
用Out[2]中的自由度和卡方值计算得到P值。
下面,手工计算一下卡方值。卡方值的计算过程为:
- 分别根据分类变量的类别组合统计各组合在观测值也就是实际数据中出现的频次,得到交叉表。
- 以分类变量相互间独立为前提,计算每个组合(即单元格)的期望频次。计算公式为:单元格所在行总和 × \times ×所在列总和 ÷ \div ÷样本总数。
- 通过公式 χ 2 = ∑ ( O i − E i ) 2 E i \chi^2=\sum\frac{(O_i-E_i)^2}{E_i} χ2=∑Ei(Oi−Ei)2计算卡方值,其中 O i , E i O_i,E_i Oi,Ei分别为每个单元格的观测频次和期望频次。
以测试数据的交叉表为例,性别为女、打游戏为否的这个单元格,期望频次=52*42/100=21.84, 同理按从上到下从左到右的顺序另外三个单元格的期望频次分别为30.16、20.16、27.84,符合代码中输出的期望值expected。
这里解释下期望频次的公式,还是以性别为女、打游戏为否的这个单元格为例,要理解这个公式,首先要明白一个前提就是假设分类变量间相互独立不存在影响。单元格所在的行和为52,表示100个样本中性别为女的样本有52个,所在列的和为42,表示100个样本中不打游戏的样本一共有42个,那么因为相互独立,所以性别为女且不打游戏的概率就应该等于样本中性别为女的概率乘样本中不打游戏的概率,最后再乘上总样本数量,就是在相互独立的情况下理论上的出现次数,即期望频次。
最后根据交叉表中的实际观测值和上面计算得到的期望值,通过步骤3中的公式得到卡方值。
def calc(o, e):return pow(o - e, 2) / echi2 = calc(24, 21.84) + calc(28, 30.16) + calc(18, 20.16) + calc(30, 27.84)
chi2

和卡方检验中输出的卡方值一致。但需要注意的是为了验证计算过程,在卡方检验中设置了参数correction=False,取消了方法中自带的误差修正,实际计算中应该取消设置。
卡方值大小受自由度影响,对于一个mxn的交叉表,自由度为(m-1)(n-1),从卡方值的计算过程可以看到,自由度越大,求和项越多,卡方值一般越大,但具体还受实际值与期望值之间差异的影响。
六、四分位法和箱线图
四分位法主要用来检测数据集中是否有离群值,箱线图可以认为是它的图形化表示。
四分位法需要首先对数据进行排序,排完序后再分别找出数据集中 1 4 \frac14 41位置处点的值(Q1)和 3 4 \frac34 43位置处点的值(Q3),得到四分位距(IQR)=Q3-Q1,进而得到离群值判定的阈值:
- 下界: Q 1 − 1.5 ∗ I Q R Q1-1.5*IQR Q1−1.5∗IQR
- 上界: Q 3 + 1.5 ∗ I Q R Q3+1.5*IQR Q3+1.5∗IQR
当数据集中的值不属于这个范围时,就可以认为是离群值。
具体怎么找出Q1与Q3,方法不唯一,这里以pandas中quantile方法的默认处理方式为例(API)。

例如对于有序序列[12, 15, 17, 20, 22, 25, 27, 30, 32, 35],元素个数n=10,需要找出它的第一四分位数(Q1),可以通过以下步骤:
- 计算Q1的位置。 ( n − 1 ) ∗ 1 4 + 1 = 3.25 (n-1)*\frac14+1=3.25 (n−1)∗41+1=3.25,大于3小于4,表示位置在第3个元素和第4个元素之间,更靠近第3个元素。
- Q 1 = V a l u e 3 + ( V a l u e 4 − V a l u e 3 ) ∗ 0.25 = 17 + ( 20 − 17 ) ∗ 0.25 = 17.75 Q1=Value_3+(Value_4-Value_3)*0.25=17+(20-17)*0.25=17.75 Q1=Value3+(Value4−Value3)∗0.25=17+(20−17)∗0.25=17.75,其中 V a l u e 3 , V a l u e 4 Value_3,Value_4 Value3,Value4分别表示第三个元素和第四个元素的值。从公式可以看出当位置处于两值之间时(也就是步骤1中结果为小数),Q1的结果是按照位置的权重在两值之间等比例增加的。
这里对步骤1中位置的计算方法进行下解释,因为刚开始我也有些迷惑。同一个数据集采用不同的计算方法可能会得到不同的位置结果。上面采用的方法中,是严格根据位置长度进行划分的。将10个数字有序排列,首尾数字之间9个间隔,那么 1 4 \frac14 41处的位置,就应该处于将整个长度四等分后的第一个等分点。因此应该等于 9 4 \frac94 49即2.25个长度。+1是因为对元素计数时是从第一个值开始数的,但是第二个值的位置才是第一个长度的位置。
代码验证也可以得到相同的结果:

下面,随机生成100个测试数据,其中包含5%的离群值和95%的正常值,然后通过四分位法找出这5个离群值。
import numpy as np
import pandas as pd# 设置随机数种子和数值以小数形式显示
np.random.seed(42)
np.set_printoptions(suppress=True)# 生成100个测试数据 返回50*2的二维数组
def get_data(size=100, outlier_percent=0.05):# 从服从均值为0,标准差为1的正态分布中抽取95%的样本量,大部分数据(99.7%)处于均值±3个标准差的范围内normal_data = np.random.normal(size=int(size*(1-outlier_percent)))# 从范围为[10,20]的均匀分布中抽取5%的样本量outlier_data = np.random.uniform(10, 20, size=int(size*outlier_percent))# 合并数据data = np.concatenate((normal_data, outlier_data))# 打散顺序np.random.shuffle(data)return data.reshape(size//2, 2)df = pd.DataFrame(get_data(), columns=list('AB'))# 计算 Q1 Q3 及四分位距IQR
Q1 = df.quantile(0.25)
Q3 = df.quantile(0.75)
IQR = Q3-Q1# 计算离群值阈值范围 获取离群值行索引和列索引
outlier_lower = Q1-1.5*IQR
outlier_upper = Q3+1.5*IQR
row, col = np.where((df < outlier_lower) | (df > outlier_upper))# 根据离群值行索引列索引,获取行号、列名及异常值
outlier = pd.DataFrame({'行号': df.index[row],'列名': df.columns[col],'离群值': df.values[row, col]
})
outlier

5个范围为[10, 20]的离群值都被找出,其中正态分布中的样本-2.619745也被识别为离群值,可以通过适当增大IQR的系数来调整。
下面通过箱线图查看测试数据的分布情况(箱线图API)。
import matplotlib.pyplot as plt# 设置中文和负号正常显示
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.sans-serif'] = ['SimHei']# 绘图输出,IQR系数默认为1.5,可以通过参数 whis 修改
plt.boxplot(df, labels=df.columns)
plt.show()
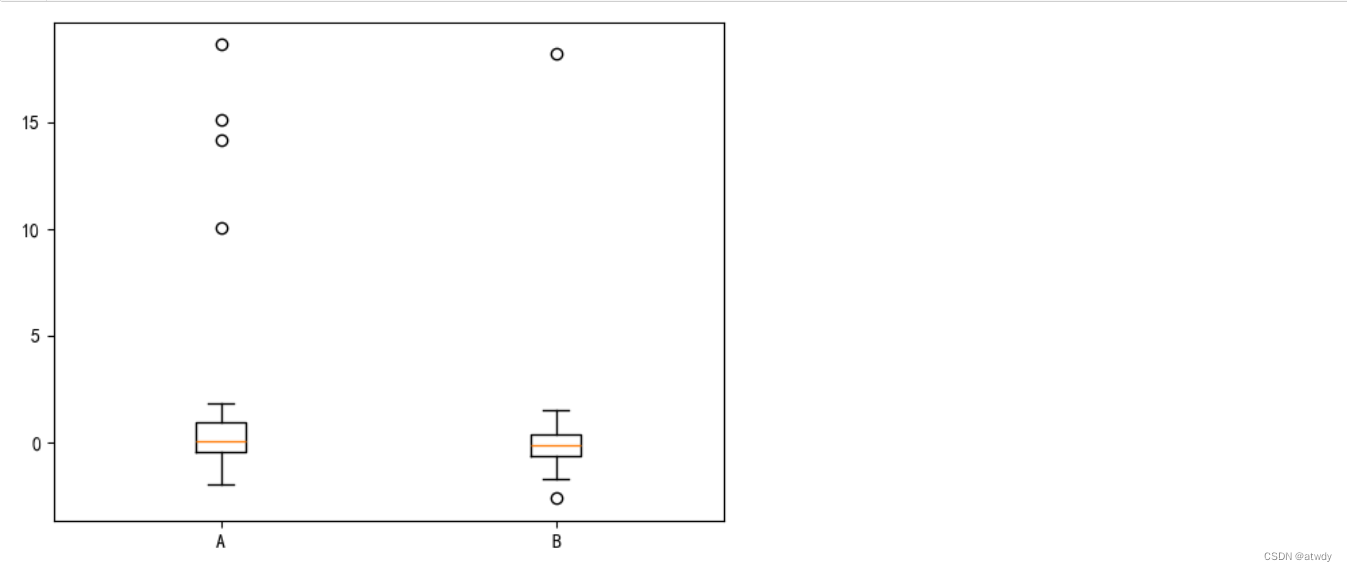
从图形中可以看到A列有4个离群值,均大于10,B列有2个离群值,一个大于10一个小于0。
矩形箱体表示数据中间50%的部分,箱体上下边界线和中间的线分别代表Q3、Q1和Q2(中位数),箱体两侧细线(须线)的端点处分别代表所有非离群值中的最大值和最小值,超出这个范围的被归类为离群值,用圆点表示。
根据图形的形状可以大致估计数据分布情况:
(1)箱体和两边须线的长度可以反映数据的分布情况是集中还是发散,越长越发散越短越集中。
(2)中位数在箱体中的位置可以大致了解数据分布是否对称。
(3)小圆点的位置和个数可以看出离群值所处的范围和数量。