题目：

给你一个非负整数数组 nums 和一个整数 target 。

向数组中的每个整数前添加 ‘+’ 或 ‘-’ ，然后串联起所有整数，可以构造一个 表达式

例如，nums = [2, 1] ，可以在 2 之前添加 ‘+’ ，在 1 之前添加 ‘-’ ，然后串联起来得到表达式 “+2-1” 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。

示例 1：

输入：

nums = [1,1,1,1,1], target = 3

输出：

5

解释：

一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3

示例 2：

输入：

nums = [1], target = 1

输出：

1

提示：

• 1 <= nums.length <= 20
• 0 <= nums[i] <= 1000
• 0 <= sum(nums[i]) <= 1000
• -1000 <= target <= 1000

思路：

本题可以用回溯来解决（但是会超时），也可以用动态规划中的01背包来解决，
如何转化为01背包问题呢。

假设加法的总和为x，那么减法对应的总和就是sum - x。

所以我们要求的是 x - (sum - x) = target

x = (target + sum) / 2

此时问题就转化为，装满容量为x的背包，有几种方法。

这里的x，就是bagSize，也就是我们后面要求的背包容量。

大家看到(target + sum) / 2 应该担心计算的过程中向下取整有没有影响。

这么担心就对了，例如sum 是5，S是2的话其实就是无解的，所以：

        # 如果nums的和与target的和的奇偶性不同，无法得到目标和为target的子集if (sum(nums) + target) % 2 == 1:return 0

同时如果 S的绝对值已经大于sum，那么也是没有方案的。

        # 如果目标和的绝对值大于nums的和，无法得到目标和为target的子集if abs(target) > sum(nums):return 0

再回归到01背包问题，为什么是01背包呢？

因为每个物品（题目中的1）只用一次

这次和之前遇到的背包问题不一样了，之前都是求容量为j的背包，最多能装多少。

本题则是装满有几种方法。其实这就是一个组合问题了。

动态规划五部曲：

1. 确定dp数组以及下标的含义

dp[j] 表示：填满j（包括j）这么大容积的包，有dp[j]种方法

2. 确定递推公式

有哪些来源可以推出dp[j]呢？

只要搞到nums[i]，凑成dp[j]就有dp[j - nums[i]] 种方法。

例如：dp[j]，j 为5，

• 已经有一个1（nums[i]） 的话，有 dp[4]种方法 凑成 dp[5]。
• 已经有一个2（nums[i]） 的话，有 dp[3]种方法 凑成 dp[5]。
• 已经有一个3（nums[i]） 的话，有 dp[2]中方法 凑成 dp[5]。
• 已经有一个4（nums[i]） 的话，有 dp[1]中方法 凑成 dp[5]。
• 已经有一个5（nums[i]） 的话，有 dp[0]中方法 凑成 dp[5]。

那么凑整dp[5]有多少方法呢，也就是把 所有的 dp[j - nums[i]] 累加起来。

dp[j] += dp[j - nums[i]]

这个跟爬楼梯（力扣：70爬楼梯）和不同路径（力扣：62.不同路径）的思路有点类似，现在在重新分析一下：
现在有dp[4]种方法凑成4,你手上还有一个数字1，那么凑成5的话有几种方法？ 还是dp[4]种方法！为什么不是dp[4] + 1 种方法呢？因为这个数字1是确定只能是+1，而不能是-1，只有一种方法使4变成5。可以这样理解，这里的方法数量最后是dp[4] * 1，
如果这里1可以是+1也可以是-1的话那方法数量应该是dp[4] * 2

同理，有dp[3]种方法凑成3，现在手上还有一个2，那么有几种方法凑成5？还是dp[3]种！

3. dp数组如何初始化

从递推公式可以看出，在初始化的时候dp[0] 一定要初始化为1，因为dp[0]是在公式中一切递推结果的起源，如果dp[0]是0的话，递推结果将都是0。

这里有录友可能认为从dp数组定义来说 dp[0] 应该是0，也有录友认为dp[0]应该是1。

其实不要硬去解释它的含义，咱就把 dp[0]的情况带入本题看看应该等于多少。

如果数组[0] ，target = 0，那么 bagSize = (target + sum) / 2 = 0。 dp[0]也应该是1， 也就是说给数组里的元素 0 前面无论放加法还是减法，都是 1 种方法。

所以本题我们应该初始化 dp[0] 为 1。

4. 确定遍历顺序

毋庸置疑，对于01背包问题一维dp的遍历，nums放在外循环，target在内循环，且内循环倒序。

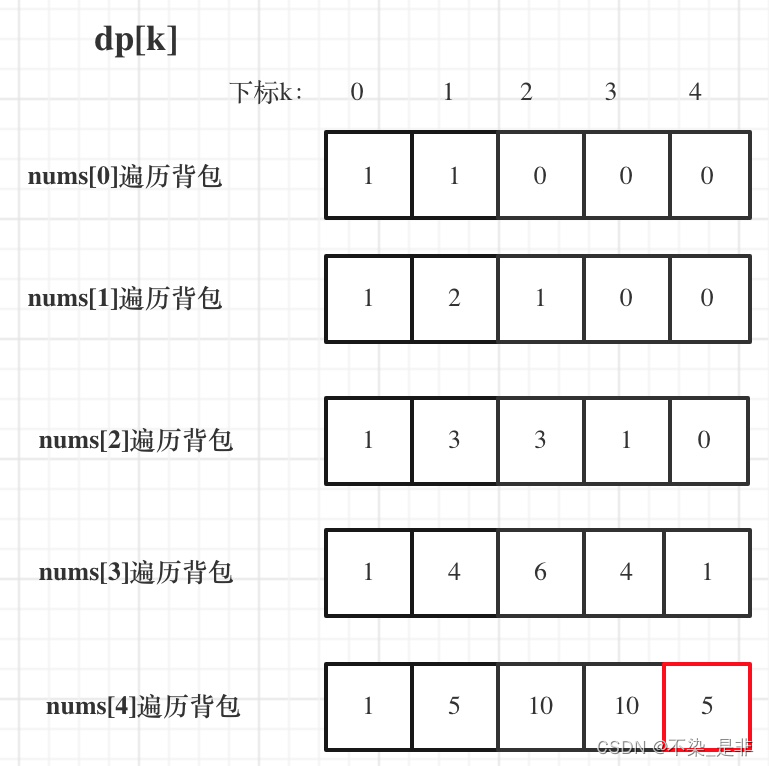
5. 举例推导dp数组

输入：nums: [1, 1, 1, 1, 1], S: 3

bagSize = (S + sum) / 2 = (3 + 5) / 2 = 4

dp数组状态变化如下：

代码及详细注释：

一维dp数组：

class Solution:def findTargetSumWays(self, nums: List[int], target: int) -> int:# 如果nums的和与target的和的奇偶性不同，无法得到目标和为target的子集if (sum(nums) + target) % 2 == 1:return 0# 如果目标和的绝对值大于nums的和，无法得到目标和为target的子集if abs(target) > sum(nums):return 0# 计算S，S为目标和S = (target + sum(nums)) // 2# 创建一个长度为S+1的数组dp，用于记录可以得到和为i的子集的个数dp = [0] * (S + 1)dp[0] = 1  # 初始化dp[0]为1# 遍历nums中的每个数字for i in range(len(nums)):# 从S到nums[i]遍历，更新dp数组for j in range(S, nums[i] - 1, -1):# 更新dp[j]的值dp[j] += dp[j - nums[i]]# 返回dp[S]，表示可以得到和为S的子集的个数return dp[S]

• 时间复杂度：O(n × m)，n为正数个数，m为背包容量
• 空间复杂度：O(m)，m为背包容量

回溯版本：

class Solution:def backtracking(self, candidates, target, total, startIndex, path, result):if total == target:result.append(path[:])  # 将当前路径的副本添加到结果中# 如果 sum + candidates[i] > target，则停止遍历for i in range(startIndex, len(candidates)):if total + candidates[i] > target:breaktotal += candidates[i]path.append(candidates[i])self.backtracking(candidates, target, total, i + 1, path, result)total -= candidates[i]path.pop()def findTargetSumWays(self, nums: List[int], target: int) -> int:total = sum(nums)if target > total:return 0  # 此时没有方案if (target + total) % 2 != 0:return 0  # 此时没有方案，两个整数相加时要注意数值溢出的问题bagSize = (target + total) // 2  # 转化为组合总和问题，bagSize就是目标和# 以下是回溯法代码result = []nums.sort()  # 需要对nums进行排序self.backtracking(nums, bagSize, 0, 0, [], result)return len(result)