文章目录
- 参考内容
- lam=0.1
- lam=3
- lam=10
- lam=50
- lam=100
- lam=300
- 画图
- 线性规划
- matlab
- python代码
参考内容
https://blog.csdn.net/qq_41129489/article/details/128830589
https://zhuanlan.zhihu.com/p/542379144
我主要想强调的是这个例子的解法存在的一些细节问题
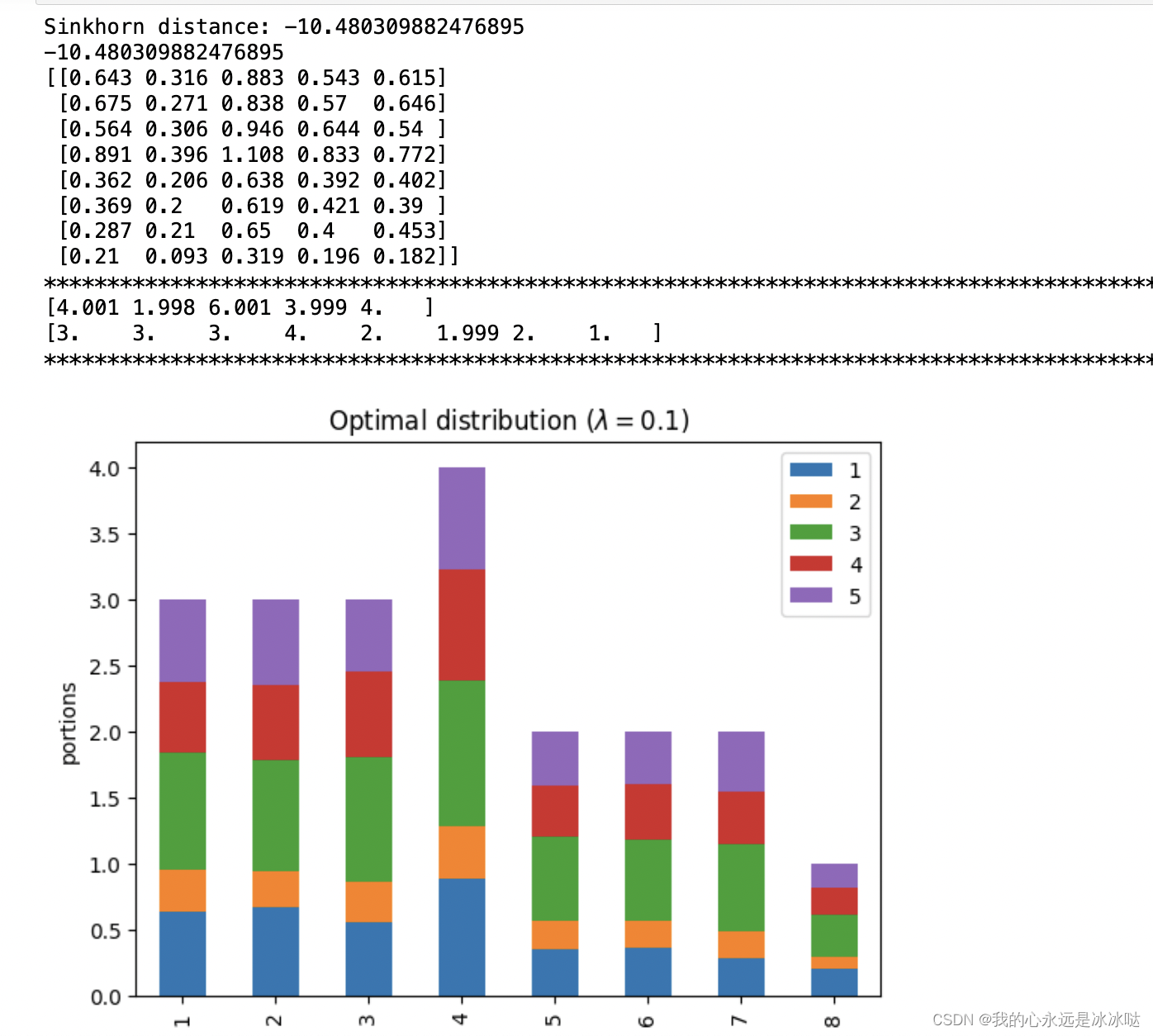
lam=0.1
lam = 0.1P, d = compute_optimal_transport(M,r,c, lam=lam)partition = pd.DataFrame(P, index=np.arange(1, 9), columns=np.arange(1, 6))
ax = partition.plot(kind='bar', stacked=True)
print('Sinkhorn distance: {}'.format(d))
ax.set_ylabel('portions')
ax.set_title('Optimal distribution ($\lambda={}$)'.format(lam))print(d)PP = np.around(P,3)
print(PP)print("*"*100)
print(np.sum(PP,axis=0))
print(np.sum(PP,axis=1))
print("*"*100)
## 这个很接近了
结果如下
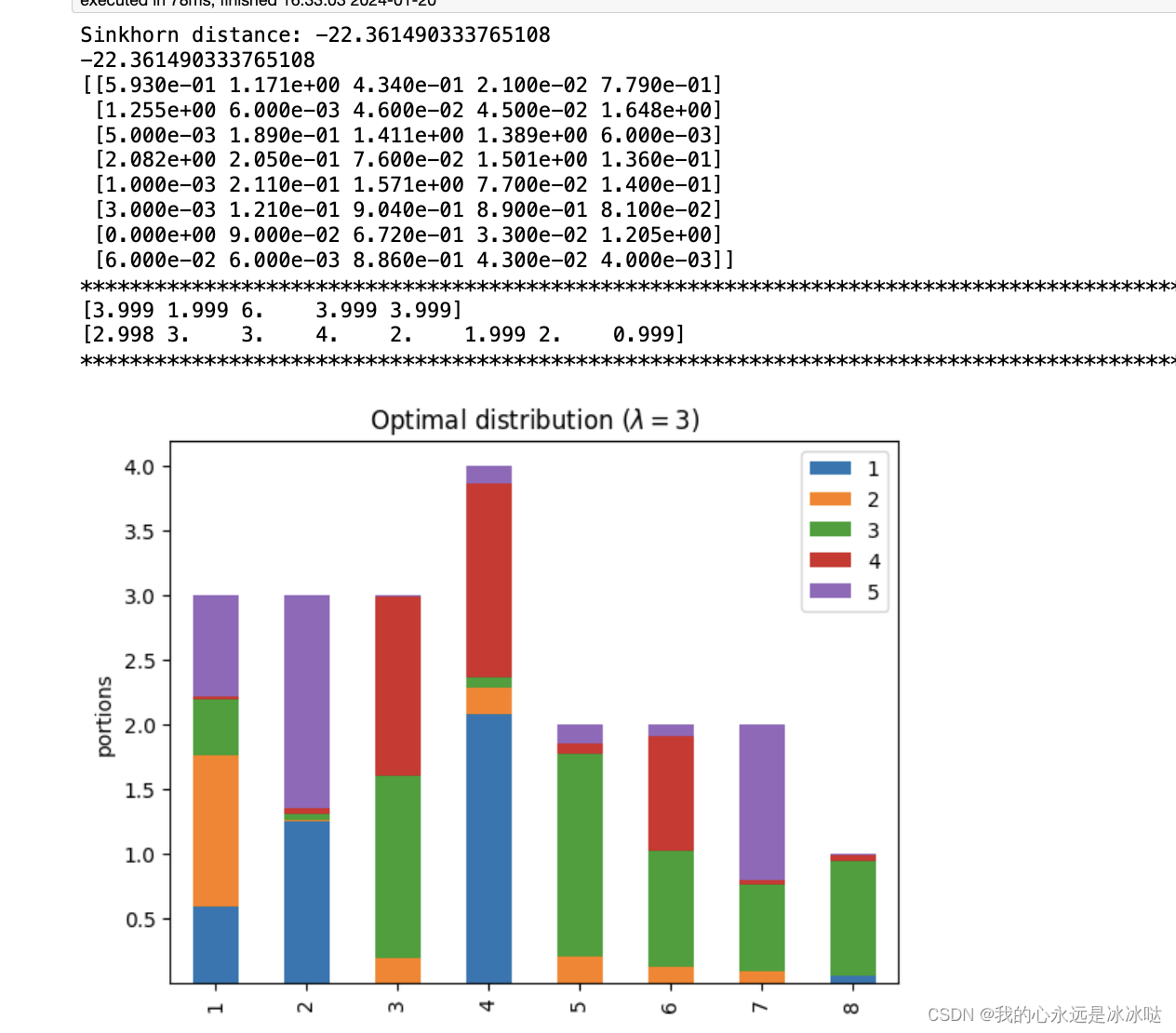
lam=3
lam = 3P, d = compute_optimal_transport(M,r,c, lam=lam)partition = pd.DataFrame(P, index=np.arange(1, 9), columns=np.arange(1, 6))
ax = partition.plot(kind='bar', stacked=True)
print('Sinkhorn distance: {}'.format(d))
ax.set_ylabel('portions')
ax.set_title('Optimal distribution ($\lambda={}$)'.format(lam))
print(d)PP = np.around(P,3)
print(PP)print("*"*100)
print(np.sum(PP,axis=0))
print(np.sum(PP,axis=1))
print("*"*100)
## 这个很接近了
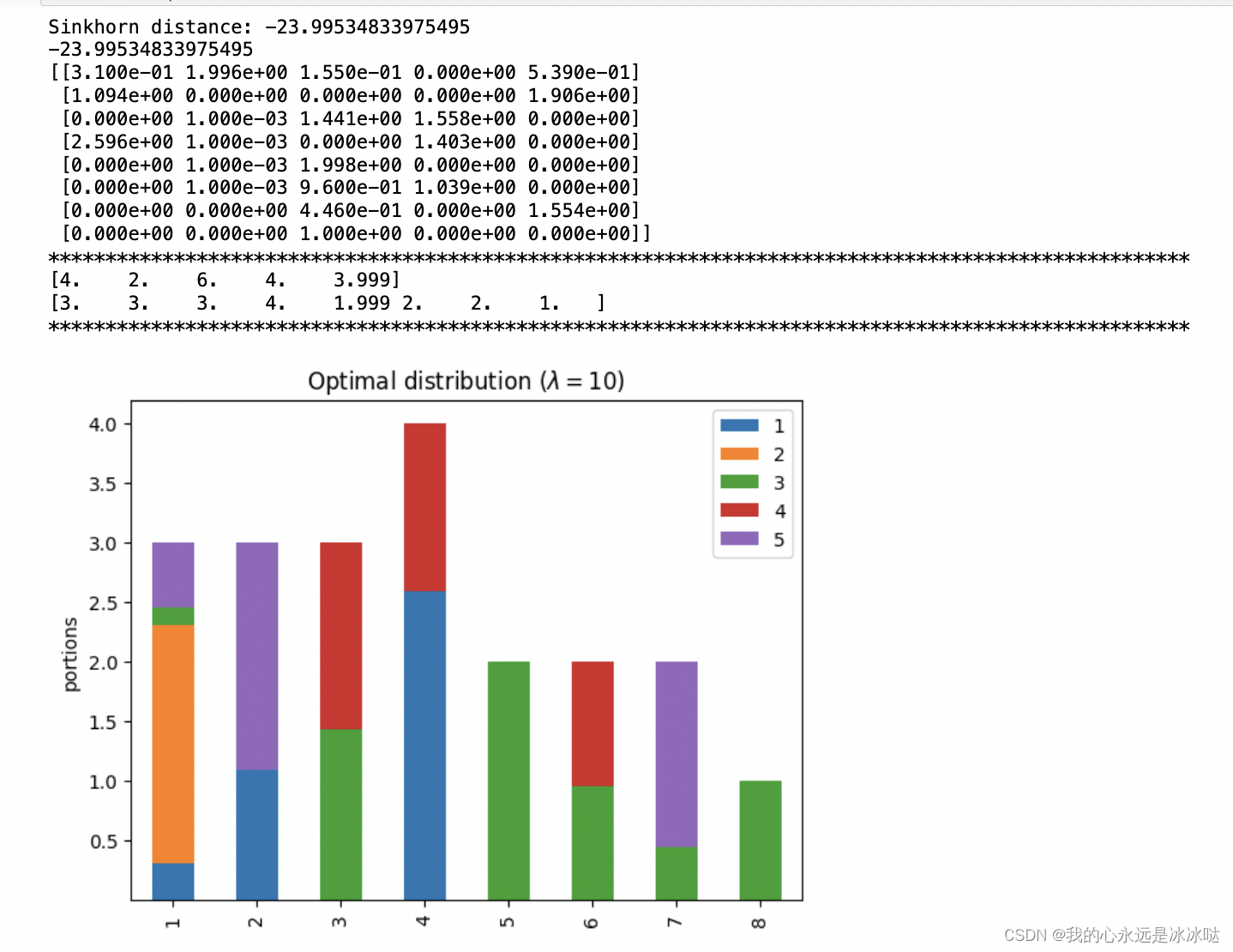
lam=10
lam = 10P, d = compute_optimal_transport(M,r,c, lam=lam)partition = pd.DataFrame(P, index=np.arange(1, 9), columns=np.arange(1, 6))
ax = partition.plot(kind='bar', stacked=True)
print('Sinkhorn distance: {}'.format(d))
ax.set_ylabel('portions')
ax.set_title('Optimal distribution ($\lambda={}$)'.format(lam))print(d)PP = np.around(P,3)
print(PP)print("*"*100)
print(np.sum(PP,axis=0))
print(np.sum(PP,axis=1))
print("*"*100)
## 这个很接近了
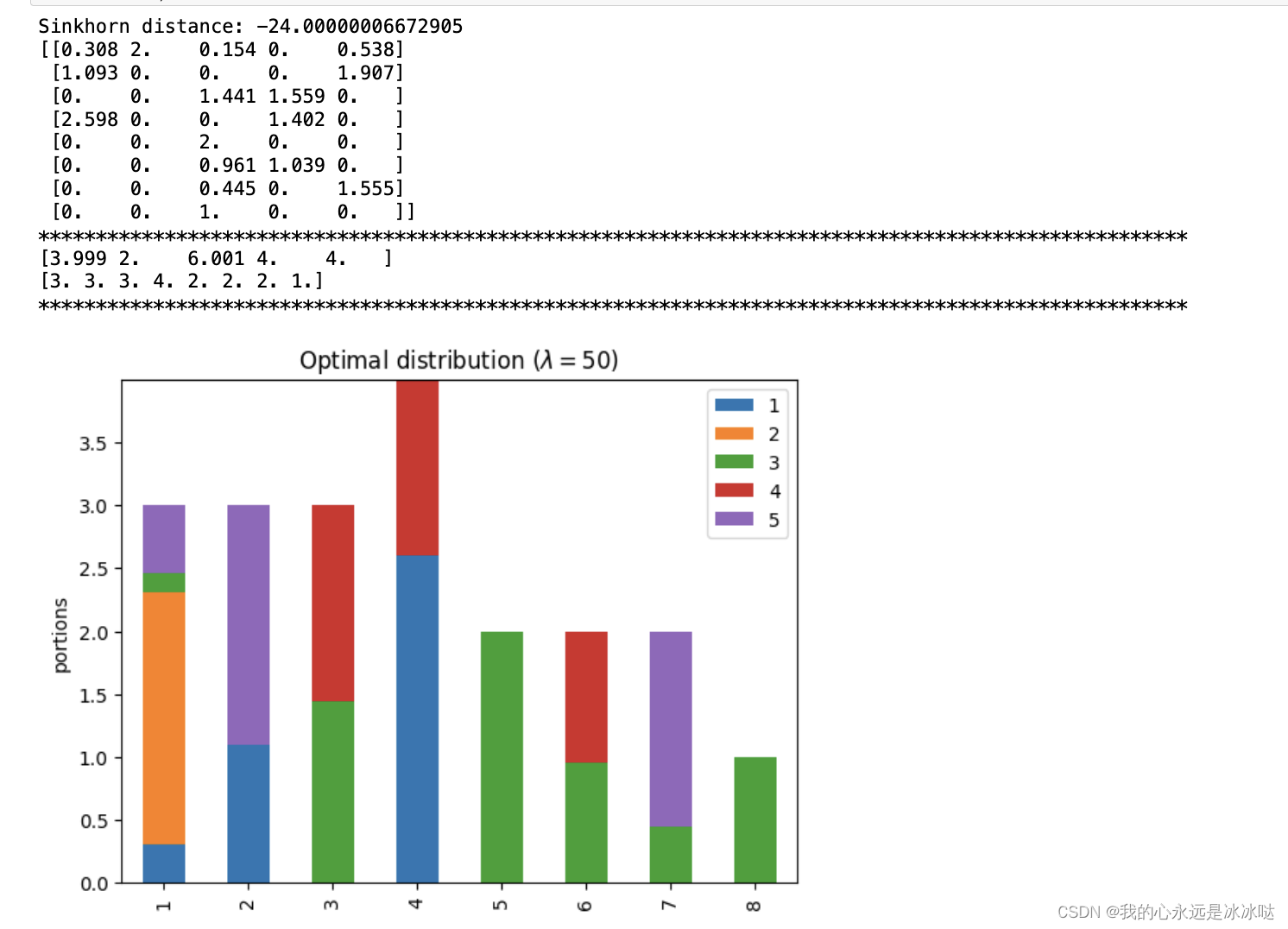
lam=50
lam = 50P, d = compute_optimal_transport(M,r,c, lam=lam)partition = pd.DataFrame(P, index=np.arange(1, 9), columns=np.arange(1, 6))
ax = partition.plot(kind='bar', stacked=True)
print('Sinkhorn distance: {}'.format(d))
ax.set_ylabel('portions')
ax.set_title('Optimal distribution ($\lambda={}$)'.format(lam))PP = np.around(P,3)
print(PP)print("*"*100)
print(np.sum(PP,axis=0))
print(np.sum(PP,axis=1))
print("*"*100)
## 这个很接近了
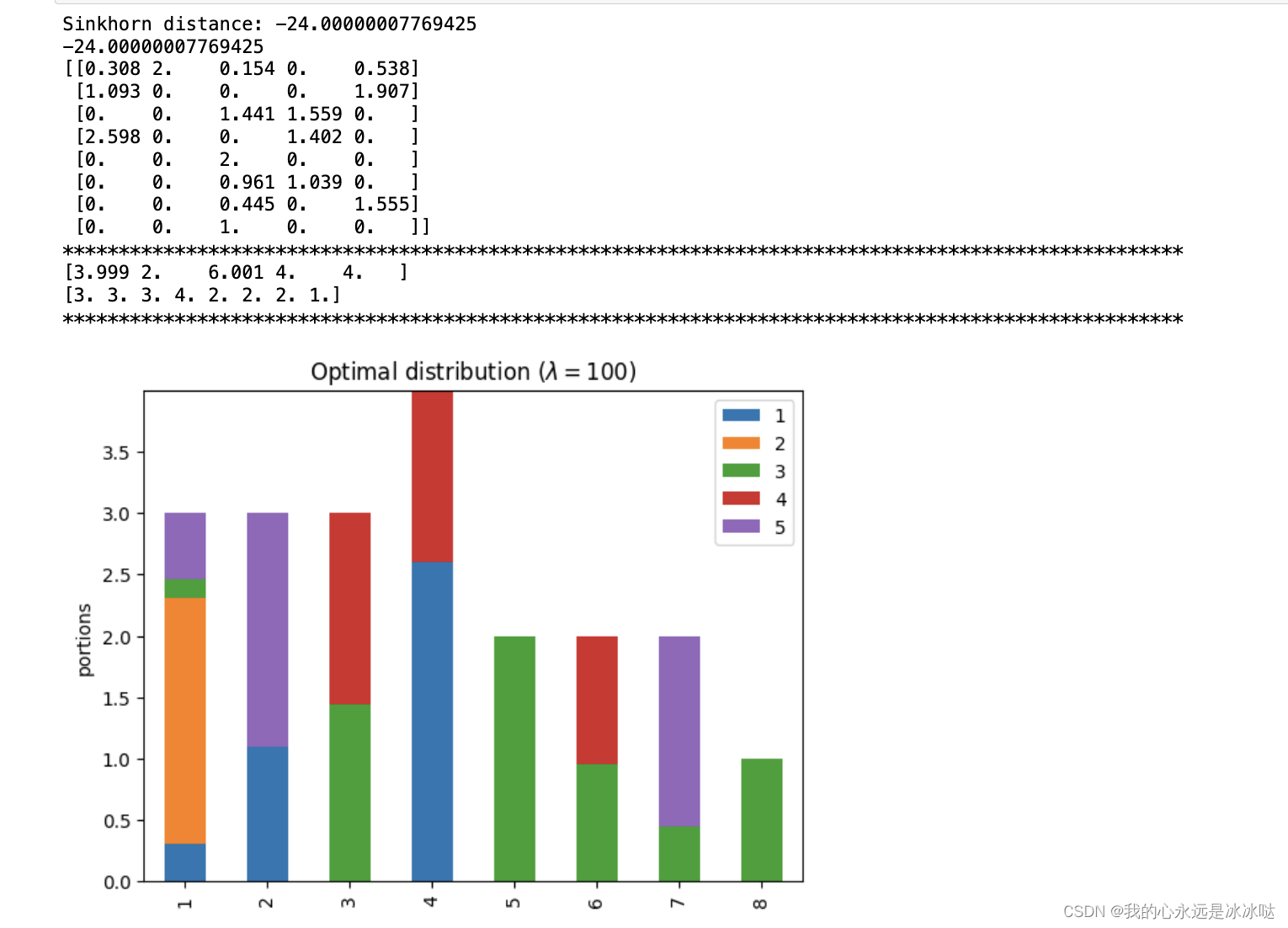
lam=100
lam = 100P, d = compute_optimal_transport(M,r,c, lam=lam)partition = pd.DataFrame(P, index=np.arange(1, 9), columns=np.arange(1, 6))
ax = partition.plot(kind='bar', stacked=True)
print('Sinkhorn distance: {}'.format(d))
ax.set_ylabel('portions')
ax.set_title('Optimal distribution ($\lambda={}$)'.format(lam))print(d)
PP = np.around(P,3)
print(PP)print("*"*100)
print(np.sum(PP,axis=0))
print(np.sum(PP,axis=1))
print("*"*100)
## 这个很接近了
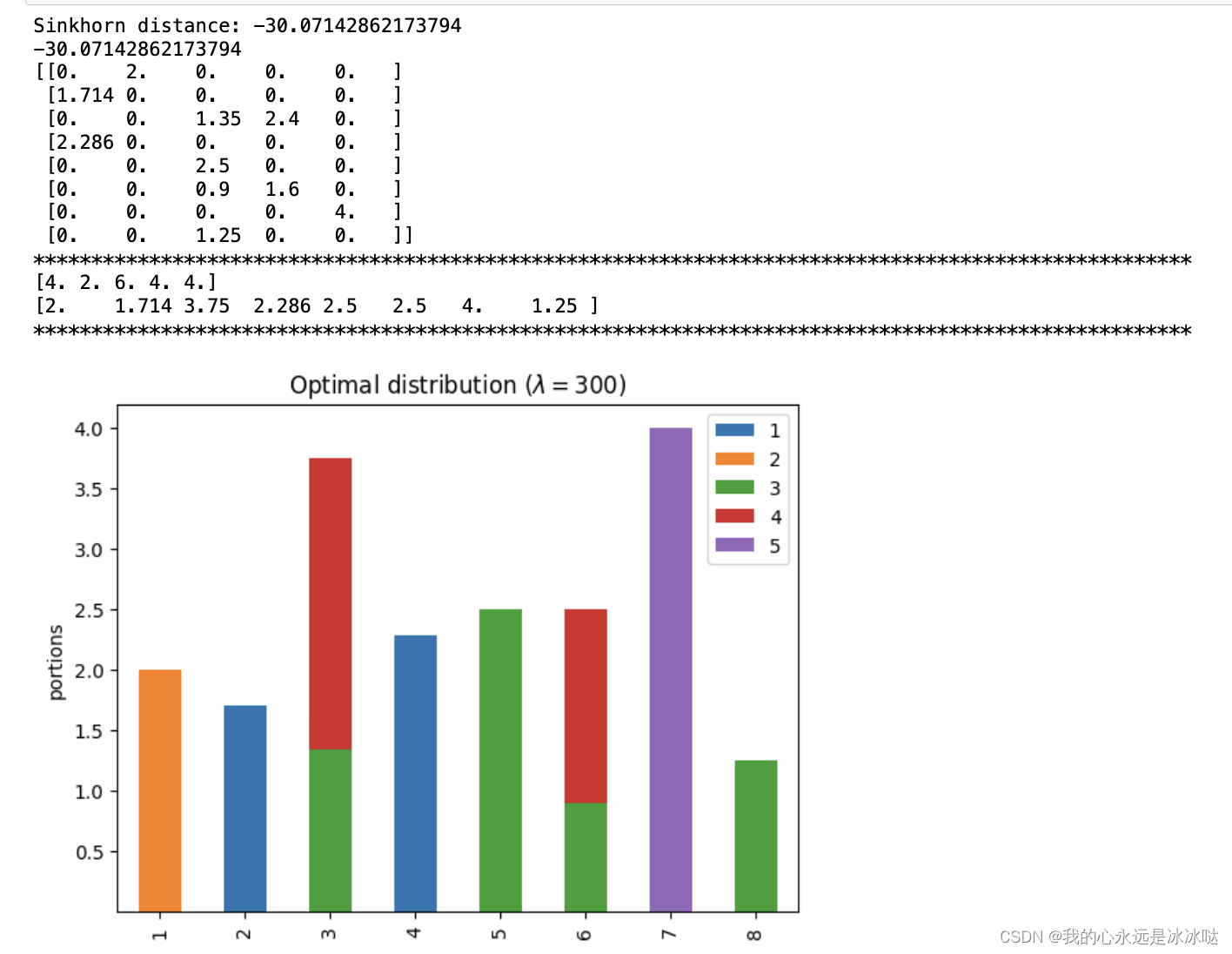
lam=300
lam = 300P, d = compute_optimal_transport(M,r,c, lam=lam)partition = pd.DataFrame(P, index=np.arange(1, 9), columns=np.arange(1, 6))
ax = partition.plot(kind='bar', stacked=True)
print('Sinkhorn distance: {}'.format(d))
ax.set_ylabel('portions')
ax.set_title('Optimal distribution ($\lambda={}$)'.format(lam))print(d)
PP = np.around(P,3)
print(PP)print("*"*100)
print(np.sum(PP,axis=0))
print(np.sum(PP,axis=1))
print("*"*100)
## 这个就不接近了,之前的求和都是相差在0.001左右,可以近似看作相等
## 但是这个行和是 [2. 1.714 3.75 2.286 2.5 2.5 4. 1.25 ]
## 很明显是 [3. 3. 3. 4. 2. 2. 2. 1.]这个是不对的,所以lam=300时这个值已经发散了,
## 虽然此时的Sinkhorn distance是小于24的,但也不起作用
画图
import numpy as np
import pandas as pd
import matplotlib.pyplot as pltdef compute_optimal_transport(M=None, r=None, c=None, lam=None, eplison=1e-8):"""Computes the optimal transport matrix and Slinkhorn distance using theSinkhorn-Knopp algorithmInputs:- M : cost matrix (n x m)- r : vector of marginals (n, )- c : vector of marginals (m, )- lam : strength of the entropic regularization- epsilon : convergence parameterOutputs:- P : optimal transport matrix (n x m)- dist : Sinkhorn distance"""r = np.array([3, 3, 3, 4, 2, 2, 2, 1])c = np.array([4, 2, 6, 4, 4])M = np.array([[2, 2, 1, 0, 0], [0, -2, -2, -2, -2], [1, 2, 2, 2, -1], [2, 1, 0, 1, -1],[0.5, 2, 2, 1, 0], [0, 1, 1, 1, -1], [-2, 2, 2, 1, 1], [2, 1, 2, 1, -1]],dtype=float) M = -M # 将M变号,从偏好转为代价n, m = M.shape # 8, 5P = np.exp(-lam * M) # (8, 5)P /= P.sum() # 归一化u = np.zeros(n) # (8, )# normalize this matrixwhile np.max(np.abs(u - P.sum(1))) > eplison: # 这里是用行和判断收敛# 对行和列进行缩放,使用到了numpy的广播机制,不了解广播机制的同学可以去百度一下u = P.sum(1) # 行和 (8, )P *= (r / u).reshape((-1, 1)) # 缩放行元素,使行和逼近rv = P.sum(0) # 列和 (5, )P *= (c / v).reshape((1, -1)) # 缩放列元素,使列和逼近creturn P, np.sum(P * M) # 返回分配矩阵和Sinkhorn距离lam_list=[1,5,10,20,30,40,50,60,70,80,90,100,110,120,130,140,150]cost_list=[]
for lam in lam_list:P, d = compute_optimal_transport(lam=lam)cost_list.append(d)
print(cost_list)
plt.plot(np.array(lam_list),np.array(cost_list),c="g")
plt.show()## 现在这个地方也有的
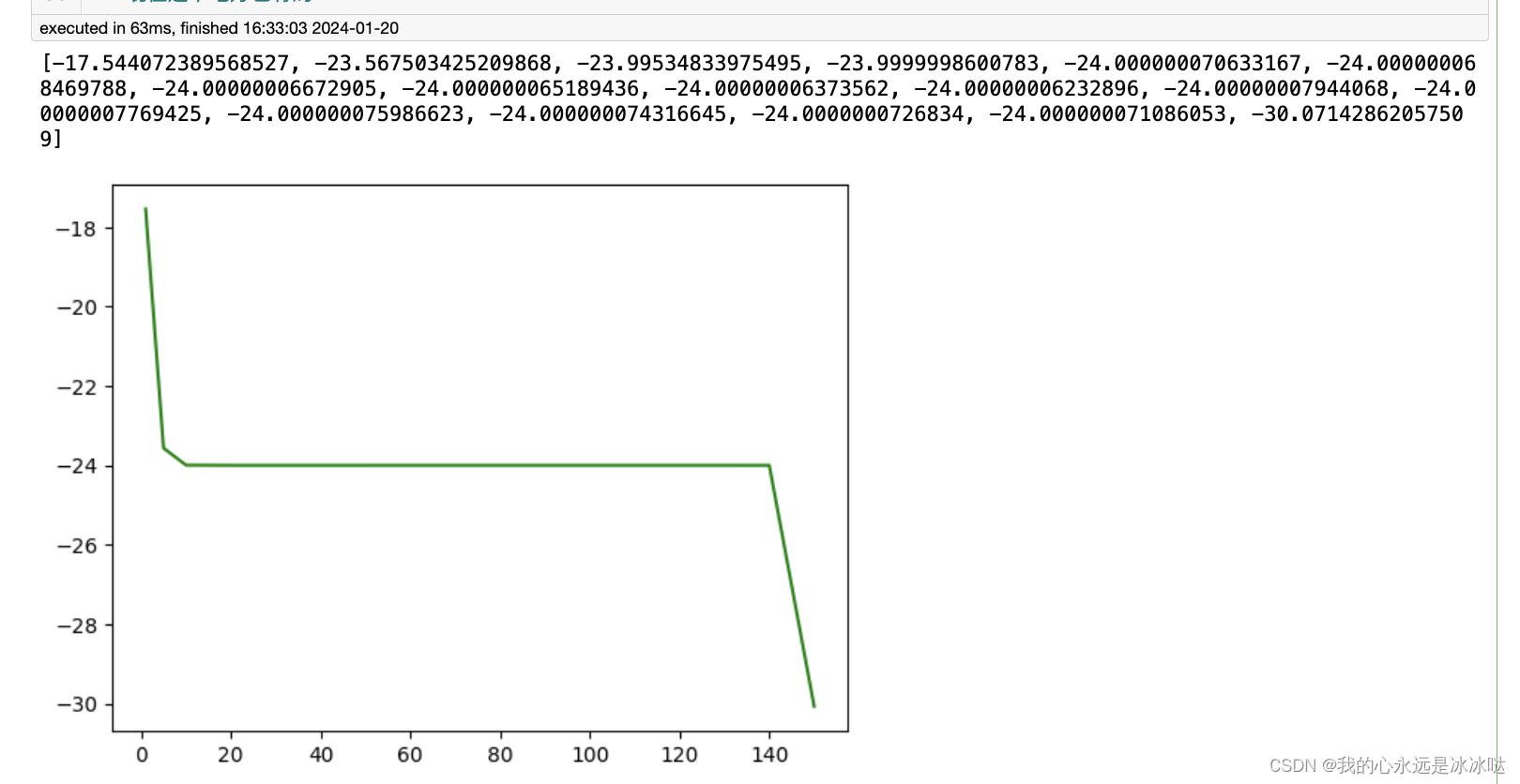
这个地方其实有一个画图的小问题,我待会要再写一下
可以看到大概是在lam =150的时候,就已经不稳定了,所以这个例子的问题的解的最小花费约等于24,但是我发现一个更有意思的问题,就是这个分配矩阵是唯一的吗,很显然不是的, 利用我上篇文章学到的线性规划,我发现matlab和python找到的是两个不同的解,
线性规划
matlab
clc;
clear;r = [3, 3, 3, 4, 2, 2, 2, 1];
c = [4, 2, 6, 4, 4];
cost_matrix = [2, 2, 1, 0, 0;0, -2, -2, -2, -2; 1, 2, 2, 2, -1;2, 1, 0, 1, -1;0.5, 2, 2, 1, 0;0, 1, 1, 1, -1;-2, 2, 2, 1, 1;2, 1, 2, 1, -1];cost_matrix_t = (-1)*transpose(cost_matrix);% 需要有符号
cost_vec = cost_matrix_t(:);raw_equ = zeros(8,40);
for i =1:8raw_equ(i,((i-1)*5+1):((i-1)*5+5))=1;
endcol_equ = zeros(5,40);
for i =1:5for j =1:8col_equ(i,i+(j-1)*5)=1;end
endequ = [raw_equ;col_equ];
equ_value = horzcat(r, c);
% x1,x2,x3,x4,x5
% x6,x7,x8,x9,x10
% x11,x12,x13,x14,x15
% x16,x17,x18,x19,x20
% x21,x22,x23,x24,x25
% x26,x27,x28,x29,x30
% x31,x32,x33,x34,x35
% x36,x37,x38,x39,x40% 现在我要求的变量是这样的,
f=cost_vec; % 价值向量
a=[]; % a、b对应不等式的左边和右边
b=[];
aeq=equ; % aeq和beq对应等式的左边和右边
beq=equ_value;
[x,y]=linprog(f,a,b,aeq,beq,zeros(40,1));arr_mat = transpose(reshape(x',5,8));结果如下
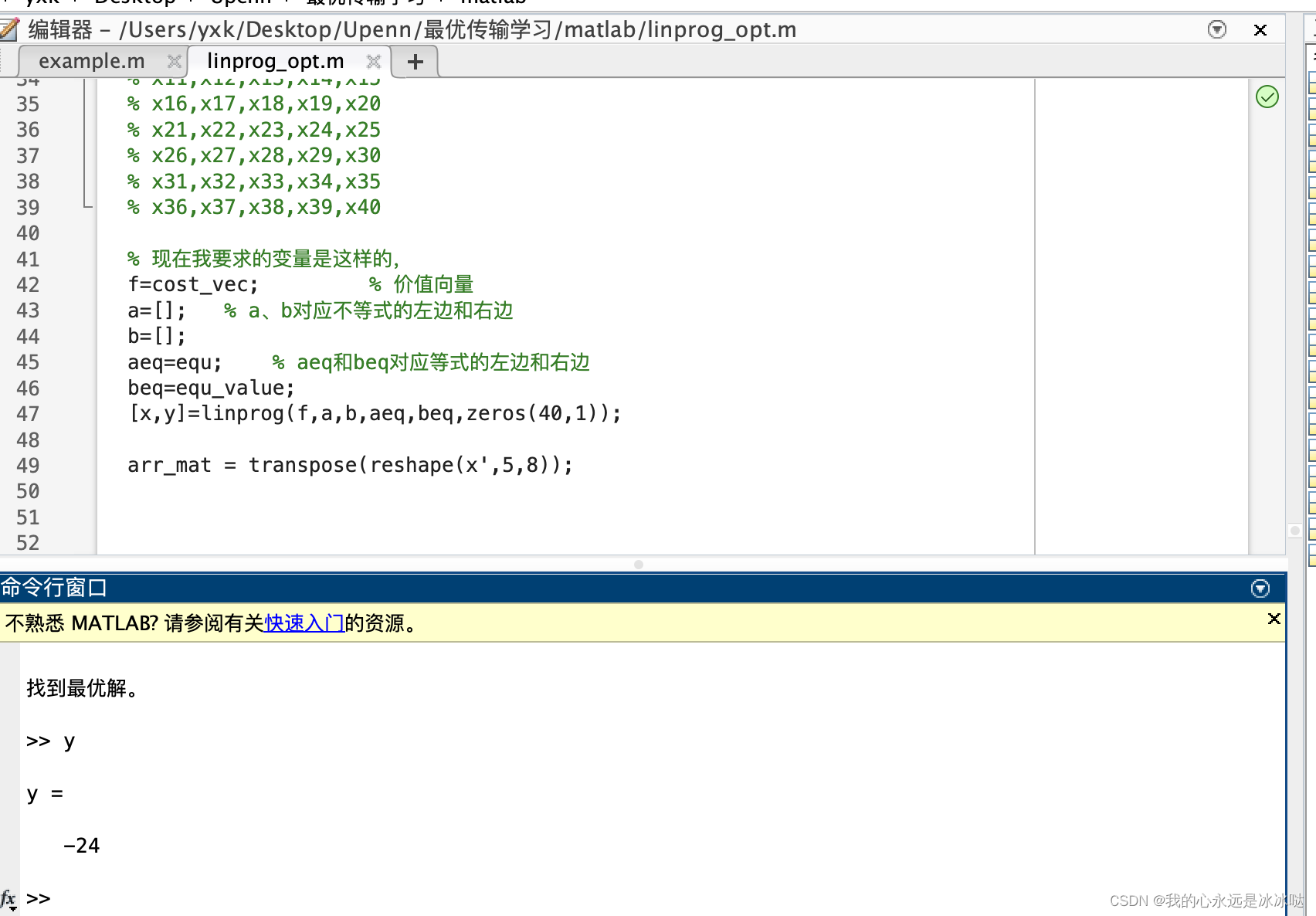
分配矩阵如下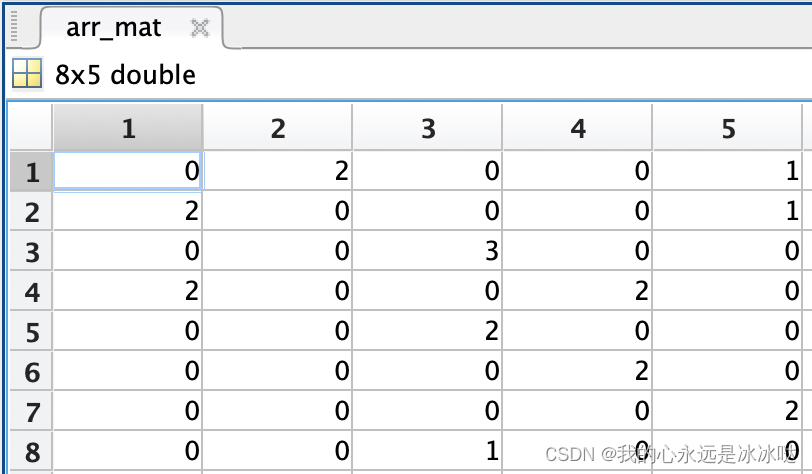
python代码
# Define parameters
m = 8
n = 5p = np.array([3, 3, 3, 4, 2, 2, 2, 1])
q = np.array([4, 2, 6, 4, 4])C = -1*np.array([[2, 2, 1, 0, 0], [0, -2, -2, -2, -2], [1, 2, 2, 2, -1], [2, 1, 0, 1, -1],[0.5, 2, 2, 1, 0], [0, 1, 1, 1, -1], [-2, 2, 2, 1, 1], [2, 1, 2, 1, -1]],dtype=float)# Vectorize matrix C
C_vec = C.reshape((m*n, 1), order='F')# Construct matrix A by Kronecker product
A1 = np.kron(np.ones((1, n)), np.identity(m))
A2 = np.kron(np.identity(n), np.ones((1, m)))
A = np.vstack([A1, A2])# Construct vector b
b = np.hstack([p, q])# Solve the primal problem
res = linprog(C_vec, A_eq=A, b_eq=b)# Print results
print("message:", res.message)
print("nit:", res.nit)
print("fun:", res.fun)
print("z:", res.x)
print("X:", res.x.reshape((m,n), order='F'))
结果如下
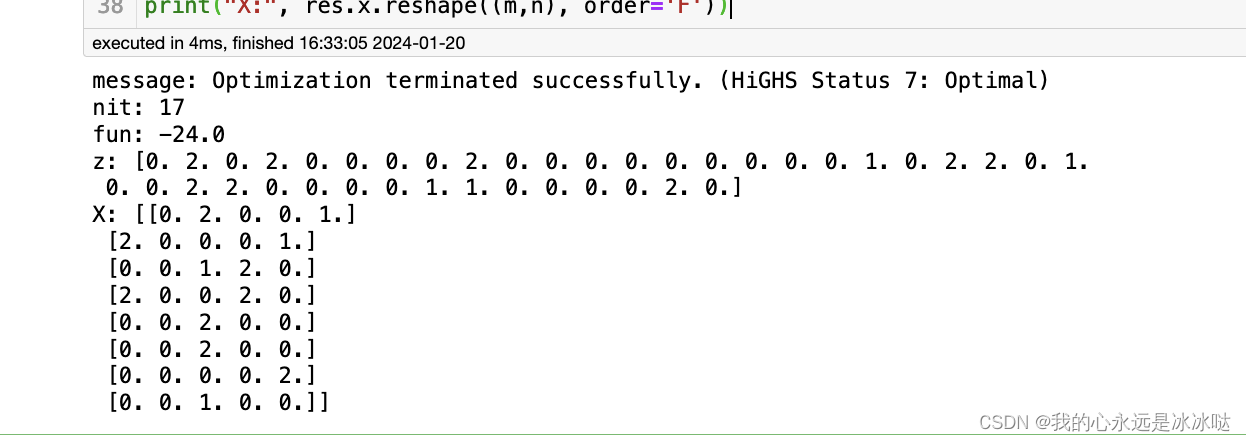
可以看到花费都是24,但是两者的分配矩阵并不一样哈