【数据结构】二叉树相关oj题（一）-编程知识

1、二叉树的构建及遍历

1.1、题目介绍

1.2、解题思路

1.3、代码描述

1.4、完整代码

2、二叉树的层次遍历

2.1、题目介绍

2.2、解题思路

2.3、代码描述

2.4、完整代码

1、二叉树的构建及遍历

1.1、题目介绍

原题链接：KY11 二叉树构建及遍历_牛客题霸_牛客网 (nowcoder.com)

示例1：

输入：abc##de#g##f###

输出：c b e g d f a

1.2、解题思路

根据题意可知，读入的字符串是一串先序遍历字符串，那么根据字符串创建二叉树也就需要遵循先序遍历进行创建。

1.3、代码描述

首先自行定义一个TreeNode类

class TreeNode {public char val;public TreeNode left;public TreeNode right;public TreeNode(char val) {this.val = val;}
}

因为递归创建，为了确保str能够正常遍历结束，因此这里定义一个成员变量 i 用于记录str当前访问的位置。

char ch = str.charAt(i++); 此时当ch不为#时再创建节点root，并且对左孩子和右孩子分别进行递归创建。

    public static int i = 0;public static TreeNode createTree(String str) {if(str == null) {return null;}TreeNode root = null;char ch = str.charAt(i++);if(ch != '#') {root = new TreeNode(ch);root.left = createTree(str);root.right = createTree(str);} return root;}

最后执行中序遍历将结果打印出来即可

    public static void inOrder(TreeNode root) {if(root == null) {return;}inOrder(root.left);System.out.print(root.val + " ");inOrder(root.right);}

1.4、完整代码

import java.util.Scanner;class TreeNode {public char val;public TreeNode left;public TreeNode right;public TreeNode(char val) {this.val = val;}
}// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {public static void main(String[] args) {Scanner in = new Scanner(System.in);String str = in.nextLine();//创建二叉树TreeNode root = createTree(str);//中序遍历二叉树inOrder(root);}public static int i = 0;public static TreeNode createTree(String str) {if(str == null) {return null;}TreeNode root = null;char ch = str.charAt(i++);if(ch != '#') {root = new TreeNode(ch);root.left = createTree(str);root.right = createTree(str);} return root;}public static void inOrder(TreeNode root) {if(root == null) {return;}inOrder(root.left);System.out.print(root.val + " ");inOrder(root.right);}
}

2、二叉树的层次遍历

2.1、题目介绍

原题链接：102. 二叉树的层序遍历 - 力扣（LeetCode）

示例1：

输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例2：

输入：root = [1]
输出：[[1]]

示例3：

输入：root = []
输出：[]

提示：

树中节点数目在范围 [0, 2000] 内
-1000 <= Node.val <= 1000

2.2、解题思路

层次遍历需要使用到队列，利用队列先进先出的特性使遍历能够从上到下，从左到右顺序遍历。该题唯一的难点就是返回值的规范。

题目中要求返回的是List<List<Integer>>，从示例中可以看出，每一层的节点分别使用有一个List来存储，这就要求我们不仅需要实现层序遍历，还需要将遍历结果按照层数划分。

2.3、代码描述

首先实现层次遍历，判断root不等于null后执行以下代码，将root入队之后，观察队列状况，当队列不为空时将节点出队，并判断出队节点是否存在左右节点，如果存在则入队。依次执行循环后最终得到打印结果就为层次遍历结果。

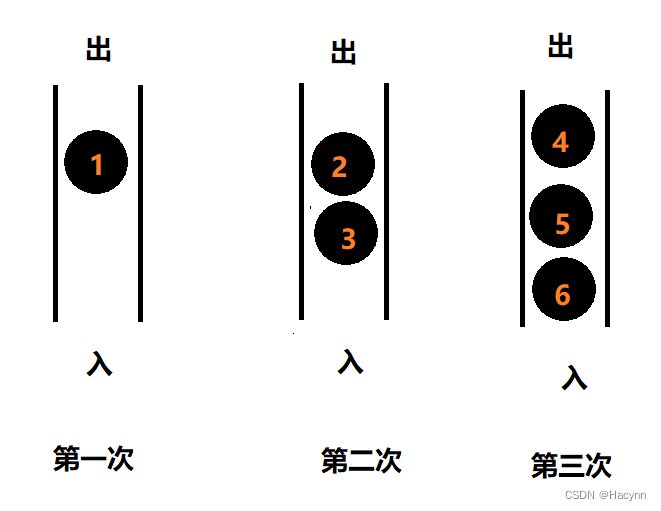
        Queue<TreeNode> queue = new LinkedList<>();queue.add(root);while(!queue.isEmpty()) {TreeNode cur = queue.poll();//此处对cur.val执行打印操作，打印的顺序就是层次遍历顺序System.out.print(root.val + " ");if(cur.left != null) {queue.add(cur.left);}if(cur.right != null) {queue.add(cur.right);}}

假设二叉树的结构如下：

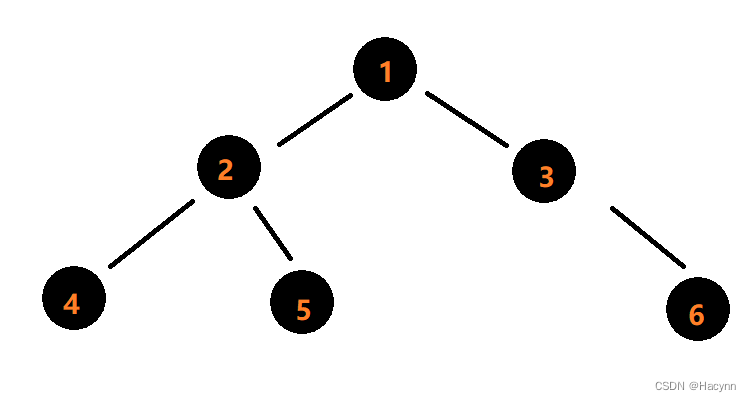
通过画图可以观察到，当将1入队后，此时队长为1。然后1出队后将2，3入队，此时队长为2。然后2出队4，5入队，3出队6入队，此时队长为3。

相信大家都看出规律了，即每当执行完一组入队操作之后，此时队列的长度就等于层数个数。根据这个规律，我们可以在每次while循环的开始计算此时队列的长度，用于记录该层需要出队的次数，从而确定每一层的节点，并将其存放到list中，最后当while循环结束时将list添加到retList中。

具体优化后的代码如下文的【完整代码】

2.4、完整代码

class Solution {public List<List<Integer>> levelOrder(TreeNode root) {List<List<Integer>> retList = new LinkedList<>();if(root == null) {return retList;}Queue<TreeNode> queue = new LinkedList<>();queue.add(root);while(!queue.isEmpty()) {List<Integer> list = new LinkedList<>();   //存放一层节点的集合Listint size = queue.size();   //每次计算队列长度while(size --> 0) {   //每完成一次出队，size自减1TreeNode cur = queue.poll();list.add(cur.val);   if(cur.left != null) {queue.add(cur.left);}if(cur.right != null) {queue.add(cur.right);}}retList.add(list);  //将一层的节点添加到返回集合retList中}return retList;}
}