一、函数
1. 定义
设x与y是两个变量,D是一个给定的数集。若对于每一个x∈D,按照一定的法则f,都有一个确定的值y与之对应,则称y为x的函数,记作y=f(x),称x为自变量,y为因变量,称数集D为此函数的定义域。即当自变量确定时,函数值必须唯一确定。
比如y²=x,一个x对应两个y,所以不是函数
2. 函数的两个性质(重要)
- 一对一的映射关系
成为函数的条件 - 定义域
2.1. 定义域
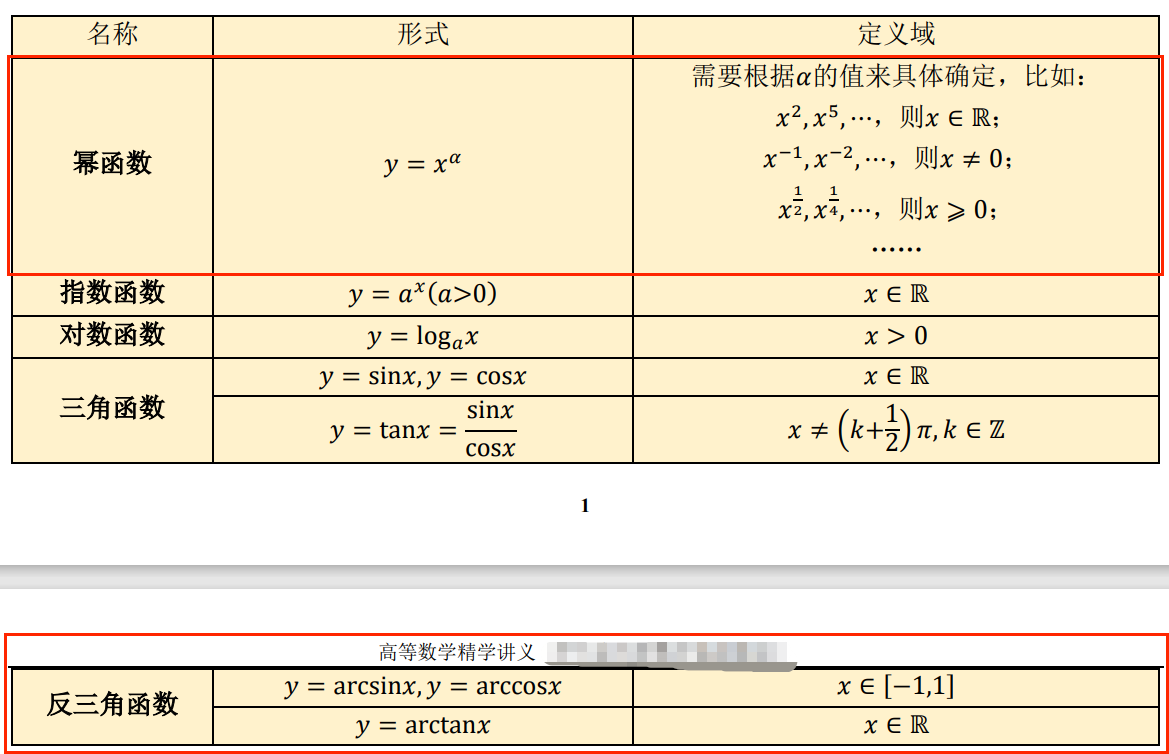
二、反函数
1. 定义
设函数y=f(x)的定义域为D,值域为R 。若对每一个y∈R,都有唯一的x∈D,使得f(x)=y。即一个y对应一个x。以下两点需要说明:

一个函数和反函数之间的曲线是关于直线 y=x 轴对称的。理由:原函数是一个x对应y,反函数则是一个y对应x,很显然(x1,y1)变成(y1,x1)
举例

2. 求反函数的方法
- 在y = f(x)中将y与x互换;
- 重新整理为用x的表达式表示y的格式 。 同时原来的定义域变为新函数的值域,原来的
值域变成新函数的定义域。