算法38：子数组的最小值之和（力扣907题）----单调栈-编程知识

题目：

给定一个整数数组 arr，找到 min(b) 的总和，其中 b 的范围为 arr 的每个（连续）子数组。

示例 1：

输入：arr = [3,1,2,4]
输出：17
解释：
子数组为 [3]，[1]，[2]，[4]，[3,1]，[1,2]，[2,4]，[3,1,2]，[1,2,4]，[3,1,2,4]。 
最小值为 3，1，2，4，1，1，2，1，1，1，和为 17。

示例 2：

输入：arr = [11,81,94,43,3]
输出：444

分析：

很显然，需要分析每个子数组的最小值。而单调栈结构就可以帮助我们找到每个元素左、右侧比自己小的最近位置。也就是说，在一定范围内，数组中每个元素都可以作为子数组的最小值。

假设：

1. 假设数组为1，那么子数组最小值就为1.

2. 假设数组为{1,2} 那么子数组就可以为{1} 和 {1,2}

3. 假设数组为{1,2,3} 那么子数组就可以为{1}、{1，2} 和 {1,2,3}

总结：如果以1为子数组最小值，那么1后面出现的比1大的数，有几个数，子数组就为 n + 1。

数组{1,2,3}中，以1为最小值，那么1后面有2个数比1大，子数组就为 2 + 1 = 3个。

假设数组为{1,2,3}, 现在在最小值1前面加一个数2，变成{2,1,2,3}. 那么子数组就为

{2,1}、{2,1,2} 、{2,1,2,3}

{1}、{1、2}、{1,2,3}

我们发现，子数组数量是原始数组{1,2,3}的2倍，即 2 * 3 = 6 个。

假设，我们在现有的数组中，前面在添加一个元素3. 变成{3,2,1,2,3}. 那么子数组为：

{3,2,1} 、{3,2,1,2} 、{3,2,1,3}

{2,1}、{2,1,2} 、{2,1,2,3}

{1}、{1、2}、{1,2,3}

我们发现，子数组数量是原始数组{1,2,3}的3倍，即 3 * 3 = 9 个.

总结：如果以1为子数组最小值，那么1前面出现的比1大的数，有几个，那么就是（N +1）* 原始个数。

以{3,2,1,2,3}为例子。

如果以1为最小值，1后面有2个数比1大，得到 2+1 = 3； 1前面有2个比1大，得到2+1= 3； 3*3 =9；如果以1为最小值，那么一共有9个子数组。

如果以下标为1的2为最小值，可得（1+1）* (0+1) = 2；即如果以下标为1的2值为最小值，子数组有2个。即 {3,2} 和 {2}

如果以下标为3的位置的2值为最小值，前一个位置为1，即0个。前方0个比自己大的；后面1个3比自己大，可得（0+1）*（1+1） = 2个；即{2}和{2、3}

依次类推，可以得到全部结果.

package code04.单调栈_01;import java.util.Stack;/*** 力扣力扣907题: 子数组的最小值*  https://leetcode.com/problems/sum-of-subarray-minimums/*/
public class Code04_SumOfMinValueInArray {public int sumSubarrayMins(int[] arr){int[][] dp = dp(arr);//long比int能存更长的数据long ans = 0;for (int i = 0; i < arr.length; i++) {//当前数int cur = arr[i];//左侧小于等于当前数的个数int left = i - dp[i][0];//右侧小于等于当前数的个数int right = dp[i][1] - i;ans +=  left * right * (long)cur;ans %= 1000000007;}return (int) ans;}//单调栈，统计出每个位置左、右侧比当前数小的位置public int[][] dp(int[] arr){if(arr == null || arr.length == 0) {return null;}//当前业务需要统计出2列信息, 即左侧比自己小的位置，右侧比自己小的位置int[][] dp = new int[arr.length][2];Stack<Integer> stack = new Stack<>();for (int i = 0; i < arr.length; i++){while (!stack.isEmpty() && arr[stack.peek()] > arr[i]){int cur = stack.pop();// -1代表不存在左侧比cur下标对应的值更小的值int leftIndex = stack.isEmpty() ? -1 : stack.peek();dp[cur][0] = leftIndex;dp[cur][1] = i;}//放入下标stack.push(i);}int rightIndex = arr.length;//栈中剩余元素，保持单调增while (!stack.isEmpty()) {int cur = stack.pop();// -1代表不存在左侧比cur下标对应的值更小的值int leftIndex = stack.isEmpty() ? -1 : stack.peek();dp[cur][0] = leftIndex;//因为单调增、所有右侧不存在比自己还小的值了dp[cur][1] = rightIndex;}return dp;}public static void main(String[] args) {Code04_SumOfMinValueInArray ss = new Code04_SumOfMinValueInArray();int[] aa = {3,1,2,4};System.out.println(ss.sumSubarrayMins(aa));}
}

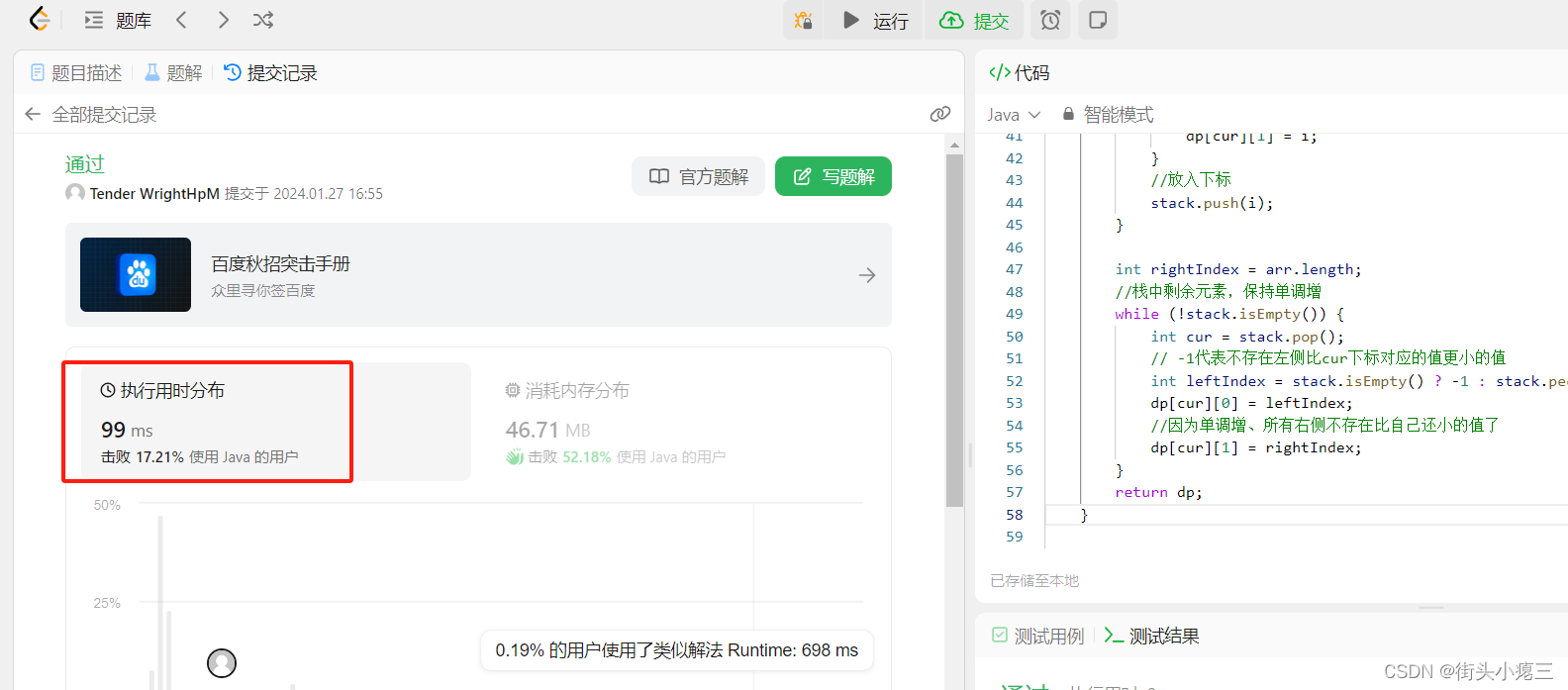
虽然测试通过了，但是执行用时99ms，只击败了17%的用户，说明代码不够优秀。

技巧就是，将java原有的Stack替换成自己实现的数组。因为自己实现的数组是固定的，而Stack是需要不断经过扩容的。这样优化，效果很明显。

package code04.单调栈_01;import java.util.Stack;/*** 力扣力扣907题: 子数组的最小值*  https://leetcode.com/problems/sum-of-subarray-minimums/*/
public class Code04_SumOfMinValueInArray_opt {public int sumSubarrayMins(int[] arr){int[][] dp = dp(arr);//long比int能存更长的数据long ans = 0;for (int i = 0; i < arr.length; i++) {//当前数int cur = arr[i];//左侧小于等于当前数的个数int left = i - dp[i][0];//右侧小于等于当前数的个数int right = dp[i][1] - i;ans +=  left * right * (long)cur;ans %= 1000000007;}return (int) ans;}//单调栈，统计出每个位置左、右侧比当前数小的位置public int[][] dp(int[] arr){if(arr == null || arr.length == 0) {return null;}//当前业务需要统计出2列信息, 即左侧比自己小的位置，右侧比自己小的位置int[][] dp = new int[arr.length][2];int[] stack = new int[arr.length];int stackSize = 0;for (int i = 0; i < arr.length; i++){while (stackSize != 0 && arr[stack[stackSize-1]] > arr[i]){int cur = stack[--stackSize];// -1代表不存在左侧比cur下标对应的值更小的值int leftIndex = stackSize == 0 ? -1 : stack[stackSize - 1];dp[cur][0] = leftIndex;dp[cur][1] = i;}//放入下标stack[stackSize++] = i;}int rightIndex = arr.length;//栈中剩余元素，保持单调增while (stackSize != 0) {int cur = stack[--stackSize];// -1代表不存在左侧比cur下标对应的值更小的值int leftIndex = stackSize == 0 ? -1 : stack[stackSize - 1];dp[cur][0] = leftIndex;//因为单调增、所有右侧不存在比自己还小的值了dp[cur][1] = rightIndex;}return dp;}public static void main(String[] args) {Code04_SumOfMinValueInArray_opt ss = new Code04_SumOfMinValueInArray_opt();int[] aa = {3,1,2,4};int[][] dp = ss.dp(aa);for (int i = 0; i < dp.length; i++) {System.out.println("当前下标 ：" + i + ", 左侧小值: " + dp[i][0] + ", 右侧小值： " + dp[i][1]);}System.out.println(ss.sumSubarrayMins(aa));}
}

优化完以后，效果很明显：