OD统一考试(C卷)
分值: 200分
题解: Java / Python / C++

题目描述
给定两个字符串,分别为字符串A与字符串B。
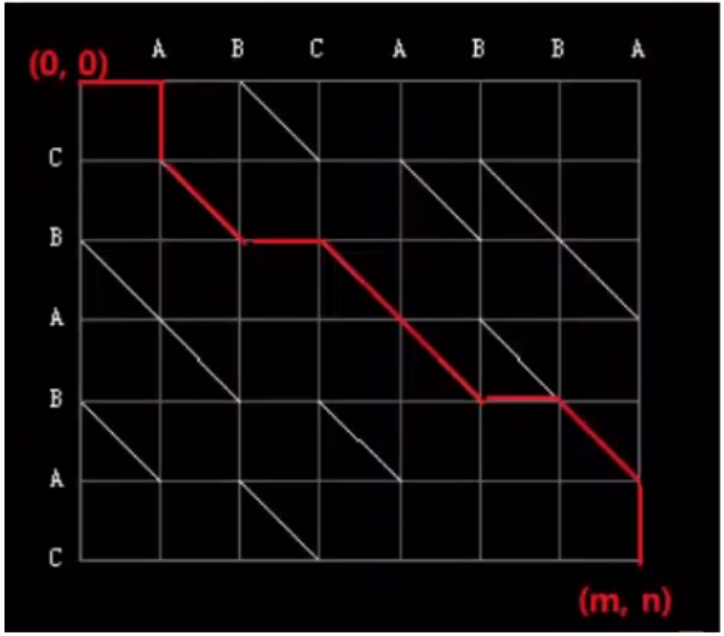
例如A字符串为ABCABBA,B字符串为CBABAC可以得到下图m*n的二维数组,定义原点为(0, 0),终点为(m, n),水平与垂直的每一条边距离为1,映射成坐标系如下图。
从原点(0, 0)到(0, A)为水平边,距离为1,从(0, A)到(A, C)为垂直边,距离为1;
假设两个字符串同一位置的两个字符相同则可以作一个斜边,如(A, C)到(B, B)最短距离为斜边,距离同样为1。
作出所有的斜边如下图,(0, 0)到(B, B)的距离为 1个水平边 + 1个垂直边 + 1个斜边 = 3。

根据定义可知,原点到终点的最短距离路径如下图红线标记,最短距离为:9
输入描述
空格分割的两个字符串A与字符串B,字符串不为“空串”,字符格式满足正则规则:[A-Z],字符串长度<10000
输出描述
原点到终点的最短距离
示例1
输入:
ABC ABC输出:
3
示例2
输入:
ABCABBA CBABAC输出:
9
题解
这是一道典型的动态规划题目。题目要求计算两个字符串之间的最短距离,规定了三种操作:水平边移动、垂直边移动和斜边移动。每一种操作的距离为1。
解题思路
我们可以使用动态规划来解决这个问题。我们可以定义一个二维数组
dp,其中dp[r][c]表示从原点到(r, c)点的最短距离。然后,我们可以根据题目规定的操作来更新dp数组。具体步骤如下:
- 初始化
dp数组,将所有元素初始化为一个较大的值(表示无穷大),除了dp[0][0]初始化为0。- 初始化边界条件,即从原点到第一行和第一列的最短距离。
- 使用双层循环遍历字符串A和B的每个字符,根据题目规定的操作更新
dp数组。操作包括水平边移动、垂直边移动和斜边移动。- 最终,
dp[m][n]即为从原点到终点的最短距离。
Java
import java.util.Arrays;
import java.util.Scanner;/*** @author code5bug*/
public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);String A = scanner.next(), B = scanner.next();int m = A.length(), n = B.length();// dp[r][c] 为从原点到 (r,c)点的最短距离int[][] dp = new int[m + 1][n + 1];for (int r = 0; r <= n; r++) Arrays.fill(dp[r], Integer.MAX_VALUE);dp[0][0] = 0;for (int r = 0; r < m; r++) dp[r + 1][0] = dp[r][0] + 1;for (int c = 0; c < n; c++) dp[0][c + 1] = dp[0][c] + 1;for (int r = 0; r < m; r++) {for (int c = 0; c < n; c++) {// 来自从左侧 或 上侧dp[r + 1][c + 1] = Math.min(dp[r][c + 1], dp[r + 1][c]) + 1;if (A.charAt(r) == B.charAt(c)) { // 来自从左上角dp[r + 1][c + 1] = Math.min(dp[r + 1][c + 1], dp[r][c] + 1);}}}System.out.println(dp[m][n]);}
}Python
from math import inf
A, B = input().split()
cols, rows = len(A), len(B)# dp[r][c] 为从原点到 (r,c)点的最短距离
dp = [[inf] * (cols + 1) for _ in range(rows + 1)]# 初始化边界
dp[0][0] = 0for r in range(0, rows):dp[r+1][0] = dp[r][0] + 1
for c in range(0, cols):dp[0][c+1] = dp[0][c] + 1for r in range(rows):for c in range(cols):dp[r+1][c+1] = min(dp[r+1][c], dp[r][c+1]) + 1if A[c] == B[r]:dp[r+1][c+1] = min(dp[r+1][c+1], dp[r][c] + 1)print(dp[rows][cols])
# Python3 AC 96
# PyPy3 AC 100
C++
#include <iostream>
#include <vector>
#include <algorithm>using namespace std;int main() {string A, B;cin >> A >> B;int m = A.length(), n = B.length();// dp[r][c] 为从原点到(r,c)点的最短距离vector<vector<int>> dp(m + 1, vector<int>(n + 1, INT_MAX));dp[0][0] = 0;for (int r = 0; r < m; r++)dp[r + 1][0] = dp[r][0] + 1;for (int c = 0; c < n; c++)dp[0][c + 1] = dp[0][c] + 1;for (int r = 0; r < m; r++) {for (int c = 0; c < n; c++) {// 来自从左侧或上侧dp[r + 1][c + 1] = min(dp[r][c + 1], dp[r + 1][c]) + 1;if (A[r] == B[c]) { // 来自从左上角dp[r + 1][c + 1] = min(dp[r + 1][c + 1], dp[r][c] + 1);}}}cout << dp[m][n] << endl;return 0;
}相关练习题
| 题号 | 题目 | 难易 |
|---|---|---|
| LeetCode LCR 099 | LCR 099. 最小路径和 | 中等 |
| LeetCode 61 | 64. 最小路径和 | 中等 |
❤️华为OD机试面试交流群(每日真题分享): 加V时备注“华为od加群”
🙏整理题解不易, 如果有帮助到您,请给点个赞 ❤️ 和收藏 ⭐,让更多的人看到。🙏🙏🙏