第六部分、数据结构树,树存储结构详解

数据结构的树存储结构,常用于存储逻辑关系为 "一对多" 的数据。
树存储结构中,最常用的还是二叉树,本章就二叉树的存储结构、二叉树的前序、中序、后序以及层次遍历、线索二叉树、哈夫曼树等,详细介绍二叉树。
树是数据结构中的重点,同时更是难点,没有捷径,需要初学者静下心,死扣各个知识点。
十一、什么是栈,栈存储结构详解
通过前一节对线索二叉树的学习,其中,在遍历使用中序序列创建的线索二叉树时,对于其中的每个结点,即使没有线索的帮助下,也可以通过中序遍历的规律找到直接前趋和直接后继结点的位置。
也就是说,建立的线索二叉链表可以从两个方向对结点进行中序遍历。通过前一节的学习,线索二叉链表可以从第一个结点往后逐个遍历。但是起初由于没有记录中序序列中最后一个结点的位置,所以不能实现从最后一个结点往前逐个遍历。
双向线索链表的作用就是可以让线索二叉树从两个方向实现遍历。
1、双向线索二叉树的实现过程
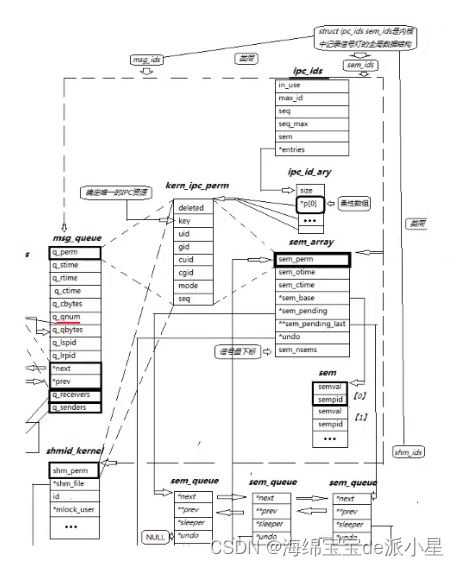
在线索二叉树的基础上,额外添加一个结点。此结点的作用类似于链表中的头指针,数据域不起作用,只利用两个指针域(由于都是指针,标志域都为 0 )。
左指针域指向二叉树的树根,确保可以正方向对二叉树进行遍历;同时,右指针指向线索二叉树形成的线性序列中的最后一个结点。
这样,二叉树中的线索链表就变成了双向线索链表,既可以从第一个结点通过不断地找后继结点进行遍历,也可以从最后一个结点通过不断找前趋结点进行遍历。
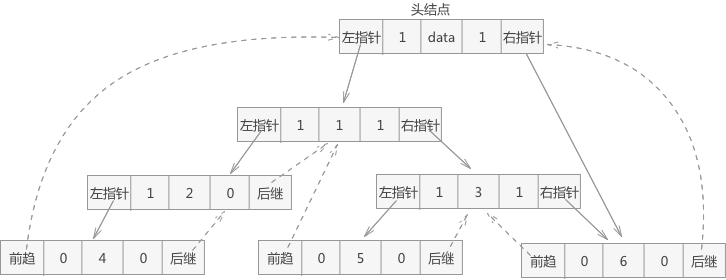
图1 双向线索二叉链表
代码实现:
//建立双向线索链表
void InOrderThread_Head(BiThrTree *h, BiThrTree t)
{
//初始化头结点
(*h) = (BiThrTree)malloc(sizeof(BiThrNode));
if((*h) == NULL){
printf("申请内存失败");
return ;
}
(*h)->rchild = *h;
(*h)->Rtag = Link;
//如果树本身是空树
if(!t){
(*h)->lchild = *h;
(*h)->Ltag = Link;
}
else{
pre = *h;//pre指向头结点
(*h)->lchild = t;//头结点左孩子设为树根结点
(*h)->Ltag = Link;
InThreading(t);//线索化二叉树,pre结点作为全局变量,线索化结束后,pre结点指向中序序列中最后一个结点
pre->rchild = *h;
pre->Rtag = Thread;
(*h)->rchild = pre;
}
}
2、双向线索二叉树的遍历
双向线索二叉树遍历时,如果正向遍历,就从树的根结点开始。整个遍历过程结束的标志是:当从头结点出发,遍历回头结点时,表示遍历结束。
//中序正向遍历双向线索二叉树
void InOrderThraverse_Thr(BiThrTree h)
{
BiThrTree p;
p = h->lchild; //p指向根结点
while(p != h)
{
while(p->Ltag == Link) //当ltag = 0时循环到中序序列的第一个结点
{
p = p->lchild;
}
printf("%c ", p->data); //显示结点数据,可以更改为其他对结点的操作
while(p->Rtag == Thread && p->rchild != h)
{
p = p->rchild;
printf("%c ", p->data);
}
p = p->rchild; //p进入其右子树
}
}
逆向遍历线索二叉树的过程即从头结点的右指针指向的结点出发,逐个寻找直接前趋结点,结束标志同正向遍历一样:
//中序逆方向遍历线索二叉树
void InOrderThraverse_Thr(BiThrTree h){
BiThrTree p;
p=h->rchild;
while (p!=h) {
while (p->Rtag==Link) {
p=p->rchild;
}
printf("%c",p->data);
//如果lchild为线索,直接使用,输出
while (p->Ltag==Thread && p->lchild !=h) {
p=p->lchild;
printf("%c",p->data);
}
p=p->lchild;
}
}
3、完整代码实现
#include <stdio.h>
#include <stdlib.h>
#define TElemType char//宏定义,结点中数据域的类型
//枚举,Link为0,Thread为1
typedef enum {
Link,
Thread
}PointerTag;
//结点结构构造
typedef struct BiThrNode {
TElemType data;//数据域
struct BiThrNode* lchild, *rchild;//左孩子,右孩子指针域
PointerTag Ltag, Rtag;//标志域,枚举类型
}BiThrNode, *BiThrTree;
BiThrTree pre = NULL;
//采用前序初始化二叉树
//中序和后序只需改变赋值语句的位置即可
void CreateTree(BiThrTree * tree) {
char data;
scanf("%c", &data);
if (data != '#') {
if (!((*tree) = (BiThrNode*)malloc(sizeof(BiThrNode)))) {
printf("申请结点空间失败");
return;
}
else {
(*tree)->data = data;//采用前序遍历方式初始化二叉树
(*tree)->Ltag = Link;
(*tree)->Rtag = Link;
CreateTree(&((*tree)->lchild));//初始化左子树
CreateTree(&((*tree)->rchild));//初始化右子树
}
}
else {
*tree = NULL;
}
}
//中序对二叉树进行线索化
void InThreading(BiThrTree p) {
//如果当前结点存在
if (p) {
InThreading(p->lchild);//递归当前结点的左子树,进行线索化
//如果当前结点没有左孩子,左标志位设为1,左指针域指向上一结点 pre
if (!p->lchild) {
p->Ltag = Thread;
p->lchild = pre;
}
//如果 pre 没有右孩子,右标志位设为 1,右指针域指向当前结点。
if (pre && !pre->rchild) {
pre->Rtag = Thread;
pre->rchild = p;
}
pre = p;//pre指向当前结点
InThreading(p->rchild);//递归右子树进行线索化
}
}
//建立双向线索链表
void InOrderThread_Head(BiThrTree *h, BiThrTree t)
{
//初始化头结点
(*h) = (BiThrTree)malloc(sizeof(BiThrNode));
if ((*h) == NULL) {
printf("申请内存失败");
return;
}
(*h)->rchild = *h;
(*h)->Rtag = Link;
//如果树本身是空树
if (!t) {
(*h)->lchild = *h;
(*h)->Ltag = Link;
}
else {
pre = *h;//pre指向头结点
(*h)->lchild = t;//头结点左孩子设为树根结点
(*h)->Ltag = Link;
InThreading(t);//线索化二叉树,pre结点作为全局变量,线索化结束后,pre结点指向中序序列中最后一个结点
pre->rchild = *h;
pre->Rtag = Thread;
(*h)->rchild = pre;
}
}
//中序正向遍历双向线索二叉树
void InOrderThraverse_Thr(BiThrTree h)
{
BiThrTree p;
p = h->lchild; //p指向根结点
while (p != h)
{
while (p->Ltag == Link) //当ltag = 0时循环到中序序列的第一个结点
{
p = p->lchild;
}
printf("%c ", p->data); //显示结点数据,可以更改为其他对结点的操作
while (p->Rtag == Thread && p->rchild != h)
{
p = p->rchild;
printf("%c ", p->data);
}
p = p->rchild; //p进入其右子树
}
}
int main() {
BiThrTree t;
BiThrTree h;
printf("输入前序二叉树:\n");
CreateTree(&t);
InOrderThread_Head(&h, t);
printf("输出中序序列:\n");
InOrderThraverse_Thr(h);
return 0;
}
运行结果:
输入前序二叉树:
124###35##6##
输出中序序列:
4 2 1 5 3 6
程序中只调用了正向遍历线索二叉树的代码,如果逆向遍历,直接替换逆向遍历的函数代码到程序中即可。
十二、树的双亲表示法(包含C语言实现代码)
前面讲了二叉树的顺序存储和链式存储,本节来学习如何存储具有普通树结构的数据。
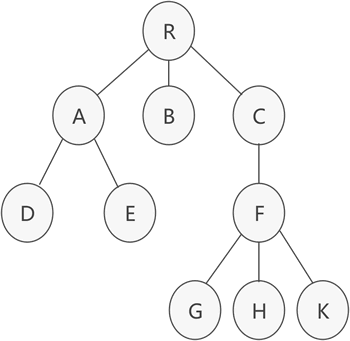
图 1 普通树存储结构
如图 1 所示,这是一棵普通的树,该如何存储呢?通常,存储具有普通树结构数据的方法有 3 种:
- 双亲表示法;
- 孩子表示法;
- 孩子兄弟表示法;
本节先来学习双亲表示法。
双亲表示法采用顺序表(也就是数组)存储普通树,其实现的核心思想是:顺序存储各个节点的同时,给各节点附加一个记录其父节点位置的变量。
注意,根节点没有父节点(父节点又称为双亲节点),因此根节点记录父节点位置的变量通常置为 -1。
例如,采用双亲表示法存储图 1 中普通树,其存储状态如图 2 所示:
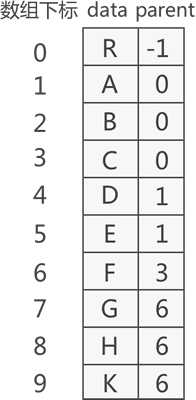
图 2 双亲表示法存储普通树示意图
图 2 存储普通树的过程转化为 C 语言代码为:
#define MAX_SIZE 100//宏定义树中结点的最大数量
typedef char ElemType;//宏定义树结构中数据类型
typedef struct Snode{
TElemType data;//树中结点的数据类型
int parent;//结点的父结点在数组中的位置下标
}PTNode;
typedef struct {
PTNode tnode[MAX_SIZE];//存放树中所有结点
int n;//根的位置下标和结点数
}PTree;
因此,存储图 1 中普通树的 C 语言实现代码为:
#include<stdio.h>
#include<stdlib.h>
#define MAX_SIZE 20
typedef char ElemType;//宏定义树结构中数据类型
typedef struct Snode //结点结构
{
ElemType data;
int parent;
}PNode;
typedef struct //树结构
{
PNode tnode[MAX_SIZE];
int n; //结点个数
}PTree;
PTree InitPNode(PTree tree)
{
int i, j;
char ch;
printf("请输出节点个数:\n");
scanf("%d", &(tree.n));
printf("请输入结点的值其双亲位于数组中的位置下标:\n");
for (i = 0; i < tree.n; i++)
{
getchar();
scanf("%c %d", &ch, &j);
tree.tnode[i].data = ch;
tree.tnode[i].parent = j;
}
return tree;
}
void FindParent(PTree tree)
{
char a;
int isfind = 0;
printf("请输入要查询的结点值:\n");
getchar();
scanf("%c", &a);
for (int i = 0; i < tree.n; i++) {
if (tree.tnode[i].data == a) {
isfind = 1;
int ad = tree.tnode[i].parent;
printf("%c的父节点为 %c,存储位置下标为 %d", a, tree.tnode[ad].data, ad);
break;
}
}
if (isfind == 0) {
printf("树中无此节点");
}
}
int main()
{
PTree tree;
for (int i = 0; i < MAX_SIZE; i++) {
tree.tnode[i].data = " ";
tree.tnode[i].parent = 0;
}
tree = InitPNode(tree);
FindParent(tree);
return 0;
}
程序运行示例:
请输出节点个数:
10
请输入结点的值其双亲位于数组中的位置下标:
R -1
A 0
B 0
C 0
D 1
E 1
F 3
G 6
H 6
K 6
请输入要查询的结点值:
C
C的父节点为 R,存储位置下标为 0




![[Grafana]ES数据源Alert告警发送](https://img-blog.csdnimg.cn/direct/ed9b6dd33dcf4a338f57901498de61e9.png)